Польза и вред эллиптических тренажеров для здоровья
Статья
04 августа 2022
Содержание
- Чем полезен эллиптический тренажер
- Минусы орбитрека
- На что ещё обратить внимание при покупке эллиптического тренажёра?
- Что важно учитывать, чтобы добиться максимального эффекта?
О пользе и вреде эллиптического тренажёра написано немало, в том числе и откровенной ерунды. Давайте же разберёмся, в чём действительно плюсы и минусы как самого спортивного оборудования, так и эффекта, который он даёт тем, кто на нём занимается.
Чем полезен эллиптический тренажер
-
Прежде всего, он способен заменить много другого оборудования, тем самым сэкономить и ваш бюджет, и пространство в квартире. При этом вы всё же получите и подтянутое тело, и улучшение самочувствия довольно скоро после начала тренировок.
Ну и ещё он довольно компактен, поэтому не будет загромождать пространство даже в небольших современных квартирах.
-
Эллиптический тренажёр — находка для желающих не только избавиться от лишних килограммов, но и избежать негативного эффекта от резкого похудения, например, обвисшей, дряблой кожи, «апельсиновой корки» на бёдрах. Всё дело в том, что во время тренировке на таком оборудовании у вас будут работать большинство мышц, что позволит вам убирать лишние сантиметры со всего тела равномерно.
-
За счёт работы со многими группами мышц достигается и ещё один положительный эффект — нагрузка на суставы, позвоночный столб в целом и каждый позвонок в частности. Поэтому он допустим для людей с проблемными суставами, варикозным расширением вен.
-
Во время занятий на эллипсоиде вы укрепляете многие системы организма, в том числе, дыхательную, кровеносную, сосудистую и расслабляете нервную систему, поскольку, в отличие от беговых дорожек, вам не надо будет следить за тем, правильно ли вы ставите ногу, не упадёте ли с неё.
С ним можно не задумываться о своей безопасности и всецело отдаться процессу тренировки. -
Тренировки на эллиптическом тренажёре настолько эффективны, что помимо работы с мышцами работают ещё и на ускорение метаболизма. А это означает, что сжигать калории ваш организм будет даже некоторое время после того, как вы уже закончите спортивные занятия.
-
Кроме того, современные модели оснащены и дополнительным функциями: вы можете следить за частотой пульса, посмотреть на скорость, с которой идёте или бежите, уточнить, какое количество калорий ваш организм уже сжёг, а ещё выставить отдельные программы для интервальной тренировки или интенсивного сжигания жира.
-
Поразительно, но при всех своих преимуществах такие тренажёры довольно доступны по цене. Безусловно, всё зависит от конкретной модели, производителя, набора дополнительных функций. Но в целом позволить себе такой спортивный агрегат могут очень многие.
Ну и ещё он довольно компактен, поэтому не будет загромождать пространство даже в небольших современных квартирах.
Минусы орбитрека
При всех очевидных плюсах, нельзя не сказать и о некоторых недостатках эллиптических тренажёров. Чаще всего отмечают то, что они не настолько эффективны для верхней части корпуса. Как ни старайтесь, но накачать руки и плечи на нём вы не сможете. Но здоровья всё равно прибавится. Силовые тренировки на эллипсоидах под силу только уже уверенным спортсменам, совсем новичкам поддерживать высокий темп долго едва ли получится. Но с чего-то надо начинать.
Некоторые пеняют на монотонность занятий. Но это дело вкуса. Кому-то хочется провести эффективную тренировку и освободить голову для других мыслей или просто послушать музыку, ни о чём не думая, просто повторяя одни и те же движения, которые при этом приведут к потрясающим результатам.
Необходимость выбирать тренажёр под габариты того, кто будет заниматься. Да, это верно. При покупке эллипсоида важно учитывать рост и вес тех, кто будет его использовать.
Но тут всё довольно просто: если вы хотите приобрести орбитрек для всей семьи, просто учитывайте вес самого тяжёлого родственника. Ещё лучше брать оборудование с запасом грузоподъёмности. Хотя бы небольшой, + 20%. Например, если весь главы семьи (самого тяжёлого спортсмена) равен 112 кг, то расчёт делается так: 112 + 112*0,2 = 134,4 килограмма. Округлите и получится, что вам нужно оборудование с грузоподъёмностью в 135 килограммов. Так вы точно не ошибётесь и эллипсоид не сломается через неделю от непомерных нагрузок.
Чтобы угадать с ростом, то тут тоже есть довольно простая формула. От роста зависит длина шага. Люди не выше 165 см обычно имеют длину шага в 40 сантиметров, от 165 до 180 см — 50 см, те, кто выше 1,8 метра при ходьбе за один шаг преодолевают более 50 сантиметров. Поэтому, чтобы тренировки были эффективные, а ваш организм не испытывал дополнительного неудобства, обязательно учитывайте эти параметры.
На что ещё обратить внимание при покупке эллиптического тренажёра?
Когда вы уже определились с тем, какой грузоподъёмностью и шириной шага должен обладать ваш эллиптический тренажёр, не забудьте уточнить, какой тип привода в выбранной вами модели.
Они бывают механическими, магнитными, электромагнитными. Правда, механический тип вы скорее всего не найдёте, а если «повезёт», то лучше откажитесь от такой покупки, поскольку тренажёры с таким типом привода довольно шумные, да и функциональность у них невысока. Зато другие варианты — вполне подойдут! Они тихо работают, имеют мягкий ход, не занимают много места, обладают дополнительным функциями и очень эффективны.
Не лишним будет определиться и с габаритами будущей покупки. Мы уже писали, что в целом эллипсоиды довольно компактны, но всё же, если вы счастливый обладатель большой квартиры, не скупитесь на приобретение полноразмерных моделей, в который маховик расположен сзади. Если же дорог каждый сантиметр свободного пространства современных квартир или студий, то ваш вариант с расположением маховика спереди, ещё лучше, если вы найдёте складывающуюся модель.
Что важно учитывать, чтобы добиться максимального эффекта?
Прежде всего не забывайте, что покупка орбитрека не сделает вас автоматически подтянутым и здоровым.
Обращайте внимание на положение тела и правильность выполнения тренировки: ваши стопы должны уверено стоять на педалях. Следите за тем, что ни пятка, ни носок не отрывались во время движения, вы увеличите нагрузку на суставы и не добьётесь положительного эффекта. Избегайте порывистых движений, ваше дыхание должно быть ровным, глубоким.
Чередуйте режимы. Позанимались какое-то время — отдохните! Это базовый принцип эффективных аэробных тренировок. По этой же причине старайтесь использовать разные программы, так мышцы не привыкнут к одному и тому же занятию, а занятия будут интереснее и полезнее. Начинайте тренировку с разминки.
Новости и аналитика в реальном времени
Профессиональные фитнес-инструкторы советуют приобрести эллипсоид для домашнего спортзала.
Чем полезен эллиптический тренажер?
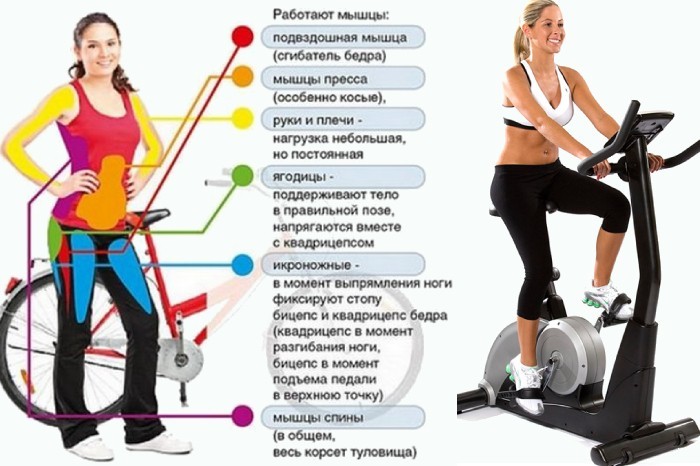
Эллипсоид представляет собой конструкцию из степпера с поручнями для рук. Простая тренировка позволяет задействовать как верхнюю часть тела (бицепсы, плечи, грудь и трицепсы), так и нижнюю (подколенные сухожилия, икры, четырехглавые мышцы, ягодицы). Также могут быть задействованы мышцы живота и спины. Главное держать осанку, правильно подбирать нагрузку.
Занятия на эллиптических тренажерах укрепляют здоровье, помогают поддерживать фигуру в тонусе.
Даже 2-3 тренировки в неделю позволят ощутить на себе следующие преимущества.
Выбирайте только оригинальные эллиптические тренажеры от официальных дилеров, каким является интернет-магазин Спортмаркет: https://sportmarket.net.ua/orbitreki/ здесь вы можете заказать качественный эллипс с доставкой.
1. Активизация кровообращения.
Двигательная активность способствует улучшению кровотока. Кровь, в свою очередь, обеспечивает поставку кислорода ко всем частям тела. Оксигенация снижает риск развития сезонных респираторных заболеваний. Хорошая циркуляция крови поддерживает работоспособность жизненно важных органов и даже помогает улучшить качество сна.
2. Повышение выносливости.
Высокоинтенсивная пятнадцатиминутная тренировка с максимальной нагрузкой или простое тридцатиминутное занятие увеличит выносливость сердечной мышцы. Если тренироваться ежедневно, то уже через неделю можно будет увидеть снижение пульса. ЧСС — главный показатель выносливости организма.
3.
Сохранение здоровья коленных суставов.
Во время классического бега нагрузка переносится на колени, лодыжки или бедра. При использовании эллипсоида, вес можно перенести на руки.
Кардиотренировка позволит накачивать мышцы, развивать сердечно-сосудистую систему без износа суставов.
Оценить пользу эллиптического тренажера можно только в случае регулярных тренировок. Единичные занятия не позволят достичь желаемых результатов.
Фитнес-инструкторы рекомендуют использовать его не менее 150 минут в неделю.
Эффект от эллиптического тренажера для здоровья и внешности
Современные эллипсоиды укомплектованы компьютером. Спортсмен может выбрать запрограммированную тренировку, которая будет имитировать восхождение на гору, легкую городскую прогулку. Также можно самостоятельно выбирать нагрузку, время занятий.
После серии регулярных тренировок на эллипсе, можно будет заметить позитивные изменения в фигуре. Простые упражнения способствуют:
- сжиганию калорий;
- устранению жировых отложений;
- тонизированию мышц.
Максимального эффекта можно достичь, практикуя интервальные тренировки. Фитнес-инструкторы рекомендуют работать по схеме: 3 минуты интенсивной работы на высокой скорости с низкой нагрузкой чередовать с минутой «отдыха» на низкой скорости с высокой нагрузкой.
Еще один положительный эффект: укрепление специфических мышц ног.
Регулируя угол наклона педалей профессионального эллипсоидного тренажера (https://sportmarket.net.ua/professionalnye-orbitreki/), можно укрепить икры, мелкие камбаловидные мышцы, которые не задействуются во время выполнения других упражнений. При занятиях «задним ходом» также можно проработать подколенные сухожилия, ягодицы.
Кроме видимого эффекта для фигуры, занятия на эллипсоиде способствуют улучшению координации. Продвинутые спортсмены настолько хорошо владеют своим телом, что занимаются на эллипсоиде, не придерживаясь за поручни.
Недостатки и возможный вред эллиптического тренажера
При правильной технике выполнения упражнений, занятия на нем не будут вредны для здоровья.
К недостаткам эллипсоида можно отнести низкую интенсивность тренировок. Даже если выбрать максимальную нагрузку, для достижения видимого эффекта нужно будет заниматься в 2-3 раза дольше, чем на беговой дорожке или велотренажере. Чтобы избежать возможного вреда от неправильного выполнения упражнений, рекомендуется проконсультироваться с профессиональным фитнес-инструктором перед началом занятий.
Эллипсоиды считаются самыми безопасными тренажерами. Он остается оптимальным выбором для домашнего спортзала.
[lampps-users] Моделирование эллипсоидов с диполями — Зеркало списка рассылки LAMMPS
lampmps-users
#1
Я пытаюсь выполнить NVT-моделирование эллиптических частиц с прикрепленными к ним диполями со смещенными точками. Я прилагаю файл данных и входной файл LAMMPS.
Я использовал гибрид atom_style. Использовались 2 типа частиц (эллипсоид без диполя и точечная частица с точечным диполем) и использовались фиксированные жесткие, чтобы рассматривать их как отдельные частицы. Нужно знать, правильно я делаю или нет.
ТИА.
ellipse_dipole.dat (306 КБ)
in.ellipse (1,89 КБ)
jewettaij
#2
Это имеет смысл. Я не думаю, что код для «фиксировать жесткость» понимает
неточечных частиц (эллипсов, диполей). Я не знаю другого способа
выполнить то, что вы пытаетесь сделать, используя официальный код
Самые продвинутые модели с использованием эллипсоидов в LAMMPS
реализован с использованием кода «MOLC», разработанного Маттео Риччи и
Оттелло Росциони.
Он делает что-то очень похожее на то, что вы пытаетесь сделать
. Написанная ими статья включает их код LAMMPS, но
в их коде отсутствует документация. Бумага здесь.
МОК. Обратимый крупнозернистый подход с использованием анизотропных шариков для…
Мы описываем разработку и внедрение крупнозернистого (CG) подхода к моделированию, при котором сложные органические молекулы, и особенно молекулы с π-сопряжением, часто используемые в органической электронике, моделируются в терминах связанных наборов…
Они не отказались от этого. Если вы отправите письмо Отелло по электронной почте, он, вероятно,
захочет помочь вам использовать их код, потому что они хотят продвигать
этот метод.
Если вы прочтете их статью, она, вероятно, вас смутит, поскольку в ней
в крупнозернистые эллипсоидальные молекулы. К счастью
, их код является общим и работает для всех эллипсоидальных симуляций.
Вы, , можете использовать их код LAMMPS, не следуя их сложным
крупнозернистая процедура. Несколько парных стилей (а также бондовых стилей)
были созданы для того, чтобы сделать возможными
такого рода симуляции. Но код еще не отправлен для включения в дистрибутив
LAMMPS. (Думаю, Маттео увяз в написании документации по
, и этого так и не произошло.)
Файлы с исходным кодом имеют следующие имена:0009 pare_coul_cut_offcentre.h
pair_coul_long_offcentre.cpp
pair_coul_long_offcentre.h
pppm_offcentre.cpp
pppm_offcentre.h
… и название
Bond_style lllipsoid
. kspace_style pppm/offcentre
Вам потребуется загрузить исходный код LAMMPS, скопировать эти файлы
в подкаталог «src/» и перекомпилировать LAMMPS.
В своих симуляциях вы, вероятно, захотите использовать что-то вроде:
pair_style hybrid/overlay gayberne 1.0 1.0 -3.0 14.
coul/long/offcentre 14. 4 &
kspace_style pppm/offcentre 1e-4 4 &
К сожалению, я подозреваю, что их код, вероятно, не скомпилируется, потому что
были некоторые изменения в LAMMPS с тех пор, как вышла их статья.
(Синтаксис функций «numeric()» и «inumeric()»
изменился.) Если вы не можете понять, как заставить LAMMPS компилироваться, тогда
существует старая версия LAMMPS, которая включает их код и
.0009 компилируется. Он находится здесь.
Несколько расширенных примеров moltemplate и код, необходимый для их запуска
Набор файлов для демонстрации некоторых расширенных функций программного обеспечения moltemplate для крупнозернистого построения молекул для LAMMPS (moltemplate.org). Эти файлы намеренно усложнены, чтобы показать…
Вам нужно будет загрузить второй файл архива, распаковать подкаталог LAMMPS
и скомпилировать эту версию LAMMPS.
В качестве альтернативы вы можете попробовать отправить по электронной почте Otello для получения последней версии исходного кода.
По ссылке выше также есть пример, который демонстрирует, как
запускать подобные эллипсоидальные симуляции. К сожалению, это не простой пример
.
Требуется установка «moltemplate» для создания файлов данных
LAMMPS и входных сценариев, необходимых для запуска примера. Вы
должны скачать первый файл архива по ссылке выше и
распаковать его. Пример находится в каталоге с именем
«дополнительная_фигура_6_эллипсоидальный_бифенил».
Кстати, этот пример является частью статьи
(https://doi.org/10.1016/j.jmb.2021.166841). Я могу отправить его вам, если
у вас нет доступа к легкой загрузке.
— ВИЗУАЛИЗИРУЙТЕ свои результаты —
Независимо от того, как вы реализуете эту симуляцию (используя фиксированную жесткость или используя
новый код «MOLC» от Маттео и Отелло), вы должны визуализировать свою траекторию
. Это первое, что вы должны попробовать, когда дела
не работает.
Я провел короткую симуляцию, используя модифицированную версию вашего файла in.ellipse
(прилагается), и визуализировал файл траектории с помощью OVITO.
Хотя расстояние между двумя частицами остается прежним,
ориентации эллипсоида и диполя могут свободно вращаться.
Это
, вероятно, не то, что вы хотели, и это легко объясняет, почему энергия
не сохраняется, а ваша температура увеличивается. (Возможно,
-точечные диполи располагались слишком близко друг к другу. Мне 9 лет.0009 удивило, что симуляция не дала сбой.)
Чтобы визуализировать ваши файлы траекторий, я думаю, вам нужно создать файл одной траектории
, содержащий как эллипсоидную, так и дипольную
ориентацию. (См. прикрепленный файл «in.ellipsoid».) Затем отобразите
степеней свободы диполя и эллипсоида. Затем выберите две из
частиц, которые являются частью одной и той же молекулы. Затем добавьте модификацию
«Инвертировать выделение». Затем добавьте модификацию «удалить
выбранных частиц».
в.эллипс (2,13 КБ)
akohlmey
#3
это утверждение неверно, в чем легко убедиться, взглянув на исходный код.
вы увидите, что для твердых тел как сила на частицу, так и крутящий момент на частицу учитываются во время функций initial_integrate() и final_integrate()
и что эллипсоиды и сфероиды (но не точечные диполи) имеют дополнительные степени свободы, которые удалены от система в функции dof().
ось.
еветтайдж
#4
Это имеет смысл. Я не думаю, что код для «фиксировать жесткость» понимает
неточечных частиц (эллипсов, диполей).это утверждение неверно, в чем легко убедиться, просмотрев исходный код.
вы увидите, что для твердых тел как сила на частицу, так и крутящий момент на частицу учитываются во время функций initial_integrate() и final_integrate()
и что эллипсоиды и сфероиды (но не точечные диполи) имеют дополнительные степени свободы, которые удаляются из системы в функции dof().
ось.
Приятно знать. Soumik использует эту команду для интеграции
уравнений движения:
fixfixrigid all hard/nvt/small molecule temp 2.0 2.0 0.1
Я не проверял исходный код. Но что бы это ни стоило, когда я запустил
его симуляцию и попытался посмотреть на траекторию с помощью OVITO, она
0009 казалось, что ориентация диполя и эллипсоида не
заморожена. Кажется, они вращаются (более или менее) свободно. Но расстояние
между диполем и эллипсоидом сохранилось. (Но я,
, определенно могу ошибаться при использовании OVITO.)
Признаюсь, отчасти я ответил, чтобы продвигать код MOLC.
(Это действительно круто.) Но если есть способ запустить эту симуляцию с
fix/rigid вместо этого, то это может быть лучше. MOLC пары_стили
и bond_styles трудно использовать без документации.
Андрей
P.S. Если кому-то интересно, я использую свою измененную, обновленную версию
его файла «in.ellipsoid», где я изменил команду дампа на
, включая информацию о диполях, чтобы упростить визуализацию.
Я
прикрепил этот входной скрипт к этому сообщению. Остальная часть файла
«in.ellipsoids» такая же, как и то, что он опубликовал. Я использую эти инструкции
для отображения направлений эллипсоидов и диполей в OVITO:
jewettai/moltemplate/blob/32ff0444a9e15c18746ac380d3ce04385aee2438/examples/coarse_grained/MOLC/ellipsoids/README_visualization_OVITO.txt
Можно визуализировать траекторию (файл дампа) программой OVITO (www.ovito.org). Однако вам придется определить несколько параметров. Вызовите ovito, используя: ovito traj.lampstrj На правой панели ovito, в разделе "Дамп LAMMPS" нажмите «Файл содержит временной ряд», чтобы отобразить всю траекторию. Затем нажмите кнопку «Редактировать сопоставление столбцов» и введите поля, как указано в файле "README_visualization_OVITO_settings.png", расположенном здесь: https://github.com/jewettaij/moltemplate/blob/master/examples/coarse_grained/MOLC/ Отелло М. Росциони [email protected]
(Вы должны изменить размер частиц по умолчанию и уменьшить длину диполя
, чтобы увидеть что-либо.
Также полезно, если вы отображаете только одну молекулу
вместо всей системы.)
in.ellipse (2,23 КБ)
Стив_Плимптон1
#5
Привет! Я пришел к этой теме с опозданием, но я думаю, что текущий Rix Rigid должен правильно работать с телами, состоящими из смеси точечных, сферических или эллипсоидных частиц,
любой из которых может иметь назначенный им точечный диполь. А точечный диполь должен вращаться вместе с телом. Если это не работает, вероятно, это ошибка.
Эндрю, самым простым тестом будет двухчастичный жесткий димер (точечные частицы) с диполем, назначенным одной или обеим точечным частицам.
Можете ли вы запустить этот тест с OVITO или выгрузить ориентацию тела и диполя, чтобы увидеть, остаются ли тела жесткими?
Только для простой системы с двумя корпусами.
Стив
jewettaij
#6
Привет! Я пришел к этой теме с опозданием, но я думаю, что текущий Rix Rigid должен правильно работать с телами, состоящими из смеси точечных, сферических или эллипсоидных частиц,
любому из которых может быть назначен точечный диполь. А точечный диполь должен вращаться вместе с телом. Если это не работает, вероятно, это ошибка.Эндрю, самым простым тестом будет двухчастичный жесткий димер (точечные частицы) с диполем, назначенным одной или обеим точечным частицам.
Можете ли вы запустить этот тест с OVITO или выгрузить ориентацию тела и диполя, чтобы увидеть, остаются ли тела жесткими?
Только для простой системы с двумя корпусами.
Привет, Стив, Аксель и Сумик
Кажется, я выяснил причину проблем Сумика с температурой, и это не то, что я думал.
Молекулы жесткие. Эллипсоид и диполь действительно сохраняют ту же ориентацию и положение, что и следовало ожидать от жесткой молекулы. (Это верно, когда я уменьшаю размер системы до одной жесткой молекулы или когда я моделирую исходную полноразмерную систему.)
Прошу прощения за ложную тревогу. (Когда я попытался просмотреть траекторию в OVITO, похоже, я неправильно угадал значения столбцов кватернионов. Это легко сделать. Кстати, исправленные настройки OVITO включены в изображение PNG, которое является частью вложения, прилагаемого к этому пост.)
Итак, почему такая странная температура? Согласно документации, для асферических частиц необходимо использовать «fix nvt/asphere» для корректного термостатирования эллипсоидальных частиц. Но я не могу придумать, как совместить этот интегратор с жесткой фиксацией. Возможно, это источник проблемы.
Я попытался смоделировать систему Сумика, используя несколько различных термостатов, в том числе фиксированный ланжевен, а также первоначальный выбор Сумика («жесткий ED fxrigid/nvt/small molecule temp 2,0 2,0 0,1»).
Когда я использовал его оригинальный термостат («fxrigid ED hard/nvt/small molecule temp 2.0 2.0 0.1»), системе потребовалось некоторое время для уравновешивания. Сообщается, что температура значительно выше заданной температуры (примерно 2,7 вместо 2,0). Но, возможно, я недостаточно долго ждал уравновешивания (всего 2000 временных шагов).
Если сомневаетесь, используйте самый простой термостат: почините ланжевен. Когда я использую fix langevin (вместе с «fxrigid all hard/nve/small molecule»), заявленная температура также была слишком высокой. (Опять же, примерно 2,8 вместо 2,0) (Я получаю аналогичное поведение, когда использую «зафиксировать твердую/малую молекулу ланжевена 2,0 2,0 0,5 123456»)
Однако, если я не ошибаюсь, использование «зафиксировать ланжевена» в конечном итоге должно привести к созданию системы с правильную кинетическую энергию после достижения теплового равновесия (даже если сообщаемая температура выше, чем должна быть, и вращательное движение недостаточно демпфировано).
Так что, вероятно, я бы поступил так, будь я на месте Сумик. (Это называется «Метод Ланжевена № 1» в прикрепленном файле «run.in».) Мне любопытно, есть ли у кого-нибудь идея получше.
Андрей
P.S. Если кому-то интересно, правильные настройки OVITO включены в конце этого письма в прикрепленном файле .gz. Упрощенный сценарий ввода «run.in» LAMMPS содержит настройки интегратора и термостата. Вы можете попробовать разные термостаты и посмотреть, что произойдет. (Вы можете изменить количество молекул в системе, отредактировав файл «system.lt» и следуя инструкциям в комментариях и файлах README.)
hard_ellipsoid_dipole_moltemplate.tar.gz (196 КБ)
Steve_Plimpton1
#7
Итак, почему такая странная температура? Согласно документации, для асферических частиц необходимо использовать «fix nvt/asphere» для корректного термостатирования эллипсоидальных частиц.
Но я не могу придумать, как совместить этот интегратор с жесткой фиксацией. Возможно, это источник проблемы.Для отдельных частиц фикс nvt/asphere хорош. Но для твердых тел fix hard/nvt/small должен делать то же самое. И есть вариант Ланжевена, чтобы использовать его в качестве термостата вместо NoseHoover. Это будет регулировать как поступательную, так и вращательную степень свободы набора тел.
Вы также должны быть осторожны при измерении температуры системы. Вы должны использовать вычисление temp/body.
Стив
аколмей
#8
andrew,
температура, сообщаемая в термальном выводе, по умолчанию получена из «вычисления температуры», но этот вычисление не знает о расширенных частицах.
так что вам нужно сделать:
вычислить ext все вычислить temp/asphere
thermo_modify temp ext
, чтобы получить правильную температуру, указанную в термовыходе.
При использовании любых жестких фиксаторов они автоматически вычисляют собственные внутренние температуры для перемещения и вращения, а также подсчитывают и сообщают об удаленных степенях свободы из-за протяженных частиц. При использовании «внешних» термостатов, таких как fix langevin, они будут учитывать только точечные частицы и использовать экземпляр вычисления температуры внутри, чтобы получить текущую температуру группы частиц, с которыми они работают.
еврейский
#9
Эндрю,
температура, сообщаемая в термальном выводе, по умолчанию получена из «вычисления температуры», но это вычисление не знает о расширенных частицах.
так что вы должны сделать:вычислить ext все вычислить temp/asphere
thermo_modify temp ext, чтобы получить правильную температуру, указанную в термовыходе.
Спасибо, Аксель. Что бы это ни стоило, я попытался поиграть с использованием «compute temp/asphere» и «compute_modify extra/dof», но я все еще получаю температуры, которые, как сообщается, (30%-50%) слишком высокие, что примерно похоже о чем сообщил Сумик.
(Предложение Стива использовать «вычислить температуру/тело» не работает, потому что «Вычисление температуры/тела требует тела в стиле атома». Что касается вашего предложения, я не могу использовать группу «все» с «вычислить температуру/асферу», потому что только половина частиц асферические. Вместо этого я попытался использовать для этого группу «сфероидов», в которой есть только асферические частицы. Но это означает, что в настоящее время я рассчитываю кинетическую энергию только сфероидов без учета кинетической энергии от точечных диполей, которые могут способствовать возникновению проблемы.)
Я сдаюсь. Я позволю Сумику продолжить, если ему понадобится дополнительная помощь.
На мой взгляд, это крайняя проблема, которая не затрагивает многих пользователей.
Но я сильно подозреваю, что система ведет себя правильно (уравновешивает правильную температуру), даже если температура сообщается неправильно.
Прилагается обновленная версия входного скрипта «run.in», которая включает в себя различные настройки, которые я пробовал. (Это часть прилагаемого архива .gz. Соответствующие строки из «run.in» 34-38,68) (Если бы у меня было больше времени поиграть с этим, я бы вычислил температуру по кинетической энергии, чтобы убедиться, что это правда, а также прочитал документацию и исходный код, чтобы глубже понять, что происходит.)
Эндрю
При использовании любых жестких исправлений они будут автоматически вычислять собственные внутренние температуры для перемещения и вращения, а также подсчитывать и сообщать об удаленных степенях свободы из-за протяженных частиц. При использовании «внешних» термостатов, таких как fix langevin, они будут учитывать только точечные частицы и использовать экземпляр вычисления температуры внутри, чтобы получить текущую температуру группы частиц, с которыми они работают.
П.С.
Спасибо. Это имеет смысл.
Я понимаю, что это помимо того, о чем вы здесь говорили, но или в записи, кажется, не имеет значения, использую ли я:
- «fix hard/nvt/small»
- «фиксация жесткого/низкомолекулярного ланжевена»
- «фиксация ланжевена» + «фиксация жесткая/малая/nve»
…Во всех случаях указанная температура слишком высока (между 30% и 50%).
(См. строки 52, 63-64, 68 «run.in» в прикрепленном файле .gz.)
Если температура просто сообщается неправильно, то имеет смысл, что не имеет значения, как я интегрирую уравнения движения. Кстати, прикрепленный файл .gz содержит изображение того, как выглядит каждая молекула.
hard_ellipsoid_dipole_moltemplate_2021-5-01.tar.gz (196 КБ)
пользователи-лампы
#10
Спасибо всем за ваши чрезвычайно полезные предложения.
Особенно Андрей. Я успешно это реализовал.
С уважением,
Soumik
Геоид, эллипсоид, сфероид и датум и их взаимосвязь — ArcMap
Геоид определяется как поверхность гравитационного поля Земли, которая примерно равна среднему уровень моря. Он перпендикулярен направлению гравитационного притяжения. Так как масса земли не во всех точках однородна, а направление силы тяжести меняется, форма геоида неправильная.
Нажмите на ссылку ниже, чтобы получить доступ к веб-сайту, поддерживаемому Национальным управлением океанографии и атмосферы (NOAA). На веб-сайте есть ссылки на изображения, показывающие интерпретации геоида под Северной Америкой: https://www.ngs.noaa.gov/GEOID/.
Для упрощения модели были разработаны различные сфероиды или эллипсоиды. Эти термины используются взаимозаменяемо. В оставшейся части этой статьи будет использоваться термин сфероид.
Сфероид — это трехмерная фигура, созданная из двумерного эллипса. Эллипс представляет собой овал с большой осью (более длинная ось) и малой осью (более короткая ось).
Если вы повернете эллипс, форма повернутой фигуры будет сфероидом.
Большая полуось составляет половину длины большой оси. Малая полуось составляет половину длины малой оси.
Для Земли большая полуось — это радиус от центра Земли до экватора, а малая полуось — это радиус от центра Земли до полюса.
Один конкретный сфероид отличается от другого длинами большой и малой полуосей. Например, сравните сфероид Clarke 1866 с GRS 1980 и WGS 19.84 сфероида, основанные на измерениях (в метрах) ниже.
| Spheroid | Semimajor axis (m) | Semiminor axis (m) |
|---|---|---|
Clarke 1866 | 6378206.4 | 6356583.8 |
GRS80 1980 | 6378137 | 6356752. |
WGS84 1984 | 6378137 | 6356752.31424518 |
31414A particular spheroid can be selected for use in a specific geographic area, because that particular spheroid does an exceptionally good job of mimicking the geoid for that часть мира. Для Северной Америки предпочтительным сфероидом является GRS 1980, на котором основаны North American Datum 1983 (NAD83).
База данных строится поверх выбранного сфероида и может включать локальные изменения высоты. Со сфероидом вращение эллипса создает абсолютно гладкую поверхность по всему миру. Поскольку это не очень хорошо отражает реальность, локальный датум может включать локальные вариации высот.
Базовый датум и сфероид, на который ссылаются координаты набора данных, могут изменить значения координат.
Ниже приводится наглядный пример с использованием города Беллингем, штат Вашингтон. Сравните координаты Беллингема в десятичных градусах, используя NAD27, NAD83 и WGS84. Очевидно, что в то время как NAD83 и WGS84 выражают почти идентичные координаты, NAD27 сильно отличается, потому что основная форма Земли выражается по-разному с помощью используемых датумов и сфероидов.
| Datum | Longitude | Latitude | |||
|---|---|---|---|---|---|
NAD 1927 | -122.466
|
