Википедия эллипс: HTTP 429 — too many requests, слишком много запросов

wpf — Реакция на клик по нескольким элементам управления одновременно

Нормальное поведение практически любых GUI на клик мышью по одному из контроллов — вызвать Event для этого контролла. Если же в одном месте находится несколько элементов управления, событие вызывается только для «верхнего».

Подскажите, пожалуйста, возможно ли узнать обо всех таких «попаданиях»? В моём случае есть Canvas с кучей дочерних Ellipse’ов, которые и должны реагировать на клик.

ЗЫ: Не вижу особых проблем для того, чтобы посчитать пересечения вручную, но хотелось бы обойтись без костылей 🙂

• wpf
• .net
• события

Пишите свой детектор столкновения курсора с объектами, это просто. wiki/Эллипс в помощь.

 System.Windows.Forms.Cursor.Position

Используйте этот объект для получения координат мыши. Может еще потребоваться линейная конверсия координат из системы координат в которой задан эллипс в систему координат в которой задан курсор или обратно.

2

Поскольку у вас в тегах есть WPF, почитайте про Routed Events, и про их типы — восходящие и нисходящие. Это то, что вам нужно.

WPF генерирует щелчок всегда только для лежащего сверху элемента — это не лечится. Но свою проблему вы можете решить так: завести список, в которому будут храниться все эллипсы, над которыми сейчас мышь. В обработчике события MouseEnter эллипса добавлять его в список, а в MouseLeave — удалять. Это всего две строчки. А в клике по любому эллипсу без плясок с координатами используйте этот список.

Нашел вот такую штуку (VisualTreeHelper.HitTest), результаты положительные. Нашел, к сожалению, самостоятельно, но всё равно ОГРОМНОЕ всем спасибо за внимание и советы!

Hit Testing in the Visual Layer.

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Сверление квадратных отверстий / Этюды // Математические этюды

Сверление квадратных отверстий / Этюды // Математические этюды

Математические этюды

К списку

В фильме ⁠⁠«Круг­лый тре­уголь­ник Рело» рас­ска­зы­ва­ется о фигу­рах, обла­дающих посто­ян­ной шири­ной.

\circ$ отно­си­тельно сто­рон квад­рата и равны $k\cdot(\sqrt{3}+1)/2$ и $k\cdot(1/\sqrt{3}-1)/2.$

Площадь неза­ме­тён­ных уго­лоч­ков состав­ляет всего около $2\%$ от площади всего квад­рата!

Теперь, если сде­лать сверло в виде тре­уголь­ника Рело, то можно будет свер­лить квад­рат­ные отвер­стия с немного скруг­лен­ными угол­ками, но абсо­лютно прямыми сто­ро­нами!

Оста­лось сде­лать такое сверло… Вер­нее, само-то сверло сде­лать несложно, нужно только чтобы оно напоми­нало в сече­нии тре­уголь­ник Рело, а режущие кромки совпа­дали с его верши­нами.

Труд­ность заклю­ча­ется в том, что, как уже было отме­чено выше, тра­ек­то­рия цен­тра сверла должна состо­ять из четырёх дуг эллип­сов. Визу­ально эта кри­вая очень похожа на окруж­ность и даже матема­ти­че­ски близка к ней, но всё же это не есть окруж­ность. А все экс­цен­трики (круг, поса­жен­ный на круг другого ради­уса со смещён­ным цен­тром), исполь­зу­емые в тех­нике, дают движе­ние строго по окруж­но­сти.

В 1914 году английский инже­нер Гарри Джеймс Уаттс при­думы­вает, как устро­ить такое свер­ле­ние. На поверх­ность он накла­ды­вает направ­ляющий шаб­лон с про­ре­зью в виде квад­рата, в кото­ром ходит сверло, встав­лен­ное в патрон со «сво­бодно пла­вающим в нём свер­лом». Патент на такой патрон был выдан фирме, начавший изго­тов­ле­ние свёрл Уаттса в 1916 году.

Мы же восполь­зу­емся дру­гой извест­ной кон­струкцией. При­крепим сверло жёстко к тре­уголь­нику Рело, помещён­ному в квад­рат­ную направ­ляющую рамку. Сама рамка фик­си­ру­ется на дрели. Оста­лось теперь пере­дать враще­ние патрона дрели тре­уголь­нику Рело.

Помогает решить эту тех­ни­че­скую про­блему кон­струкция, кото­рую вы навер­няка много раз видели под днищем про­езжавших по улице гру­зо­вых автомо­би­лей — кар­дан­ный вал. Эта пере­дача полу­чила своё назва­ние в честь Дже­ро­ламо Кар­дано.

Дже­ро­ламо КАР­ДАНО 1501—1576

Когда в 1541 году импе­ра­тор Карл V три­умфально вошёл в заво­ё­ван­ный Милан, рек­тор кол­легии вра­чей Кар­дано шёл рядом с бал­да­хи­ном. В ответ на ока­зан­ную честь он пред­ложил снаб­дить коро­лев­ский экипаж под­вес­кой из двух валов, каче­ние кото­рых не выве­дет карету из гори­зон­таль­ного положе­ния […]. Спра­вед­ли­вость тре­бует отме­тить, что идея такой системы вос­хо­дит к антич­но­сти и что по край­ней мере в «Атлан­ти­че­ском кодексе» Лео­нардо да Винчи име­ется рису­нок судо­вого компаса с кар­дан­ным под­ве­сом. Такие компасы полу­чили рас­про­стра­не­ние в пер­вой поло­вине XVI века, по-видимому, без вли­я­ния Кар­дано.

Гин­ди­кин С. Г. Рас­сказы о физи­ках и матема­ти­ках.

Теперь у нас всё готово к свер­ле­нию. Возьмём фанер­ный лист и… высвер­лим квад­рат­ное отвер­стие! Как уже гово­ри­лось, сто­роны будут строго прямыми и лишь уголки немного скруг­лены. При необ­хо­димо­сти их можно подпра­вить надфи­лем.

Лите­ра­тура

Weisstein E. Reuleaux Triangle.

Гин­ди­кин С. Г. Рас­сказы о физи­ках и матема­ти­ках.  — М. : МЦНМО, 2006.

Фигуры посто­ян­ной ширины // Матема­ти­че­ская состав­ляющая / Ред.-сост. Н. Н. Андреев, С. П. Коно­ва­лов, Н. М. Паню­нин. — Вто­рое изда­ние, расши­рен­ное и допол­нен­ное. — М. : Матема­ти­че­ские этюды, 2019. — С. 84—85, 319—320.

Другие этюды раздела «Кривые (фигуры) постоянной ширины»

  Круглый треугольник Рело  Изобретая колесо

Математические этюды

{2}}}} — длина окружности вписанного ромба с вершинами на концах главной и второстепенной осей. Согласно книге Роберта Брингхерста «Элементы типографского стиля», детали эллипсов предложений зависят от характера и размера набора шрифтов и предпочтений типографа. Брингхерст пишет, что полное расстояние между каждой точкой — это «еще одна викторианская эксцентричность». В большинстве случаев чикагский эллипс слишком широк», — он рекомендует использовать ровные точки (с нормальным расстоянием между словами до и после) или тонкие точки (до одной пятой em) или предопределенный эллиптический знак U+2026.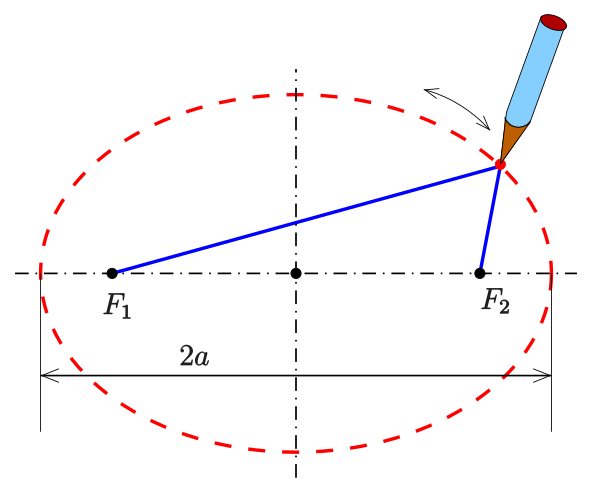

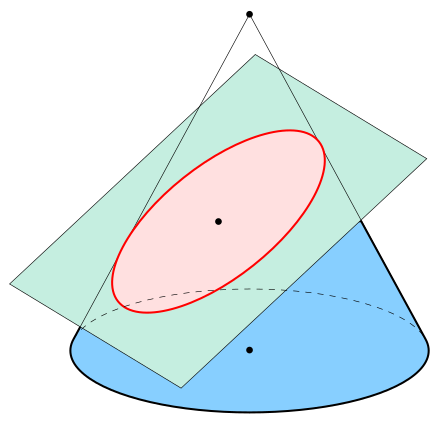{2}(x)}},dx}. Также легко строго доказать формулу поверхности, используя интегрирование следующим образом. 9{2}}}.} Для x ∈ [−a, a] {displaystyle xin [-a,a],} эта кривая является верхней половиной эллипса. Таким образом, двойной интеграл от y ( x ) {displaystyle y(x)} на интервале [ − a , a ] {displaystyle [-a,a]} является площадью эллипса: уравнение эллипса с центром в начале координат (0,0)(0,0)(0,0), задается эллипсом с центром в начале координат, то используются два вектора. Вариант метода бумажной полоски 1 используется наблюдение, что центр N { displaystyle N} бумажной полосы перемещается. на окружности с центром M {displaystyle M} (эллипс) и радиусом a + b 2 {displaystyle {tfrac {a+b}{2}}}. Таким образом, бумажную полоску в точке N {displaystyle N} можно разрезать на две половины, которые снова соединяются соединением с N {displaystyle N}, а скользящий конец K {displaystyle K} фиксируется посередине M {displaystyle M} (см. схему). После этой операции движение неизменной половины бумажной полоски остается неизменным. [12] Для этого варианта требуется только один скользящий башмак. Для f → 0 = ( 0 0 ), f → 1 = a ( cos θ sin θ ), f → 2 = b ( − sin θ cos θ ) { displaystyle {vec {f}} _ {0} = {0 выберите 0},;{ vec {f}}_{1}=a{потому что тета тета выбирает тета },; {vec {f}}_{2}=b{-sin theta Choose ;cos theta }} Вы получаете параметрическое представление стандартного эллипса {displaystyle theta}, повернутого вокруг угла Θ: две некруглые шестерни с одинаковым эллиптическим контуром, каждое панорамирование вокруг фокуса и расположение под прямым углом, плавное вращение и постоянный контакт. В качестве альтернативы они могут быть соединены звеньевой цепью или зубчатым ремнем, или, в случае велосипеда, основное кольцо может быть эллиптическим или иметь яйцевидную полость, похожую на форму эллипса. Такие эллиптические зубчатые колеса можно использовать в механических устройствах для создания переменной угловой скорости или крутящего момента за счет постоянного вращения оси привода или, в случае велосипеда, для обеспечения переменной скорости кривошипа с переменным механическим преимуществом при движении назад. {2}}}=0} , то точки находятся на двух сопряженных диаметрах (см. ниже). (Если a = b {displaystyle a=b}, эллипс представляет собой круг, а «сопряженный» означает «ортогональный».) Лучи одного фокуса отражаются от эллипса во втором фокусе. Это свойство имеет оптические и акустические приложения, напоминающие отражательную способность параболы (см. галерею Whisper). С математической точки зрения эллипс действительно является эллипсом. Его размеры составляют 1058 футов (322 м) по главной оси (восток-запад) и 903 фута (275 м) для его вторичной оси (север-юг). Его эксцентриситет рассчитывается как e = 0,52, а его фокусные точки находятся на расстоянии 552 футов (168 м) друг от друга, каждые 276 футов (84 м) от центра эллипса (восток и запад).

[1] В статистике двумерный случайный вектор ( X , Y ) {displaystyle (X,Y)} совместно эллиптически распределен, если его контуры изоплотности — места равных значений функции плотности — являются эллипсами. Концепция распространяется на любое количество элементов в случайном векторе, причем контуры изоплотности обычно представляют собой эллипсоиды.

Особым случаем является многомерное нормальное распределение. Эллиптические распределения важны в финансах, потому что, когда доходность активов распределяется вместе эллиптически, все портфели могут быть полностью охарактеризованы их средним значением и дисперсией, то есть два портфеля с одинаковым средним значением портфеля и дисперсией доходности портфеля имеют идентичные распределения доходности портфеля. [25] [26] Иногда бывает полезно найти эллипс минимального предела по ряду точек. Метод эллипсоидов очень полезен при решении этой задачи. Эллипс [1] — это форма, напоминающая овал или приплюснутый круг. В японских медиатекстах, таких как манга или видеоигры, многоточие встречается гораздо чаще, чем в английском, и в переводе часто заменяется другим знаком препинания.

Сам эллипс представляет собой отсутствие речи или «многозначительную паузу». В зависимости от контекста это может варьироваться от признания вины до выражения недоумения по поводу слов или действий другого человека.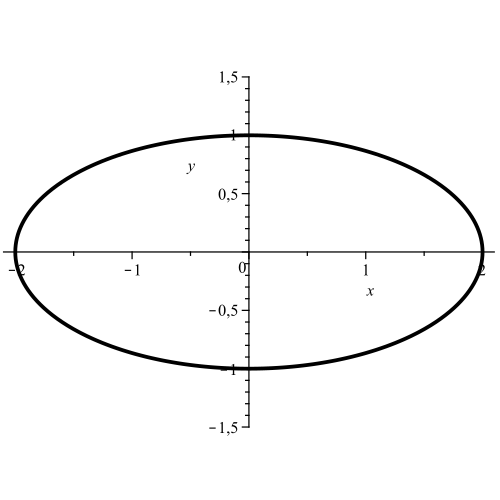 {2}}}=1} получается: Точки Для любого числа n фокальных точек n-эллипс представляет собой замкнутую и выпуклую кривую. [2] : (стр. 90) Кривая гладкая, если только она не проходит через камин. [5]: стр.7 В электронике относительную фазу двух синусоидальных сигналов можно сравнить, подав их на вертикальный и горизонтальный входы осциллографа.

Передняя публикация

Оборудование для очистки от загрязнений

11 октября 2022 г.

Siguiente Publicación

определение

11 октября 2022 г.

Кливленд-Клиффс Инк. (CLF)

Cleveland-Cliffs — крупнейшая компания по производству плоского стального проката в Северной Америке

15 мая 2023 г., 00:00 по восточноевропейскому времени

Генеральный директор Cleveland-Cliffs Лоуренко Гонсалвес избран председателем Американского института черной металлургии

Посмотреть новость Статья

15 мая 2023 г. , 00:00 по восточноевропейскому времени

Cleveland-Cliffs 2023 Годовое собрание акционеров

Посмотреть новость Статья

Посмотреть все новости

Cleveland-Cliffs Презентация для инвесторов

Cleveland-Cliffs выпустила свою последнюю презентацию для инвесторов. В этой презентации рассказывается о превращении Cleveland-Cliffs в крупнейшего производителя плоского проката и крупнейшего поставщика автомобильной стали в Северной Америке. Он охватывает операционную деятельность компании, ее дифференцированную, полностью интегрированную бизнес-модель и ее приверженность политике ESG, включая активное сокращение выбросов парниковых газов.

Посмотреть презентацию для инвесторов

Представляем неориентированные электротехнические стали MOTOR-MAX™

Cleveland-Cliffs Высокочастотные неориентированные электротехнические стали MOTOR-MAX (HF NOES) предлагают различные марки стали, специально разработанные для высокочастотных двигателей и генераторов.