Каноническое уравнение эллипса. Как построить эллипс?
Во-первых, правописание…. Пожалуйста, не повторяйте ошибок некоторых юзеров, которые запрашивают «элипс», «эллибз» и даже «элебс» 🙂 Эллипс.
Каноническое уравнение эллипса имеет вид , где – положительные действительные числа, причём . Определение эллипса я сформулирую чуть позже, а пока самое время отдохнуть от говорильни и решить распространённую
задачу:
Как построить эллипс?
Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:
Задача 96
Построить эллипс, заданный уравнением
Решение: сначала приведём уравнение к каноническому виду:
Зачем приводить? Большое преимущество канонического уравнения заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках .
В нашем случае :
Число называют большой полуосью эллипса;
число – малой полуосью;
отрезок называют большой осью эллипса;
отрезок – малой осью.
Очевидно, что значения «а» и «бэ» (в нашем примере , ) вместе центром симметрии (в нашем примере ) однозначно определяют эллипс.
Всё выглядит красиво, ладно, но есть один нюанс: я выполнил чертёж с помощью Приложения Геометрический Калькулятор. И вы тоже можете так поступить. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хоровод мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас (правда, поменьше). Поэтому для ручного построения чертежа крайне желательно найти дополнительные точки.
Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине
замороченного алгоритма и существенной загроможденности чертежа. В случае крайней необходимости обратитесь к учебнику, а в реальности же гораздо
удобнее воспользоваться средствами алгебры. Из уравнения эллипса на
черновике быстренько выражаем:
Построение с помощью циркуля и линейки мне не нравится по причине
замороченного алгоритма и существенной загроможденности чертежа. В случае крайней необходимости обратитесь к учебнику, а в реальности же гораздо
удобнее воспользоваться средствами алгебры. Из уравнения эллипса на
черновике быстренько выражаем:
Далее уравнение распадается на две функции:
– определяет верхнюю дугу эллипса;
– определяет нижнюю дугу эллипса.
Каноничный эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично! – ибо работы
будет в 4 раза меньше. Рассмотрим 1-ю координатную четверть, соответствующую функцию , и здесь напрашивается найти точки с абсциссами :
Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу же выяснится в ходе построения.
Отметим на чертеже точки (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию:
Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу.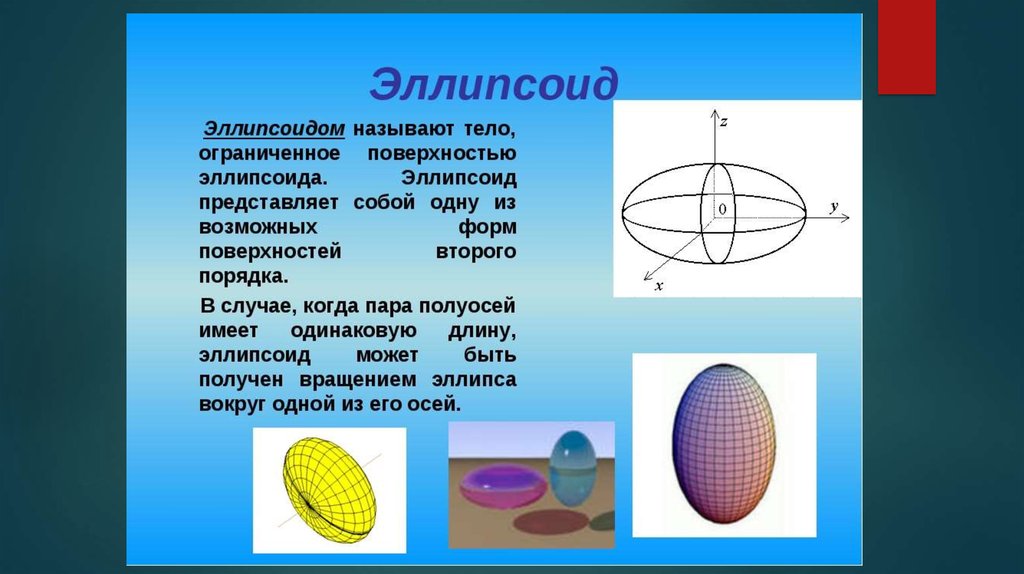
В результате должен получиться вполне симпатичный эллипс.
Кстати, не желаете ли узнать, что это за кривая?
3.3.2. Определение эллипса. Фокусы эллипса
3.2. Классификация линий второго порядка
| Оглавление |
Автор: Aлeксaндр Eмeлин
Урок 3. Окружность в перспективе. Как нарисовать кружку и вазу
В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк.
Содержание:
- Принципы рисования эллипсов
- Рисуем эллипсы
- Рисуем кружку
- Рисуем вазу
- Тест на рисование эллипсов
Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).
То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.
Принципы рисования эллипсов:
Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.
Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).
Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).
В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).
Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.
Рисуем эллипсы
Шаг 1. Для начала проведем две перпендикулярных оси.
Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.
А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.
Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.
Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.
Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.
Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее.
Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.
Рисуем кружку
Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.
Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.
Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.
Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.
Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.
Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза.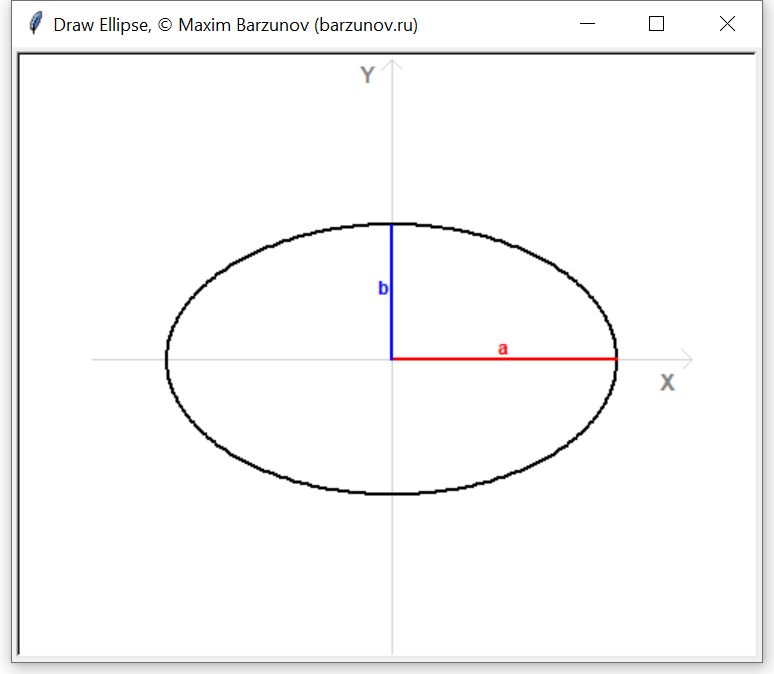 Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.
Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.
Шаг 5. Найдем расположение ручки и ее общие пропорции, а затем схематично наметим основные отрезки, формирующие ее контур. Их наклоны определяем методом визирования (а где-то — на глаз).
Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!
Рисуем вазу
В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.
В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму.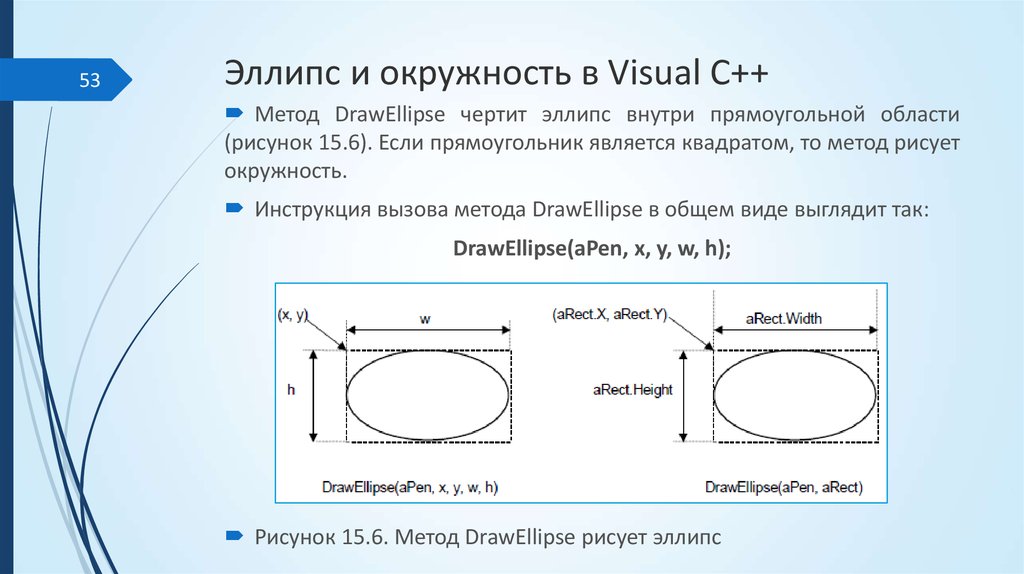 Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).
Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).
Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.
Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.
Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).
Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).
Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.
Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.
Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины.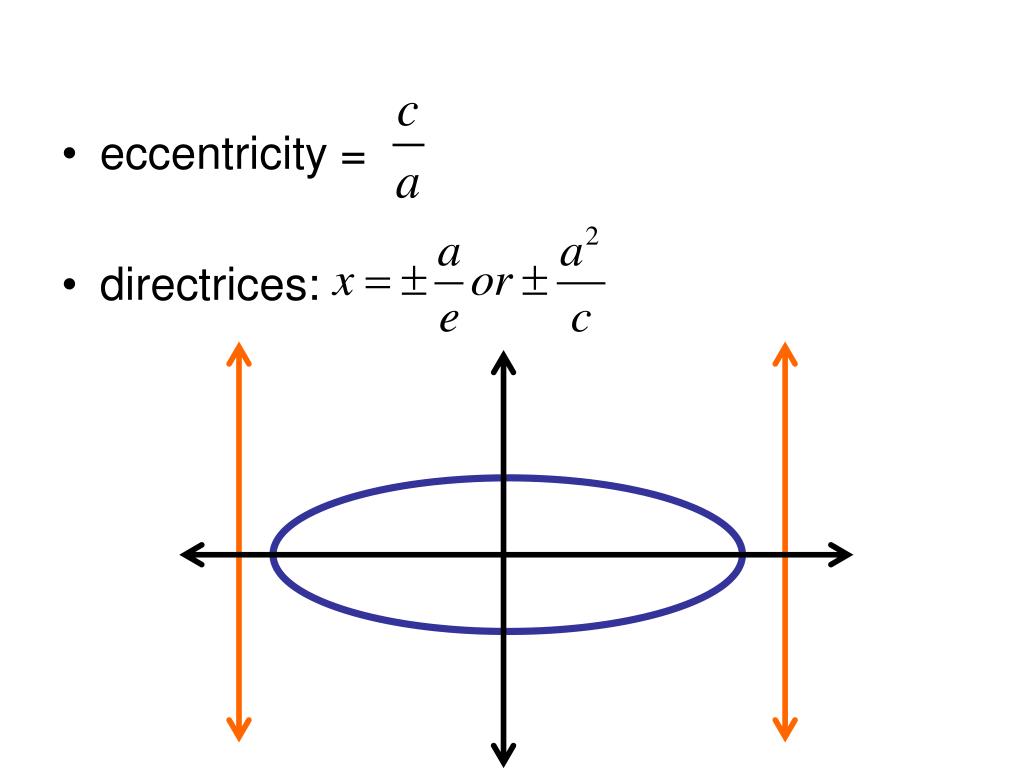 Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!
Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Cтатистика На весь экран
Юлия Отрубянникова
← 2 Линейная перспектива4 Светотень →
Как использовать многоточие в английском языке
Что такое многоточие? Да ладно…
Многоточие — это последовательность из трех точек, используемых в качестве знака препинания, как и выше. Множественное число эллипсиса — эллипсы. Слово эллипсис происходит от греческого слова, которое означает упущение или опущение. Мы используем многоточие, чтобы исключить слова из предложения или показать незаконченные предложения или мысли. Давайте подробнее рассмотрим, как мы используем их в английском языке .
Множественное число эллипсиса — эллипсы. Слово эллипсис происходит от греческого слова, которое означает упущение или опущение. Мы используем многоточие, чтобы исключить слова из предложения или показать незаконченные предложения или мысли. Давайте подробнее рассмотрим, как мы используем их в английском языке .
Как выглядит многоточие?
Как я уже сказал, многоточие — это последовательность из трех точек. Оно может стоять в начале, в середине или в конце предложения. Если он стоит в конце предложения, после него обычно нужно ставить знак препинания, особенно в официальном письме.
Подожди, где ты…?
Они сказали, что будут… .
Оставляете ли вы пробелы вокруг точек или между ними, зависит от того, какой стиль вы используете. Оксфордское руководство по стилю говорит, что вы должны оставлять пробел до и после точек, но не между ними. Это стиль, который мы используем здесь. Однако в других руководствах по стилю говорится, что между точками должны быть пробелы, например: . . . . Какой бы стиль вы ни выбрали, оставайтесь последовательными.
. . . Какой бы стиль вы ни выбрали, оставайтесь последовательными.
Грамматика для собеседований на английском языке
Как использовать многоточие в предложении
Мы можем использовать многоточие, чтобы показать, что мы намеренно пропустили часть предложения, цитаты или фразы. Мы делаем это, когда нам нужно опустить менее релевантную информацию, чтобы сделать предложение более читабельным или более понятным. Эллипсы помогают нам экономить место в письме.
Не пытайтесь дозвониться до меня. Меня не будет с 9 утра до 9 вечера, так что весь день.
Не пытайтесь дозвониться до меня. Меня не будет… весь день.
Я пошел на работу в понедельник утром, это был прекрасный солнечный день, и я встретил Джона, бегущего по коридору.
Я пошел на работу в понедельник утром… и встретил Джона, бегущего по коридору.
Если вы хотите пропустить начало предложения, многие писатели используют многоточие плюс заглавную букву в квадратных скобках:
… [Я]был прекрасный солнечный день, и я встретил Джона, бегущего по коридору.
Другие авторы не считают многоточие здесь необходимым. Вы можете выбрать стиль, который предпочитаете, но не меняйте свое мнение на полпути к написанию!
Многоточие часто используется в более формальном письме, особенно в академическом письме, когда вы цитируете что-то или кого-то еще. Вот цитата Джейн Остин, английской писательницы, чтобы показать, как мы можем это сделать:
«Человек, будь то джентльмен или леди, который не получает удовольствия от хорошего романа, должен быть невыносимо глуп».
Мы можем сократить его так:
«Человек… который не получает удовольствия от хорошего романа, должен быть невыносимо глуп».
7 самых сложных языков для изучения (особенно если вы говорите по-английски!)
Использование многоточия для обозначения паузы
Мы также можем использовать многоточие для обозначения паузы или нерешительности в речи или мысли. Таким образом мы используем многоточие, когда сообщаем, что кто-то сказал или подумал. Точно так же мы можем использовать многоточие, чтобы показать напряжение или изменение настроения. Обычно мы используем это в неформальной письменной форме; не в формальном или академическом письме.
Точно так же мы можем использовать многоточие, чтобы показать напряжение или изменение настроения. Обычно мы используем это в неформальной письменной форме; не в формальном или академическом письме.
Давайте рассмотрим несколько примеров:
«Посмотрим… где мы были?»
«Хм, я не уверен…»
Бен услышал шум в коридоре снаружи. Но он был в здании один…
Как видите, в этих неформальных предложениях, если многоточие стоит в конце фразы или предложения, нам не нужно ставить точку.
Самые распространенные слова английского языка
Чрезмерное использование многоточия
Многоточие полезно при письме. Но иногда у нас может быть слишком много хорошего. В последние годы люди все чаще используют многоточие.
Они могут использовать его для замены другого знака препинания:
Как идет игра…
В правильном письменном языке это должен быть вопросительный знак, а не многоточие.
Люди также используют его, чтобы показать место, где мы говорим гм или гм , если мы говорим. Вы можете получать электронные письма следующего вида:
Я еще ничего не слышал от отдела продаж… есть еще кто-нибудь, с кем я могу поговорить? Не знаю, что делать… жду вашего ответа.
В этих предложениях не должно быть многоточия. Электронное письмо было бы намного понятнее и выглядело бы более профессионально, если бы оно было написано так:
Я еще ничего не слышал о продажах. Есть еще кто-нибудь, с кем я могу поговорить? Не уверен, что делать; Я жду Вашего ответа.
Так что используйте многоточие с осторожностью!
Ellipses
Круги и эллипсы
. эллипсы и круги. Студенты должны быть дали следующее определение, а затем предложили изучить модель ВСП представляющее геометрическое определение.
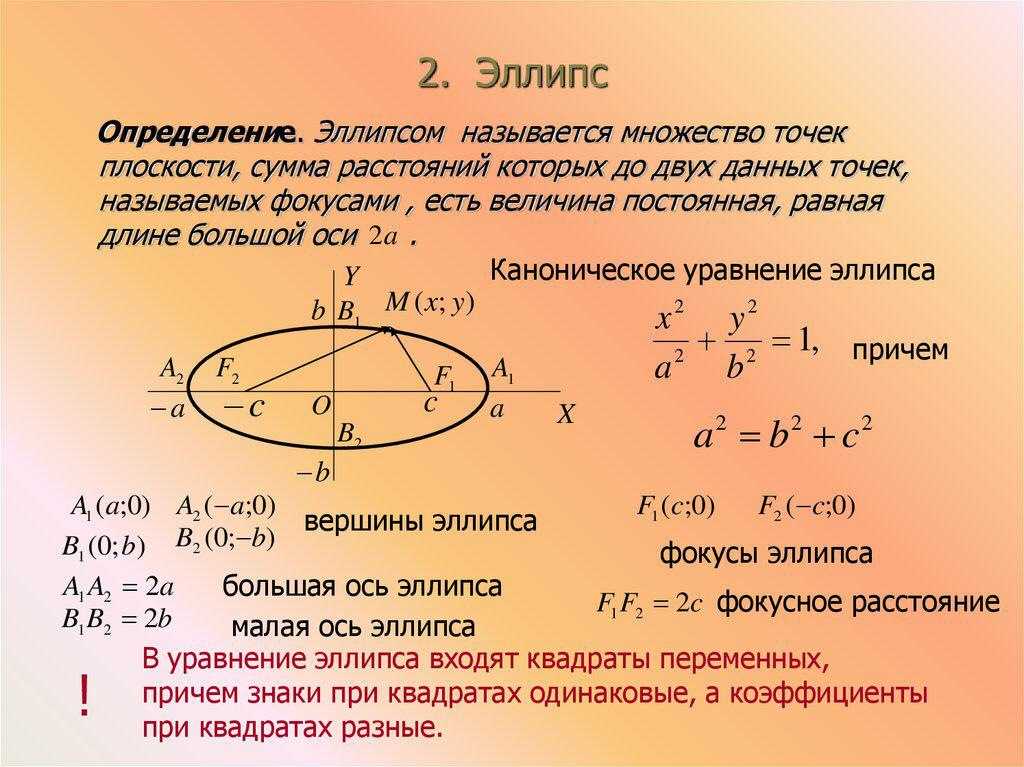
Определение: Эллипс – это множество точек, такое что сумма расстояний от каждой точки до двух фиксированных точек (фокусов) постоянно. |
Пожалуйста см. прикрепленный файл GSP для демонстрации определения
Учащиеся могут заметить изменения, происходящие в эллипсе, фокусы перемещаются. Что это форма выглядит, когда фокусы сдвинуты дальше друг от друга? Как выглядит форма, когда очаги находятся близко друг к другу? Какую форму ты имеют, когда фокусы находятся друг над другом? Цель исследования — помочь учащимся осознать, что два вырожденных случая эллипса: окружность и прямая.
Нажмите здесь, чтобы поэкспериментировать с различным расположением фокусов.
С помощью прямого обучения объясните учащимся, что каждый
эллипс имеет два важных отрезка.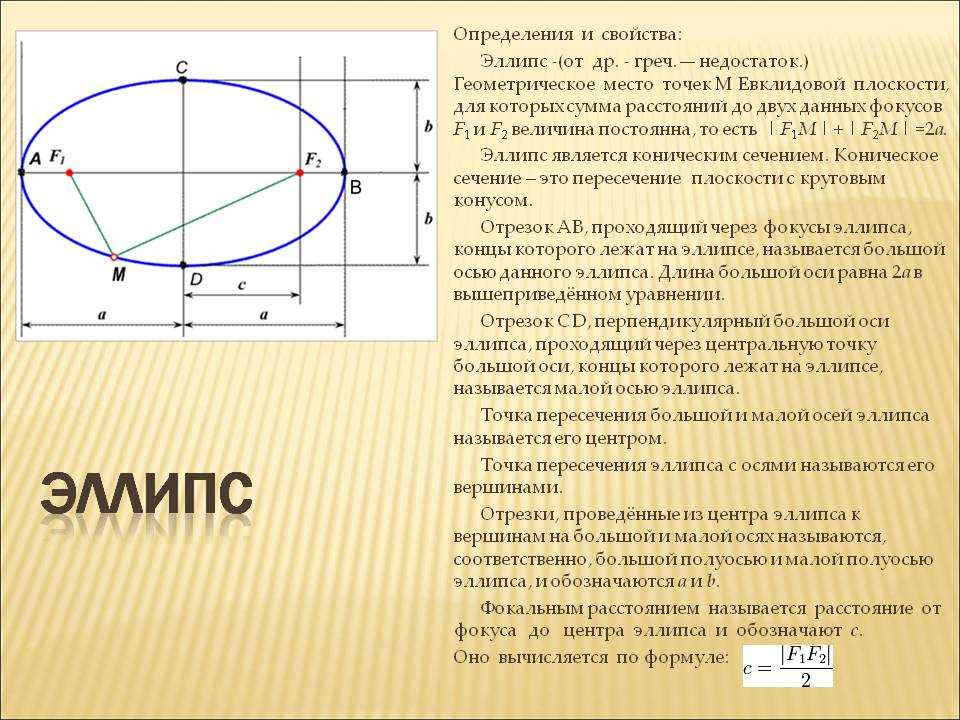 Одна из них называется большой осью, отрезок линии BC показан ниже, а
другая называется малой осью, отрезок DE. Эти оси представляют собой два сегмента
симметрия.
Одна из них называется большой осью, отрезок линии BC показан ниже, а
другая называется малой осью, отрезок DE. Эти оси представляют собой два сегмента
симметрия.
Следующие вопросы, полученные от
a. с помощью линейки и калькулятора
b. только с компасом
Вопросы
- Использование прикрепленный файл GSP, который дает измерение большой оси BC , определить длину F1P + F2P без проведение дополнительных измерений. Объясни свои рассуждения.
Подсказка: Поместите точку P на точку E для установления любых отношений.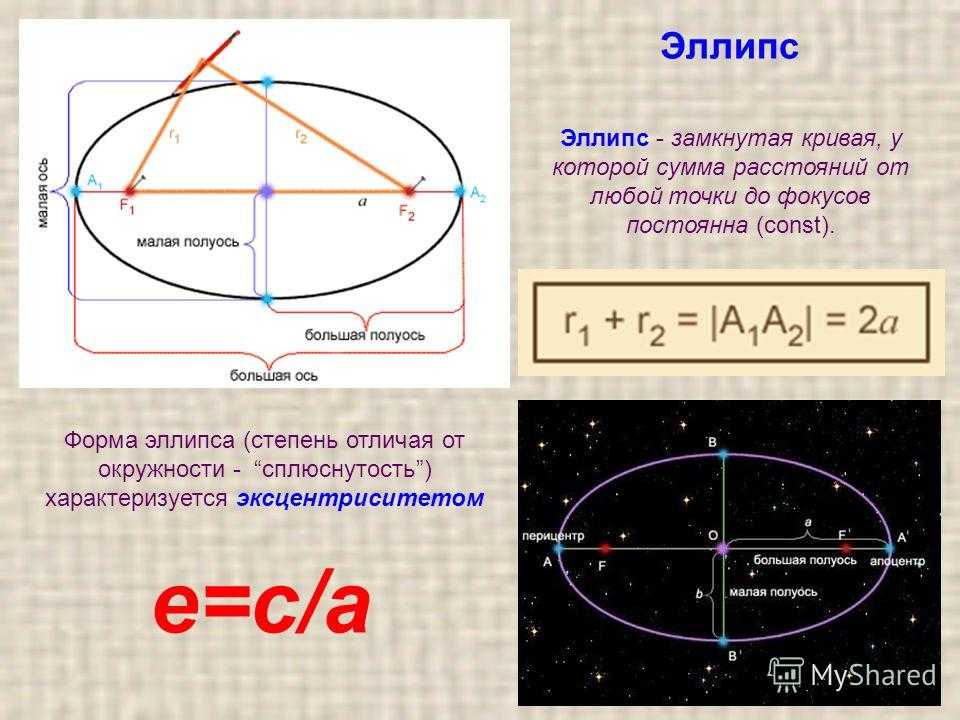 Также поместите точку P на точку C. Что вы заметили?
Также поместите точку P на точку C. Что вы заметили?
- Использование файл GSP из задачи номер один, обратите внимание на точку E лежит на одном конце малой оси эллипса и указывает F1 и F2 — фокусные точки эллипсов. Длина большой оси БК 11,39 см. Без измерения определить длины EF1 и EF2 . Объясните свои рассуждения.
- Использование прикрепленный файл GSP, ваш ответ от предыдущий вопрос вместе с тем, что длина малой оси (сегмент ED ) равна 8,54 для определения длин сегментов ОФ1 и OF2 .
- На основе на ваши ответы на предыдущие вопросы, какая связь между OC , OE и OF2?
- Используйте
заданные измерения для расчета фокусных точек эллипса
ниже.
 Объясните свой метод.
Объясните свой метод.
- Объяснить как бы вы нашли фокусные точки, используя только компас.
Чтобы получить ответы на эти вопросы, щелкните здесь
свойств, их следует ввести в стандартное уравнение эллипс. Учащимся следует дать следующую информацию, 92 позиции меняются местами при растяжении эллипса в направлении Y. Расстояние от центр каждой вершины равен a единиц и расстояние от центра до концов малой оси составляет б ед. Вспомним из предыдущего упражнения, что эллипсов два фокуса расположены на расстоянии c единиц от центра на большой оси и находятся по соотношению 92 . Ширину эллипсов находят, находя широкая прямая кишка, которая находится на заданном расстоянии выше и ниже каждого фокуса определяется значением
.
Вспоминая, что окружность является вырожденным случаем эллипса, студенты должны иметь следующее.
Круг это набор всех точек плоскости, равноудаленных от фиксированной точки, называемой центр. Фиксированное расстояние – это радиус. Стандартная форма круга центр которого находится в точке
.
Радиус r единиц. |
Учащиеся должны использовать Графический калькулятор для
значения для (h,k) и a и b для эллипса. С каждым другим эллипсом они создают они
следует регистрировать расположение очагов и длину широкой прямой кишки.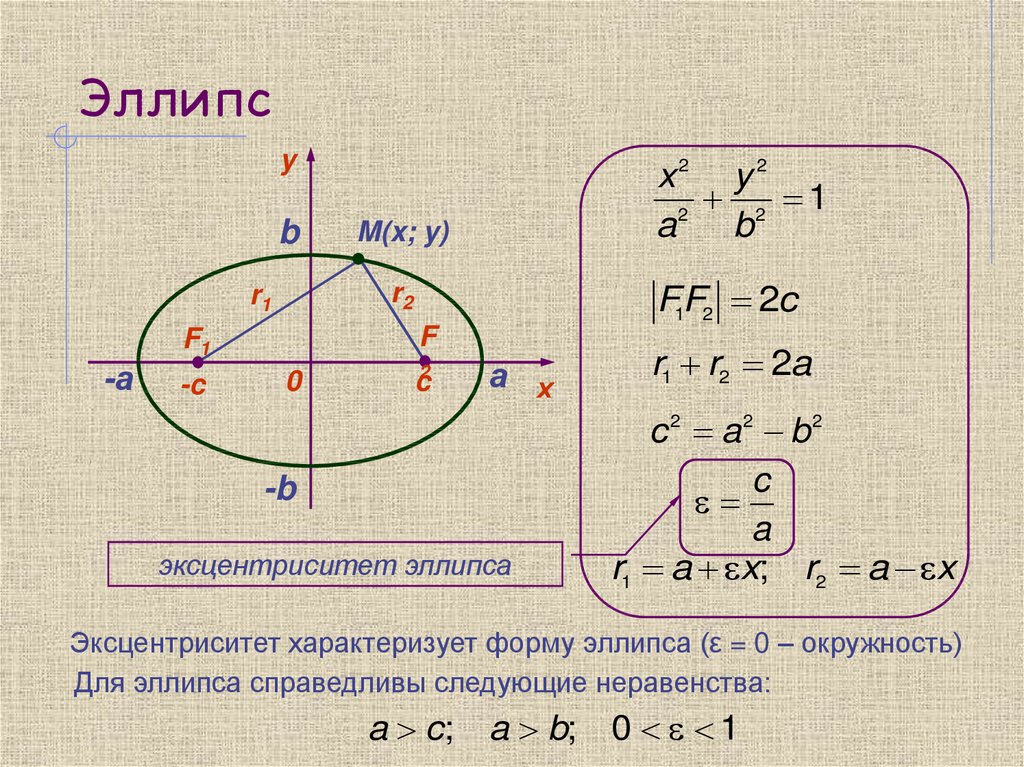
 Объясните свой метод.
Объясните свой метод.