Как научить ребенка считать в уме: быстрый и проверенный способ
Несмотря на то, что в школе не требуют, чтобы к первому классу ребенок освоил навык устного счета, часть родителей стремится начать обучение как можно раньше. В каком возрасте ребенок должен считать в уме, с чего начинать обучение и какие методы обучения выбрать, «Газете.Ru» рассказали преподаватель математики и специалист по ментальной арифметике.
Умение хорошо и быстро считать не влияет напрямую ни на умственные способности, ни на способность к обучению школьным дисциплинам, объяснил преподаватель по математике и анализу данных Школы программистов МШП Дмитрий Коняев. Тем не менее, по мнению эксперта, такой навык крайне полезен и сильно облегчает жизнь, так что не будет лишним приобрести его уже в дошкольном возрасте.
«Устный счет можно сравнить с навыком скоростной печати на клавиатуре. Сам по себе этот навык почти ни на что не влияет, но облегчает жизнь каждый день, потому что в современном мире мы постоянно что-то печатаем.
В каком возрасте ребенок должен считать в уме
«Оптимальный возраст для начала устного счета – от трех до пяти лет. Можно начать и раньше, если ребенок проявляет интерес к арифметике и довольно быстро осваивает навыки», – подчеркнул преподаватель математики и ментальной арифметики онлайн-школы «Коалиция» Арсений Кузнецов.
Преподаватель Коняев считает, что в среднем ребенок способен считать в уме уже с четырех лет. Однако, по его мнению, торопить события не стоит. «Если это произойдет позже — ничего страшного тут нет. Давить на неразвитый мыслительный аппарат гораздо хуже», – предупредил специалист.
Как научить ребенка складывать и вычитать
Как быстро научить ребенка считать
Изучение цифр, понятий сложения и вычитания дети, как правило, осваивают в дошкольном возрасте…
31 мая 19:54
Сложение и вычитание – базовые арифметические действия, которые дошкольник вполне способен освоить. Арсений Кузнецов советует на первых стадиях производить счет на пальцах, в игровой форме с палочками и картинками.
Арсений Кузнецов советует на первых стадиях производить счет на пальцах, в игровой форме с палочками и картинками.
Дмитрий Коняев поддерживает коллегу в том, что в освоении счета взрослым стоит опираться на игровую механику. «Гуляя по улице, предлагайте ребенку посчитать котов/окна/машины/деревья. Это прекрасный способ вовлечь в игру и развить навык», – объяснил Коняев.
Понятия «больше» и «меньше» также поможет освоить практикоориентированный подход, так как, по мнению специалистов, дети лучше воспринимают информацию, которая проецируется на реальную жизнь. «Первое время можно объяснять на примере конфет, кубиков, раскладывая большее количество в правую сторону, меньшее – в левую. Так у ребенка возникнут ассоциации, что меньшее число всегда находится левее», – рассказал Кузнецов. Он отметил, что ребенка важно обучить последовательности счета, и тогда с крепким фундаментом знаний дошкольнику будет проще переходить на более высокие уровни сложности.
close
100%
Как научить ребенка решать примеры с переходом через десяток
«Дети начинают чувствовать себя растерянно, когда помимо привычных примеров, где ответ получается не более 10, появляются вычисления, выходящие за рамки первого десятка», – поделился наблюдениями преподаватель Кузнецов.
Эксперт посоветовал обратиться к самому комфортному и действенному методу обучения – рисованию схем. Это поможет развеять страх и продемонстрирует, что новые цифры учить не придется, так как все базируется на значениях от 0 до 9.
«При сложении с переходом через десяток нужно дополнять первое слагаемое до 10, а затем прибавлять оставшиеся единицы, – рассказал математик. – Пример: 9 + 7 = ? 9 + 1 + 6 = 16».
Объяснить это ребенку эксперт посоветовал следующим образом: для округления цифры 9 до десятки не хватает 1. Значит, из 7 вычитаем 1 и прибавляем эту единицу к 9, чтобы получить круглое число. После вычитания 1 из 7 осталась шестерка. К 10 прибавляем 6 и находим ответ.
Как научить ребенка считать в уме двузначные числа
До перехода к устному счету необходимо отработать умение складывать и вычитать двузначные числа на бумаге. Эту задачу, по мнению преподавателя Коняева, стоит оставить школе.
Как научить ребенка читать: методики от опытного педагога
Ребенок, который научился читать в три года — гордость родителей. Но стоит ли торопить события и…
Но стоит ли торопить события и…
21 апреля 12:31
Если же родителям не терпится обучить ребенка этому навыку, то можно воспользоваться счетом в столбик. «Столбики дают наглядное представление о десятках и единицах, об операциях, производимых с ними. Когда ребенок начнет безошибочно проводить письменные вычисления, можно приступать к устным расчетам. Стоит начинать с круглых чисел, вычитать из них десятки, затем пятерки, а после усложнять примеры, добавляя в них разнообразия», – рассказал Арсений Кузнецов.
Специалист объяснил, что для освоения навыка дошкольнику может потребоваться больше времени, чтобы он научился представлять в уме ранее используемых столбцов, но занятия каждый день решат эту проблему.
close
100%
Подходит ли ментальная арифметика для обучения быстрому счету
Школы ментальной арифметики сейчас есть почти в любом российском городе, поэтому родителей не может не интересовать вопрос, поможет ли этот метод ребенку научиться быстро считать в уме.
Математик Кузнецов порекомендовал осваивать этот метод тем, кто готов к немалому вложению энергии и времени. Также обучение потребует от дошкольника терпения. Но наградой за труды станет способность к высокой концентрации внимания, гибкость мышления и памяти.
«Ментальная арифметика направлена на развитие умственных способностей ребенка и мелкой моторики рук. За данной методикой обучения скрываются усиленные тренировки и упорство, ее освоение займет около двух лет и первое время будет сопряжено с неверными расчетами. Сдвиги в лучшую сторону начнутся после пары месяцев занятий», – отметил эксперт.
Он объяснил, что для освоения ментальной арифметики достаточно знать цифры от 0 до 9. Обучение протекает постепенно, и уровни сложности повышаются по мере прохождения предыдущих этапов.
Как научиться быстро считать в уме? — Meduza
1
Зачем в уме, когда можно на калькуляторе или в столбик?
Минимальные навыки счета, чувство числа — такой же элемент общечеловеческой культуры, как грамотное письмо и речь, владение иностранным языком, базовое представление об искусстве и окружающем мире.
Кроме того, когда вы легко считаете без подручных средств, вы чувствуете совершенно другой уровень управления реальностью — вы заранее знаете, сколько сдачи вам дадут в магазине или стоит ли набиваться всемером в лифт грузоподъемностью 400 килограммов.
Подумайте и о том, что калькулятор и действия в столбик — это же такая разновидность магии. Скорее всего, вы не понимаете, как это работает, и вынуждены просто доверять им. А когда вы хорошо понимаете, как устроены математические операции и можете их воспроизвести «руками», ваше чувство контроля (и уверенности в себе) получает серьезный бонус.
И наконец, устный счет развивает ваши ментальные способности: внимание, память, концентрацию, переключение между несколькими потоками мышления, а также может послужить средством для медитации или отвлечения от грустных мыслей.
2
Но где брать задания для тренировки? Самому себе примеры придумывать?
Конечно, нет. В сети полно мобильных приложений, которые предложат вам тренировку математических навыков на любой вкус.
При выборе учтите, что хорошее приложение, как минимум, должно обладать достаточно гибкими настройками сложности и вести статистику решенных вами заданий.
Попробуйте эти приложения под iOS и Android или поищите альтернативные варианты в App Store и Google Play.
3
А как именно нужно тренироваться?
Основных математических действий всего четыре — сложение, вычитание, умножение и деление. У каждого действия есть свои особенности, но они не сложные. Надо один раз разобраться, а потом тренироваться минут по 5−10 в день, и очень скоро вы почувствуете, что считаете лучше. Скорее всего, за два-три месяца вы выйдете на достаточно приличный уровень, который можно будет поддерживать эпизодическими тренировками.
4
И с чего же начать?
Начните с самого простого уровня — сложения однозначных чисел, и доведите его до совершенства: 99% правильных ответов, на каждый ответ 1−2 секунды. Для решения примеров «с переходом через 10» попробуйте использовать следующую технику — «Опора на десяток».
Допустим, вам нужно сложить 8 и 7.
1) Спросите себя, сколько числу 8 не хватает до 10 (это 2).
2) Представьте 7 как сумму 2 и какого-то второго кусочка (это 5).
3) Прибавляйте к 8 сначала ту часть числа 7, которой недоставало до 10, а потом тот второй кусочек — получится 10 и 5, и это, конечно, 15.
5
Как складывать многозначные числа?
Здесь самый важный принцип — это сложение одинаковых разрядов друг с другом. Разбив оба числа на «разрядные части», начните складывать со старших разрядов — тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами. То, что получится, при необходимости укрупняйте и снова считайте все вместе.
Например, как сложить 456 и 789?
1) 456 состоит из трех разрядных частей — 400, 50 и 6.
789 тоже разбивается на три разрядные части — это 700, 80 и 9.
2) Складываем сотни с сотнями: 400+700 = 1100, десятки с десятками: 50+80 = 130, единицы с единицами: 6+9 = 15.
3) Укрупняем, разбивая на удобные части, снова группируем и складываем одинаковые разряды: 1100+130+15 — это 1100+100+30+10+5, то есть, 1200+40+5 = 1245.
Поправка. При сложении разрядов мы перепутали единицы и к 6 прибавили 8 вместо 9. В итоге сумма тоже оказалась неправильной — 1244 вместо 1245. Приносим извинения за ошибку, и не повторяйте ее — внимательно следите за числами, особенно в устном счете!
6
Что насчет вычитания?
И здесь надо начинать с базового уровня — вычитания однозначного числа из чисел первого и второго десятка — и довести этот навык до совершенства. Как и в случае сложения, проблемы обычно возникают с вычитанием «с переходом через 10». И здесь поможет аналогичный способ «опоры на десяток».
Допустим, нам нужно из 12 вычесть 8.
1) Спросим себя, сколько нужно отнять от 12, чтобы получилось 10 (это 2).
2) Будем из 12 вычитать 8 по частям — сначала вычтем эту 2, а потом все остальное. А остальное — это сколько? (это 6).
3) После вычитания 2 из 12 мы получили 10, и нужно вычесть еще 6, получится 4. Готово!
7
А что с многозначными числами? С ними все сложно?
Не особенно.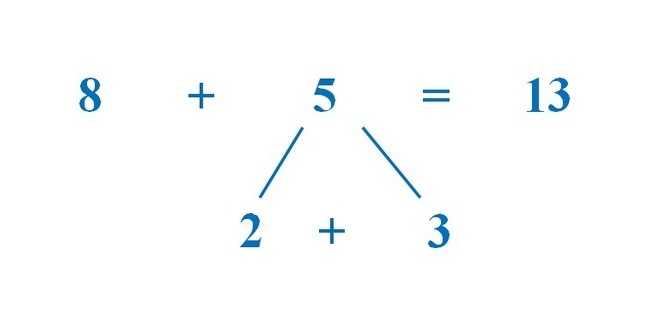 Важно только не путать технику вычитания с техникой сложения. При сложении нам было удобно разбивать каждое из чисел на разрядные части, а здесь мы разбиваем только то число, которое вычитаем.
Важно только не путать технику вычитания с техникой сложения. При сложении нам было удобно разбивать каждое из чисел на разрядные части, а здесь мы разбиваем только то число, которое вычитаем.
Итак, допустим, нам нужно вычесть 512−259.
1) Число 259, которое мы вычитаем, состоит из трех разрядных частей — 200, 50 и 9. Их-то по очереди мы и вычтем.
2) 512−200 — вычитание сотен никак не затрагивает десятков и единиц числа 512, влияет только на сотни, так что результат будет такой — 312.
3) Из того, что получилось после вычитания сотен, теперь вычтем десятки, 312−50.
Это похоже на вычитание через десяток. Вычтем из 312 сначала 10 до целых сотен (единицы не будут затронуты), получим 302. А потом вычтем все остальное (всего нужно было вычесть 50, 10 уже вычли, осталось вычесть 40), получается 262.
4) Осталось вычесть единицы: 262−9.
Чистый переход через десяток — вычитаем сначала 2, получим 260, а потом вычитаем остальную часть, 7, получаем 260−7 = 253. Вот и ответ.
Вот и ответ.
8
Как устроено умножение?
Начнем с умножения однозначных чисел. Для начала нужно вспомнить, что умножение — это когда несколько раз складывают одно и то же. Например, умножить 4 на 7 означает сложить четыре семерки. Пользуясь техникой сложения, мы можем легко посчитать — две семерки, 7 и 7, будет 14, если еще добавить третью 7, получится 21, и, добавляя последнюю, четвертую семерку, в результате получим 28.
Постепенно в результате тренировок вы запомните удобные вам опорные значения умножения и с их помощью сможете быстрее вычислять соседние. Например, если нужно умножить 6 на 7 (то есть, сложить шесть семерок), а вы помните, что 5 умножить на 7 (то есть, сложить пять семерок) будет 35, то чтобы получить итоговый результат, нужно просто добавить шестую семерку — получится 42.
Самым сложным примером в таблице умножения считается 7∙8. Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.
9
Как умножать многозначное число на однозначное?
Разберем на примере. Допустим, нам нужно умножить 468 на 6.
1) 468 состоит из 400, 60 и 8, и все это нужно умножить на 6. Что ж, по отдельности эти задачи не сложнее умножения однозначных чисел.
2) Идем от старшего разряда к младшему: 400∙6 = 2400 (поскольку 400 в 100 раз больше, чем 4, то и результат 400∙6 будет в 100 раз больше, чем результат 4∙6).
Соответственно, 60∙6 = 360, а 8∙6 = 48.
3) А теперь, как при сложении, складываем все это вместе, группируя одинаковые разряды:
(2000+400)+(300+60)+(40+8) = [перегруппируем] =
= 2000+(400+300)+(60+40)+8 = [сложим одинаковые разряды] =
= 2000+700+100+8 = [сгруппируем и сложим одинаковые разряды] =
= 2000+800+8 = [дальше укрупнять нечего, получаем ответ] = 2808.
10
Как перемножать двузначные числа?
Для обычного человека это уже высший пилотаж! Если вы освоили умножение двузначных, считайте, что вы приняты в мир элиты устного счета.
Итак, например, умножим 78 на 56. Это означает, что нам нужно число 78 сложить («взять») 56 раз.
1) Эти 56 раз можно разбить на этапы — сначала 78 сложим 50 раз, потом 6 раз, а потом объединим результаты.
2) Число 78 сложить 50 раз несложно — это в 10 раз больше, чем сложить его 5 раз. 78∙5 = 70∙5+8∙5 = 350+40 = 390. А значит, 78∙50 = 3900, запомним это число.
3) Теперь посчитаем 78∙6 = 70∙6+8∙6 = 420+48 = 468.
4) Ну а теперь сложим вместе оба результата: 3900+468 = 3000+900+400+60+8 = 3000+1300+60+8 = 4368. Вуаля!
Поправка. На заключительном этапе при сложении 3900 и 468 мы неправильно разбили второе число на разряды — забыли про 60. В итоге в сумме получилось 4308. Приносим извинения за ошибку, и не повторяйте ее — нельзя терять в устном счете слагаемые.
11
Ничего себе, осталось последнее только действие, деление?
Да, мы на финишной прямой. И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
Итак, что же такое деление? По сути, это «обратная» операция к умножению.
Например, разделить 56 на 7 — значит подобрать такое число, что если его умножить на 7, то получится 56. Поскольку вы к этому моменту уже хорошо ориентируетесь в таблице умножения, то наверняка вспомните, что именно 8, умноженное на 7, дает 56. Значит, искомое число — это 8, 56:7 = 8.
И так всегда — вспоминайте, какое число при умножении дает нужный результат — это и есть то число, которое вам нужно.
12
Как делить многозначные числа на однозначное?
Давайте разделим 6144 на 8. Наш способ — «отрезать» от исходного числа максимальные «круглые» части, каждая из которых будет гарантированно делиться на 8 по таблице умножения.
1) Выделим из 6144 как можно большую часть, которая делится на 8 по таблице умножения. Это будет 5600, ведь 56 делится на 8, а следующее число, которое делится на 8 — это уже 64, что нам не подходит, так как 6400 больше, чем 6144. Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).
Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).
По ходу дела будем делить:
6144:8 = [выделяем максимальную удобную круглую часть] =
= (5600+544):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 700+544:8.
700 запомним как частичный результат, а сами займемся делением 544:8.
2) Аналогично, из числа 544 самая большая часть, которую можно удобно разделить на 8 по таблице умножения, это 480 (ведь 48 делится на 8, а следующее число — 56 — нам не подходит, т. к. 560 > 544). Итак, 544 = 480+64.
Продолжаем деление:
544:8 = [выделяем максимальную удобную круглую часть] =
= (480+64):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 60+64:8.
60 добавим к 700, 700+60 = 760 — запомним это как вторую часть результата и перейдем к последнему делению, 64:8.
3) Оставшийся кусочек, 64, тоже делится на 8 по таблице умножения, 64:8 = 8.
Соответственно, полный результат деления — это 760+8=768. Все!
Все!
13
Как делить на двузначное число?
Техника деления на двузначное число — самая разнообразная, непохожая ни на что, изысканная. Познакомимся с ней на примере 5148:66.
1) Подгадаем, в каком десятке лежит наш результат. Напомним, что 5148:66 означает: мы ищем число, которое при умножении на 66 даст 5148. Будем использовать технику «пристрелки».
Просто наугад попробуем число 20 как возможного кандидата. 20∙66 = 1320, это раза в 4 меньше, чем 5148, которое нам нужно.
В 4 раза больше, чем 20 — это 80, попробуем его. 80∙66 = 5280, получилось больше, чем нужное 5148, но немного, скорее всего, это «верхний» десяток.
Проверим для надежности 70, предыдущий перед 80 десяток. 70∙66 = 4620, это как раз меньше 5148, отлично! Значит, число, которое мы ищем, лежит между 70 и 80.
2) Воспользуемся математическим законом о последней цифре результата умножения двух чисел.
Оказывается, она всегда совпадает с последней цифрой результата умножения последних цифр этих чисел (попробуйте подумать, почему это так). Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Поэтому, если мы ищем число, которое при умножении на 66 даст 5148, то чтобы гарантировать эту 8 на последнем месте, искомое число может заканчиваться только либо на 3, либо на 8 (3∙6 = 18, 8∙6 = 48).
3) С такими окончаниями между 70 и 80 у нас два всего кандидата — 73 и 78.
5148 явно ближе к 5280, поэтому сперва проверим 78.
78∙66 = 78∙60+78∙6 = 4680+468 = 5000+148 = 5148, ура!
(Ну а если бы результат не сошелся, то мы бы проверили второе число, и оно бы уже точно подошло).
14
Какие рекомендации напоследок?
Вот, в общем-то, и все способы, которые достаточно знать для тренировки уверенного счета в пределах 10000 (а умение работать в уме с большими числами, пожалуй, уже выходит за рамки необходимого общего развития).
Наверняка вы также столкнетесь с другими приемами, т. н. «хитростями» быстрого счета, но не торопитесь увлекаться ими. Кроме того, помните, что регулярность важнее интенсивности — старайтесь заниматься на тренажере каждый день по 5−10 минут, больше не нужно, иначе велик риск «перегореть» и забросить.
В процессе занятия никуда не торопитесь — ловите свой ритм, делайте упор на правильность ответов, а не на скорость, скорость придет потом.
Обязательно пробуйте проговаривать свои действия вслух, особенно на первых порах — у вас будет шанс почувствовать, как все это похоже на стихи, да и решать так будет проще.
И не расстраивайтесь, если что-то не выходит — дорогу осилит идущий, и рано или поздно у вас точно все получится.
Стратегии и советы по ментальной арифметике, которые должен знать каждый ребенок
Когда мы думаем о стратегиях ментальной арифметики, мы в основном думаем о тех математических навыках, которые мы можем выполнять в уме, не используя формальные письменные методы, которые мы использовали бы для более длинных вопросов и стандартные методы алгоритма.
В этой статье мы познакомим вас с некоторыми стратегиями ментальной арифметики, которым вы можете научить своих учеников, чтобы развить их навыки ментальной арифметики в начальной школе.
Что такое математические стратегии в уме?
Стратегии ментальной арифметики — это общепринятые способы решения математических задач в уме, которые помогают нам срезать путь и эффективно находить правильный ответ.
Почему важны математические стратегии в уме?
Стратегии ментальной математики лежат в основе большинства областей математики, в которых используются числа. Без эффективных умственных стратегий дети часто не могут быстро и бегло считать.
Умственные стратегии также являются основой любого письменного или формального метода в математике. Ссылаясь на это как на умственную математику, это не означает, что вы вообще ничего не можете записать, но любая письменная работа будет представлять собой быстрые наброски, помогающие запомнить через многошаговые задачи.
По мере того, как дети начинают использовать более формальные методы, начиная примерно с 3-го класса, и по мере того, как числа, с которыми они работают, становятся все более ценными, навыки ментальной математики жизненно важны для обеспечения беглости и точности в математике.
Развитие истинного беглого владения математикой
Эффективные умственные стратегии важны, если дети хотят развить «истинное» беглое владение математикой
Истинное беглое владение языком можно лучше всего определить как способность детей уверенно использовать и применять свои знания о числовых отношениях, числовых фактах и наших знаниях. систему счисления для вычисления и решения задач.
Стоит помнить, что свободное владение математикой не ограничивается способностью вспоминать известные факты. Точнее, важно то, как дети могут использовать и применять эти факты, в том числе с помощью ряда умственных математических стратегий.
«Отстающие часто являются отстающими не потому, что знают меньше, а потому, что не умеют гибко использовать числа». – Джо Боалер
– Джо Боалер
Индивидуальное онлайн-обучение Third Space Learning в значительной степени направлено на формирование у учащихся уверенности и свободного владения математикой. Наши еженедельные уроки с репетиторством, разработанные с учетом индивидуальных потребностей каждого ребенка, направлены на то, чтобы укрепить понимание учениками числовых фактов и способов их применения в широком круге вопросов.
Использование числовых фактов для решения больших вычислений на онлайн-уроке математики третьего класса Space Learning во 2-м классе.Будьте осторожны, чтобы не ошибиться в названиях математических навыков в уме.
При работе над развитием «истинной» беглости речи важно помнить, что точность — это не то же самое, что беглость речи.
Например, рассмотрим следующие сценарии, которые, хотя и являются точными, не обязательно могут быть классифицированы как беглые:
- Первоклассник вычисляет 40 + 8, считая единицами;
- Третьеклассник, вычисляющий 1003 – 998 формальным письменным методом;
- Пятиклассник вычисляет 41,79 + 25,3 + 25,7 – 41,79сложив первые три числа, а затем вычтя четвертое.

Этот отрывок из исследовательской работы «Развитие вычислительной беглости с целыми числами», опубликованной в 2000 году С. Дж. Расселом, остается одним из лучших объяснений беглости:
«Беглость опирается на хорошо построенную математическую основу, состоящую из трех частей:
- понимание смысла операций и их отношения друг к другу — например, обратное отношение между умножением и делением;
- знание большого набора числовых отношений, включая «факты» сложения и умножения, а также другие отношения, например, как 4 × 5 связано с 4 × 50;
- и глубокое понимание системы счисления с основанием 10, того, как числа устроены в этой системе, и как система разрядов чисел ведет себя в различных операциях — например, что 24 + 10 = 34 или 24 × 10 = 240′ .
Быстрое вспоминание и вычисления в уме с заметками
Когда мы обсуждаем вычисления в уме в математике в старших классах начальной школы, нам нужно четко понимать различие между фактами, которые дети должны уметь быстро вспоминать, и типами вычислений, которые дети должны уметь производить в уме, иногда с помощью заметок.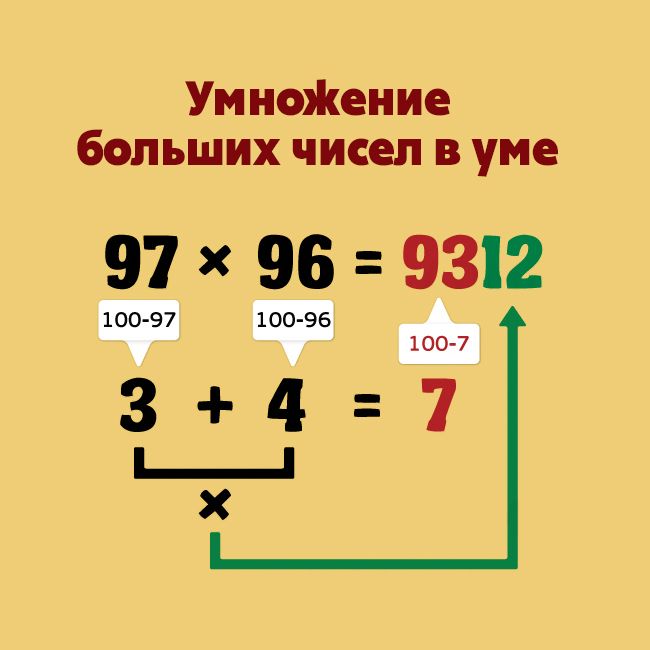
Практика припоминания и быстрого припоминания числовых фактов важна, потому что, если дети способны автоматически вспоминать числовые факты, это позволяет им высвободить свою рабочую память при столкновении с более сложными вопросами.
Они также способны более эффективно и точно решать проблемы, рассуждать и устанавливать связи, если им не приходится постоянно вычислять одни и те же «базовые» факты.
«Обучая процедурным и фактическим знаниям, убедитесь, что учащиеся доходят до автоматизма. Объясните учащимся, что автоматизм [с ключевыми фактами] важен, потому что он освобождает их разум для размышлений о концепциях». – Дэниел Уиллингем – когнитивист, в теме «Правда ли, что некоторые люди просто не умеют считать?»
Концепция должна быть понята, прежде чем вводить стратегию
Прежде чем мы сможем ожидать быстрого припоминания и автоматизма числовых фактов с нашими стратегиями ментальной математики, нам необходимо научить основным математическим концепциям. Например, только когда у детей есть надежное концептуальное понимание числовых связей до 10, следует пытаться быстро вспоминать.
Например, только когда у детей есть надежное концептуальное понимание числовых связей до 10, следует пытаться быстро вспоминать.
Исходя из этого понимания числовых связей до 10, можно использовать стратегию разделения. Например, к 5-му классу большинство детей должны уметь вычислять в уме 34 х 5 (30 х 5 + 4 х 5), используя разбиение и свои знания закона распределения, подкрепленные базовыми вычислениями.
Хотя учащиеся будут запоминать все больше и больше математических фактов, которые они смогут запомнить «наизусть», жизненно важно, чтобы они понимали концепции. Работа с манипуляторами может помочь в этом, переходя к виртуальным манипуляторам на интерактивной доске, когда числа становятся слишком большими, чтобы удерживать их физически.
Оценка математических стратегий в уме, которые использует ваш класс
Один из действительно интересных способов проверить стратегии в устной арифметике – представить группам разные письменные версии одних и тех же математических задач.
- Представьте одну задачу
Если вы представите задачу, например 64 + 17, в предложении, подобном этому, те дети, которые уверены в своих математических стратегиях в уме, решат ее в уме.
Обычно они, даже подсознательно, если говорят бегло, разбивают числа и вычисляют 60 + 10, а затем 4 + 7, или 60 + 17, затем прибавляют 4. Некоторые делают 64 + 10, а затем прибавляют 7.
Некоторые могут округлять числа, например, 64 + 20, используя числовые связи, до 20 знаний, а затем минус 3.
Некоторые могут снова использовать свои числовые связи, чтобы вычислить 64 + 17, добавив 63 + 17, чтобы получить 80, а затем добавить 1.
Вы ожидаете, что ваш класс даст ряд ответов относительно своего метода, но, надеюсь, все говорят бегло. и может найти правильный ответ, не более чем быстро записывая некоторые числа при добавлении нескольких шагов.
- Создайте две версии одного и того же набора из 10 вопросов
Теперь составьте лист из 10 похожих вопросов с диапазоном сложения и вычитания, которые, как вы ожидаете, ваш класс сможет выполнить в уме. Создайте вторую версию этого, которая излагает те же вопросы, с теми же точными числами и тем же ожидаемым ответом, в стандартном формате метода алгоритма.
Создайте вторую версию этого, которая излагает те же вопросы, с теми же точными числами и тем же ожидаемым ответом, в стандартном формате метода алгоритма.
Дайте половине класса первый лист в виде числового предложения, а другой половине — вторую версию, где вопросы представлены в формате стандартного метода алгоритма.
Не говорите группам, что у них разные листы, и раздавайте их за разные столы, чтобы они не видели другой формат тех же вопросов. Дайте им время, чтобы они индивидуально ответили на вопросы и записали свои ответы.
- Попросите детей поделиться своими методами
Ответьте на первый вопрос и попросите кого-нибудь добровольно поделиться своим методом. Затем попросите кого-нибудь поделиться, затем еще кого-нибудь и так далее. Убедитесь, что вы получили пару примеров из таблиц с горизонтальным расположением вопросов и пару примеров из таблиц с вертикальным расположением столбцов.
Вы, скорее всего, обнаружите, что группы, у которых была горизонтальная схема, с гораздо большей вероятностью просто обдумывали это в уме, в то время как группы, у которых была вертикальная схема, тратили время на поиск и запись ответов по стандартному алгоритму. включая каждый шаг, хотя они могли бы легко решить эти задачи в уме.
включая каждый шаг, хотя они могли бы легко решить эти задачи в уме.
Это упражнение является прекрасным напоминанием о том, что даже когда мы видим формальные вычисления, мы должны использовать наши стратегии ментальной математики, чтобы ускориться там, где мы можем.
Укрепление уверенности в умственных математических стратегиях
При введении любого нового математического понятия — от сложения до процентов и десятичных дробей — детям будет полезно показать физическое представление чисел (с использованием математических манипуляций) и операций перед использованием графических представлений (например, числовые линии или модели столбцов), а затем, наконец, написанные методы с использованием символов числа и операции.
Подробнее: Конкретный иллюстрированный абстрактный метод
По пути вам нужно будет много раз повторять и тренироваться вспоминать факты в уме. Мы надеемся, что по мере того, как дети становятся старше и переходят в старшие классы начальной школы, переход от физического к письменному будет происходить быстрее для новых концепций, поскольку они строятся на прочном фундаменте.
Разные дети могут переходить к умственным стратегиям в разных точках каждого блока. Некоторые могут перейти от физического к ментальному, если они быстро схватывают концепцию и уже имеют четкое понимание.
Другие могут не достичь беглости запоминания и применения до тех пор, пока они не попрактикуются в написании ответов и не укрепят уверенность в этих новых числовых фактах и стратегиях.
Возможно, вам также придется распаковать любые неправильные представления на этих этапах, и это может включать возвращение «назад» к физическому. Хорошей практикой является всегда иметь под рукой манипуляторы во время выполнения самостоятельных заданий, даже в 5-м классе и для всех способностей. Иногда быстрое сравнение с использованием палочек с основанием 10 или палочек Кюизенера может помочь ребенку «закрепить» эту стратегию в голове.
Также важно не учить детей выполнять математические трюки, например, «прибавлять ноль» при умножении на десять, так как это может вызвать проблемы в более позднем возрасте с пониманием разрядности. Однако можно надеяться, что дети заметят такие закономерности в своих ответах, и это должно привести к обсуждению и сравнению, а также предоставить детям возможность проверить свою теорию там, где они заметили возможную закономерность. Даже если вы знаете, что это неправильно/правильно, они выиграют от возможности проверить и применить это предположение.
Однако можно надеяться, что дети заметят такие закономерности в своих ответах, и это должно привести к обсуждению и сравнению, а также предоставить детям возможность проверить свою теорию там, где они заметили возможную закономерность. Даже если вы знаете, что это неправильно/правильно, они выиграют от возможности проверить и применить это предположение.
Подробнее: Математические приемы, которых следует избегать и умственный труд, арифметика и рассуждение. Они фактически формируют прогрессию, начиная с 3-го класса, поэтому важно, чтобы в детском саду – 2-м классе уже была сделана основа, чтобы дети могли выполнять вычисления в уме.
Таким образом, эти навыки лучше всего рассматривать как прогрессию, а не как набор ожиданий годовой группы.
Как улучшать математику в уме год за годом
Наряду с расширением диапазона детских вычислений в уме по мере прохождения ими элементарных предметов, следите за тем, чтобы они каждый год получали достоверные данные.
Как развить в уме математические стратегии, необходимые для сложения и вычитания
В младших классах дети узнают основные сведения о числах, включая сложение и вычитание. Это будет включать количество облигаций до 20 к тому времени, когда они закончат 1-й класс. Они будут много работать с физическими объектами и играть в ролевые игры, поэтому в эти годы хорошей практикой является не только практиковать математические навыки во время уроков математики, но и создавать возможности для вопросов вне этих уроков.
Попросите детей подсчитать, сколько учеников сегодня отсутствовало, посчитав карандаши на каждом столе, чтобы увидеть, достаточно ли у них (или слишком много, или слишком мало), и пополнить словарный запас на уроках математики.
Как только дети усвоят концепцию фактов сложения и фактов вычитания, а также то, что они являются обратными операциями (хотя они могут еще не знать этого конкретного слова), они начнут укреплять свое быстрое запоминание числовых связей и применять их в своей работе.
Также никогда не рано вводить различные стратегии для отработки своих расчетов, если базовое понимание правильное. Спросить их, есть ли другой способ, которым они могли бы найти ответ, можно задать на официальных уроках, в ролевой игре или в спорте.
Основные факты сложения, которые дети должны знать ко 2-му классуСтратегии сложения и вычитания в уме в старших классах
Счет в прямом и обратном порядке
Счет в прямом и обратном порядке впервые встречается в младших классах, начиная с единицы и считая до единиц .
Чувство числа у учащихся расширяется за счет того, что они начинают с разных чисел и считают в прямом и обратном порядке не только единицы, но и двойки, пятерки, десятки, сотни, десятые и так далее.
Прогресс в счете в прямом и обратном порядке
Вот способы, которыми вы можете помочь своему классу прогрессировать в счете в прямом и обратном порядке:
- Счет в десятки и обратно от любого числа (например, работая над 27 + 60= ? путем подсчета десятками от 27)
- Счет до пятерок или обратно от любого числа, кратного 5 (например, 35+15=? путем счета с шагом 5 от 35.
 )
) - Счет до сотен или обратно от любого числа (например, 570 + 300= ?, считая сотни от 570.)
- Счет вперед или назад в десятых и/или сотых долях (например, 3,2 + 0,6 = ? при счете в десятых долях. 1,7 + 0,55=? в счете в десятых и сотых долях.)
Разбиение для сложения и вычитания
Стратегии разбиения учат детей разбивать большие числа на меньшие.
Важно, чтобы дети знали, что числа могут быть разделены – как по границам разрядного значения (канонически), так и другими способами (неканонически).
Затем они могут использовать свое разбиение, чтобы помочь им в вычислениях сложения и вычитания. Это может быть расширено по мере того, как дети продвигаются по старшим начальным классам.
Прогресс в делении на части
Вот как вы можете помочь своему классу в делении на части:
- Вычисления с целыми числами, не требующие пересечения границ разрядных значений. Например. 23 + 45= ? на 40 + 5 +20 + 3 или 40 + 23 + 5
- Вычисления с целыми числами, включающие пересечение границ разрядного значения.
 Например. 49– 32= ? на 49 – 9 – 23 или 57 + 34 = ? на 57 + 3 + 31
Например. 49– 32= ? на 49 – 9 – 23 или 57 + 34 = ? на 57 + 3 + 31 - Вычисления с десятичными числами, не связанные с пересечением границ разряда 5.6 + 3.7= ? на 5,6 + 3 +0,7 или 540 + 380= ? на 540 + 300 + 80 или 540 + 360 + 20
- Вычисления с десятичными числами, которые включают пересечение границ разрядного значения. Например. 1,4 + 1,7= ? на 1,4 + 0,6 + 1,1 и 0,8 + 0,35 = ? на 0,8 + 0,2 + 0,15
Компенсация и корректировка
Компенсация заключается в том, чтобы добавить больше, чем нужно, а затем вычесть лишнее.
Эта стратегия полезна для сложения чисел, близких к кратным 10, например чисел, оканчивающихся на 1 или 2, 8 или 9.
Добавляемое число округляется до кратного 10 плюс или минус небольшое число.
Например, добавление 9 выполняется путем прибавления 10, а затем вычитания 1. Аналогичная стратегия работает для добавления десятичных дробей, близких к целым числам.
Вот как вы можете помочь своему классу добиться прогресса в компенсации и корректировке:
- Компенсация и настройка на 10.
 (например, 34 + 9=? на 34 + 10 – 1 или 34 – 11= ? на 34 – 100 – 1 = ?)
(например, 34 + 9=? на 34 + 10 – 1 или 34 – 11= ? на 34 – 100 – 1 = ?) - Компенсация и настройка, кратные 10. (например, 38 + 68 = ? на 38 + 70 – 2 или 45 – 29 = 45 – 30 + 1)
- Компенсация и корректировка, кратные 10 или 100. (например, 138 + 69= ? на 138 + 70 – 1 или 299 – 48 = 300 – 48 – 1)
- Компенсация и корректировка кратных с десятичными дробями. (например, 2 ½ + 1 ¾ на 2½ + 2 – ¼ или 5,7 + 3,9 на 5,7 + 4,0 – 0,1)
Расчет с использованием почти двойных чисел
Когда дети автоматически вспоминают основные двойные факты, они могут использовать эту информацию при сложении двух чисел, которые очень близки друг к другу.
Вот способы, которыми вы можете помочь своему классу прогрессировать в почти двойных числах:
- Почти двойные числа до 20. Например. 18 + 16 равно удвоению 18 и вычитанию 2 или удвоению 16 и прибавлению 2.
- Почти удвоение числа, кратного 10. 60 + 70 — это удвоить 60 и прибавить 10, или удвоить 70 и вычесть 10, или 75 + 76 — это удвоить 76 и вычесть 1, или удвоить 75 и прибавить 1.

- Десятичное число почти удваивается до целых чисел. Например. 2,5 + 2,6 — это удвоить 2,5, добавить 0,1 или удвоить 2,6, вычесть 0,1.
Как разработать математические стратегии в уме, необходимые для умножения и деленияПо мере прохождения начальной школы учащиеся узнают факты умножения. Им потребуется свободное владение фактами умножения, чтобы они могли вспомнить их достаточно быстро для проверки сейчас и в высшем образовании. Опять же жизненно важно, чтобы они понимали концепцию умножения, а не просто повторяли факты наизусть.
Тем не менее, практика имеет решающее значение, так как ежедневное вспоминание известных фактов жизненно важно, чтобы новые факты не вытесняли старые там, где они не полностью укоренились.
Дети начинают понимать умножение с помощью удвоения и деления пополам в начальной школе. Это вводит понятия как умножения, так и деления, и они должны начать замечать их закономерности и применять это к математическим вопросам.

Они также узнают факты умножения на 5 и 10, и это начинается со счета вперед и назад в 5 и 10, что они также должны делать с любого заданного числа, а не только с нуля.
Умственные математические факты, которые дети должны знать к концу 3-го классаК концу 3-го класса учащиеся должны уметь запоминать все произведения двух однозначных чисел. А потом в 4 классе факты умножения 11 и 12. Они также должны применять их к задачам со словами и многошаговым задачам по мере повышения уверенности, чтобы убедиться, что они могут применять числовые факты, а не просто повторять их.
Эти навыки счета в уме и их беглость будут иметь жизненно важное значение в тестовых ситуациях. К тому времени, когда они пойдут в старшую школу, они должны иметь очень твердое представление о системе счисления, а также о известных фактах и закономерностях.
38 новых фактов об умножении (и делении), которые дети должны знать к концу 4-го класса. и факты деления на числа, кратные 10 и 100, чтобы мысленно рассчитать увеличивающийся диапазон вопросов на умножение.
Вот способы, с помощью которых вы можете помочь своему классу повысить разрядность:
- Умножить двузначное число на однозначное путем разбиения. Например. 26 х 3 = 20 х 3 + 6 х 3
- Умножение десятичного числа, содержащего до 2 знаков после запятой, на одну цифру путем разбиения. Например. 3,42 x 4 = 3 x 4 + 0,4 x 4 + 0,02 x 4
Стратегии удвоения и деления пополам
Дети должны уметь распознавать деление пополам как результат, обратный удвоению, и уметь быстро вычислять двойные и половинные числа.
Некоторые двойные и половинчатые факты быстро вспоминаются, а не те, которые дети должны вычислять каждый раз, и они описаны в списках выше.
Вот способы, которыми вы можете помочь своему классу прогрессировать в удвоении и делении пополам:
- Найдите двойные и половинные числа любого двузначного числа и любого числа, кратного 10 или 100. (например, половина 680 или двойное 73)
- Умножьте и разделите на 4, дважды удвоив/делив пополам, и на 8, снова удвоив/поделив пополам.
 (например, 34 x 4 = 34 x 2 x 2.)
(например, 34 x 4 = 34 x 2 x 2.) - Найдите двойные числа и половинки любого числа до 10 000 путем разбиения. (например, половина от 32 202 за счет деления вдвое 3000, 2000, 200 и 2.)
- Умножить на 50 путем умножения на 100 и деления пополам. (например, 8 x 50 = 8 x 100 разделить на 2)
- Разделить число, кратное 25, на 25, разделить на 100 и умножить на 4 (путем удвоения и повторного удвоения). (например, 350 ÷ 25 = 350 ÷ 100 x 2 x 2)
- Разделите число, кратное 50, на 50 путем деления на 100, а затем удвоения. (например, 450 ÷ 50= 450 ÷ 10 x 2)
- Двойное и половинное десятичное число с точностью до одного десятичного знака путем деления на порции. (например, половина 8,4 путем уменьшения вдвое 8 и уменьшения вдвое 0,4)
Стратегии вычисления в уме дробей, десятичных знаков и процентовПо мере прохождения начальной школы дети должны лучше понимать дроби, десятичные числа и проценты и то, как они связаны с делением.

Таким образом, к 5-му классу они должны уметь быстро вспоминать факты умножения и деления, чтобы вычислять в уме некоторые вопросы, связанные с дробями, десятичными знаками и процентами.
Вот как вы можете помочь своему классу освоить дроби, десятичные числа и проценты:
- Найдите в уме дроби чисел в таблице умножения на 2, 3, 4, 5 и 10, используя известные факты умножения и деления. (например, 3/5 от 45 на 45 ÷ 5 x 3.)
- Процентные эквиваленты ½, 1/3, ⅕, ⅙, 1/10 и 1/100. (например, ¼ = 25%)
- Найдите 10% или кратные 10% целых чисел и величин. (например, 30% от 50 на 50 ÷ 10 x 3)
- Мысленно найдите 50% путем деления пополам и 25% путем деления чисел и величин на 4 или 2. (например, 25% от 150 на 150 ÷ 4)
Взлом математических вычислений в уме
Этот вирусный твит — очень хороший пример математического трюка в уме. Это также отличный способ использовать математические трюки в уме, чтобы произвести впечатление на своих друзей!
Лучшие советы по ментальной арифметике: как обучать стратегиям ментальной арифметикиМы достаточно подробно рассмотрели вопрос «что», но как на самом деле мы будем обучать стратегиям ментальной арифметики? Вот краткое изложение наших лучших советов:
- Обучайте математическим приемам в уме и методам вычисления в уме, а не просто полагайтесь на то, что дети «соберут их».
 Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связи между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д.
Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связи между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д. - Вовлекайте детей в обсуждение. Детей следует поощрять к обсуждению своих умственных стратегий друг с другом и всем классом, а взрослые в классе должны присоединиться к этому обсуждению. Дети будут видеть и подходить к вычислениям в уме разными (и в равной степени обоснованными) способами, и, делясь ими, они знакомят друг друга с разными способами мышления и «видения» вычисления.
- Обеспечьте регулярную ментальную арифметику. Дети должны иметь регулярную практику умственного счета, которая фокусируется на стратегиях умственного счета. Наряду с обучением стратегиям на основном уроке математики, школы, где дети имеют высокий уровень компетентности и беглости в умственных стратегиях, часто посвящают 15-20 минут в день практике и развитию умственных стратегий и быстрому воспроизведению вне основного урока математики.
 .
. - Не думайте, что тестирование по времени — единственный способ добиться быстрого отзыва. Многие исследования показали, что тестирование на время является одним из наименее эффективных способов развития быстрого припоминания. Вместо этого предоставьте детям множество возможностей использовать, применять и вспоминать факты, которые вы хотите, чтобы они могли быстро вспоминать.
- Играйте в игры и создавайте возможности для значимой деятельности. Если занятия будут веселыми и осмысленными, дети получат поддержку в развитии чувства числа и беглости в увеличивающемся диапазоне вычислений.
- Обеспечьте соблюдение «базовых» числовых фактов. Важно, чтобы вы не пренебрегали «базовыми» числовыми фактами, например, числовыми связями в пределах 10, 20 и 100 и таблицей умножения 1-12x. Часто такие факты, как числовые связи, практикуются только в начальных классах, но жизненно важно, чтобы они практиковались, и детей поощряют использовать эти факты в своих умственных вычислениях.
 Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!
Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!
Подробнее:
- Как преподавать факты умножения, чтобы ученики быстро запоминали
- Что такое свободное владение математикой?
Ссылки:
Рассел, Сьюзан Джо (2007). Развитие вычислительной беглости с целыми числами в начальных классах
Есть ли у вас учащиеся, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.

Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Содержание этой статьи было первоначально написано консультантом по математике и автором Тимом Хэндли, а затем было отредактировано и адаптировано для школ США учителем математики начальных классов Кристи Кулешей.
12 упражнений для улучшения умственных способностей учащихся | Prodigy
Математика в уме не является явной частью большинства учебных программ, но учащихся, которые не могут быстро или автоматически решать относительно простые уравнения в уме, скорее всего, будут бороться с более сложным содержанием.
Но прежде чем ответить на вопрос «Как я могу улучшить свою ментальную арифметику?», полезно знать определение(я) ментальной арифметики.
Ассоциация учителей математики Манитобы определяет умственная математика как:
Комбинация когнитивных стратегий, которая улучшает гибкость мышления и чувство числа.
 Он вычисляет в уме без использования внешних вспомогательных средств памяти. Это улучшает вычислительную беглость за счет повышения эффективности, точности и гибкости.
Он вычисляет в уме без использования внешних вспомогательных средств памяти. Это улучшает вычислительную беглость за счет повышения эффективности, точности и гибкости.Или, с точки зрения учащихся, это:
- Математика в уме
- Математика в уме, быстро и эффективно
- Разминка головы с помощью математики внедрить в операции и процессы
- Математика, которую вы понимаете настолько хорошо, что вам не нужно ничего записывать, чтобы выполнить расчеты/найти ответ младших и средних классах».
Уэйн Уоттс, педагог и автор многочисленных учебников по математике, однажды сказал: «Чувству чисел нельзя научить. Его можно только развивать».
Наука также убедительна.
Подтвержденные исследованиями преимущества вычислений в умеАвторы и права: Джинкс!
Например, часто цитируемое исследование 1-го класса показало, что учащиеся, которые быстро вспоминают сложение фактов, имеют больше когнитивных ресурсов для изучения других навыков и понятий.

В журнале Cogent Education исследователи провели еще одно исследование со 118 учениками 5-го класса, изучая, как вычисления в уме и математические рассуждения влияют друг на друга.
Доказательства были захватывающими:
[Существует] значительная положительная корреляция между вычислениями в уме и математическими рассуждениями. Примечательно, что вместо того, чтобы знакомить учащихся со знакомыми классическими задачами, учащиеся должны иметь возможность решать исключительные/нестандартные задачи, и особенно маленьких детей следует поощрять к умственным вычислениям для развития обоих навыков.
Исследователи Дьюка опубликовали исследование в журнале Clinical Psychological Science о ментальной арифметике с точки зрения здоровья.
Результаты сканирования мозга 186 студентов показали, что вовлечение префронтальной коры головного мозга во время упражнений в уме связано с улучшением эмоционального здоровья.
К счастью, вы уже помогаете учащимся формировать основные математические навыки в уме, когда обучаете округлению, оценке и беглости фактов — развиваете чувство числа, а также то, как они запоминают и воспроизводят шаги и решения.
Пришло время попрактиковаться в умственной арифметике!
Чтобы улучшить то, как ваши ученики строят и практикуют эти математические навыки в уме, попробуйте 12 стратегий, приведенных ниже. Используйте те, которые лучше всего подходят для вас.
1. Знакомство с мнемоническими приемамиУчащиеся, которым трудно овладеть базовыми фактами, могут улучшить свои знания, используя мнемонические приемы, такие как рифмы и аббревиатуры, помогающие запоминать информацию.
В своей магистерской диссертации «Обучение с помощью мнемотехники в классах начальной школы » Арианна Уэйт-МакГоу обнаружила, что учителя понимают положительное влияние, которое это устройство может оказать на учащихся внутри и «за стенами классной комнаты».
Текущие исследования показывают, что пение, движение и общее удовольствие от предмета улучшают процесс обучения и долгосрочное запоминание материала.
 Все эти требования присутствуют при использовании мнемотехники на уроках. Мои исследования подтвердили аналогичные результаты. Все опрошенные учителя отметили более высокий уровень обучения, вовлеченности и веселья при пении песен, основанных на основном материале.
Все эти требования присутствуют при использовании мнемотехники на уроках. Мои исследования подтвердили аналогичные результаты. Все опрошенные учителя отметили более высокий уровень обучения, вовлеченности и веселья при пении песен, основанных на основном материале.В качестве примера возьмем этот мнемонический прием для факта умножения: Мне должно быть 16 лет, чтобы водить пикап 4×4.
Так как они должны быть легко запоминаемыми, помогает, если подсказки включают:
- Рифмы
- Осязаемые объекты или сценарии себя и поделиться ими со студентами, будет полезно, если вы запустите задание, которое заставит их сделать свое собственное.
Им, вероятно, будет легче запоминать созданные ими мнемонические приемы.
2. Читайте книги по математикеСуществует множество книг по математике, которые эффективно контекстуализируют процессы, лежащие в основе решения уравнений, помогая учащимся запоминать их.

В зависимости от возраста ученика рассмотрите:
- В каждом апельсине было 8 ломтиков — Эта книга фокусируется на счете и сложении, предлагая задачи в виде простых для понимания предложений. Он устанавливает новую сцену, наполненную вопросами, с каждым переворотом страницы.
- Гроздья математики — Эта книга, содержащая основные задачи на умножение, представляет собой серию иллюстрированных загадок. Каждая загадка предлагает подсказки и секреты решения определенного уравнения, помогая учащимся улучшить понимание прочитанного наряду с математическими навыками.
- Sir Cumference — В этой серии книг, действие которых разворачивается в средние века, основное внимание уделяется измерениям и геометрии. Время от времени ему помогают его сын и жена Радиус и леди Ди из Аматера, и рыцарь сэр Камференс должен решить математические задачи, представляющие угрозу для его семьи и королевства.

- Секреты ментальной математики — В отличие от детской книги, это руководство обещает «заставить вас мыслить как математический гений в кратчайшие сроки» с помощью «математика-мага» Артура Бенджамина. Поскольку он состоит из более чем 200 страниц, вы можете добиться большего успеха, выбирая ключевые отрывки и читая и применяя математические приемы в уме со своими учениками. Есть также предисловие Билла Ная, ученого парня!
Пока вы читаете книги вслух, ваши ученики могут попрактиковаться в умственном счете. В качестве альтернативы вы можете использовать книги, чтобы использовать преимущества взаимного обучения.
Просто сделайте паузу после определения уравнения, чтобы дать им время поработать над задачами в голове. После того, как они поделятся своими ответами, читайте дальше, чтобы узнать ответ.
3. Предлагайте соответствующие текстовые задачиМногие учащиеся будут более восприимчивы к математическим упражнениям и практике, если материал будет увлекательным.

Дэвид Кембер, профессор учебных программ и педагогики, и его команда опубликовали статью в Активное обучение в высшей школе о мотиваторах обучения студентов.
Опросив 36 студентов бакалавриата, Кембер пришел к выводу:
Одно лишь преподавание абстрактной теории демотивировало. Актуальность может быть установлена посредством: демонстрации того, как теория может быть применена на практике, установления актуальности для местных случаев, соотнесения материала с повседневным применением или поиска применения в текущих новостных выпусках.
Другими словами, если ученики не найдут ваш урок математики актуальным, их мотивация к учебе значительно снизится.
Простой, но эффективный способ оживить контент — создавать математические задачи. Это потому, что вы можете адаптировать вопросы для студентов.
Например, вы можете:
- Ссылка Интересы учащихся — Составляя текстовые задачи с интересами учащихся, вы должны привлечь внимание.
 Если большая часть вашего класса любит бейсбол, проблема измерения может включать дальность броска известного аутфилдера. Использование межкультурных и межпредметных связей помогает укрепить нейронные петли учащихся.
Если большая часть вашего класса любит бейсбол, проблема измерения может включать дальность броска известного аутфилдера. Использование межкультурных и межпредметных связей помогает укрепить нейронные петли учащихся. - Сделайте вопросы актуальными — Задачи со словами, основанные на текущих событиях или проблемах, могут привлечь учащихся, предоставляя четкие и осязаемые способы применения знаний. Студенты не только найдут ваши уроки более интересными, они поверят, что их стоит знать.
- Включить имена учащихся — Назвать персонажей вопроса именами учащихся – это простой способ сделать вопрос понятным и мотивировать класс на решение проблемы.
Вызывая интерес, мотивация учащихся должна повышаться при отработке навыков, важных для ментальной арифметики.
Примечание : Если они борются с мировыми проблемами, научите мнемонику « ЗВЕЗДА »:
S найдите слово задача T переведите слова в уравнение R просмотреть решение
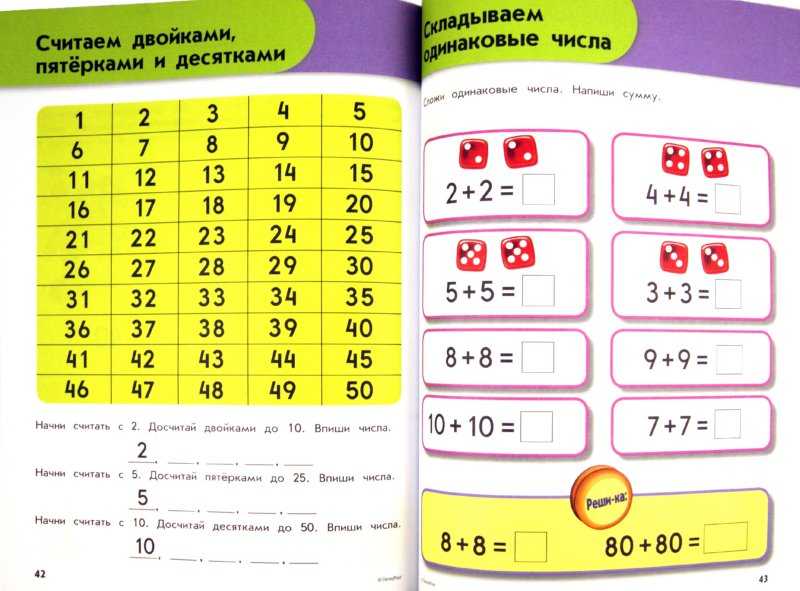
4. Играйте в оценочные игры в классе
Играйте в оценочные игры в классе Оценочные игры — это увлекательные математические занятия, которые побуждают учащихся развивать навыки и методы, которые они могут использовать для упрощения уравнений в уме.
Простая в исполнении, но сложная в игре, популярная во многих классах игра на оценку, в которой используются всего два игральных кубика и лист бумаги, разделенный на две колонки. В одном столбце перечислены значения на каждой грани игральной кости, а в другом — числа по вашему выбору.
Например:
Для игры объедините учеников в пары. По очереди бросая кости, они должны сложить в уме соответствующие числа. Например, если учащийся выбросил пять и шесть, уравнение будет 878 + 777. Без карандаша, бумаги или калькулятора учащийся должен решить уравнение. Если он или она находится в пределах пяти чисел — проверка решения с помощью калькулятора — ответ считается правильным.
Выигрывает тот, кто первым правильно ответит на пять вопросов.

Для более продвинутых классов вы можете упростить числа, но требовать умножения вместо сложения.
5. Играйте в игры на беглость фактов в классеЗабавная альтернатива карточкам, игры на беглость фактов позволяют учащимся развивать навыки запоминания и воспроизведения, важные для умственной арифметики.
Варианты привлечения для 1-8 классов включают:
- Математические факты Бинго — Создавайте карты бинго, которые содержат ответы на различные уравнения. Затем раздайте их учащимся. Вместо того, чтобы звонить по номерам, сформулируйте уравнения, такие как 8 x 7. Определив, что произведение равно 56, они могут отметить число, если оно есть на их карточках.
- Встаньте, сядьте — Выберите номер и поделитесь им со студентами. Затем прочитайте уравнения вслух. Сидя в кругу, учащиеся должны встать, если ответ соответствует выбранному вами числу.
 Если они неправильно стоят или остаются сидеть, устраните их, пока не останется один ученик.
Если они неправильно стоят или остаются сидеть, устраните их, пока не останется один ученик. - 101 и Out — Как следует из названия, цель состоит в том, чтобы набрать как можно больше очков, не превышая 101. Для начала разделите свой класс на группы, раздав каждой по игральному кубику, бумаге и карандашу. Группы по очереди бросают кубик, решая, лучше ли считать число по номиналу или умножить его на 10. После каждого броска число добавляется к общему количеству группы. Игра заканчивается, когда группа набирает 101 очко или перевешивает их — в зависимости от того, что наступит раньше.
Несмотря на то, что они занимаются развитием навыков, улучшение беглости речи у ваших учеников должно быть очевидным после нескольких раундов этих математических игр.
6. Поощряйте использование математических приложений и веб-сайтовВ качестве альтернативы или дополнения к упражнениям и рабочим листам рассмотрите возможность использования цифровой программы, которая предлагает ряд задач, связанных с различными навыками.

Такие математические приложения и веб-сайты побуждают учащихся постоянно отвечать на вопросы в часто увлекательной среде, развивая ряд навыков, важных для ментальной арифметики.
Популярные варианты:
- Prodigy Math — В соответствии с учебными программами по математике во всем англоязычном мире Prodigy автоматически различает контент и дает адаптивную обратную связь, адаптированную для каждого учащегося. Учителя, такие как вы, также могут давать внутриигровые задания для доставки пользовательского контента.
- NRICH — На этом веб-сайте, который является текущим проектом Кембриджского университета, представлены математические игры, статьи и задачи. Он разделяет ресурсы по ключевым этапам в Соединенном Королевстве и уровням обучения в США, что позволяет вашим учащимся легко получать доступ к нужному контенту.
- Math Is Fun — Этот веб-сайт содержит контент, подходящий для учащихся младших классов, с использованием кратких предложений и мультяшных персонажей.
 Помимо упражнений, которые охватывают основные математические навыки, есть игры и головоломки.
Помимо упражнений, которые охватывают основные математические навыки, есть игры и головоломки.
Поскольку для использования этих программ учащимся нужен только компьютер или мобильное устройство, вполне вероятно, что некоторые из них будут добровольно практиковаться дома.
Бесплатный образовательный контент, адаптированный к вашей учебной программе
Сделайте занятия по математике в уме увлекательными с нашим безопасным математическим приключением, соответствующим стандартам!
Откройте для себя Prodigy Math!
7. Округление при умножении на 9Существуют простые способы изменить сложные уравнения, облегчив их решение с помощью арифметики в уме.
Учащиеся могут использовать имеющиеся у них навыки округления и беглого чтения фактов при умножении на 9, 99, 999 и любое число, соответствующее этому шаблону.
Во-первых, попросите учащихся округлить 9 до 10.
 Во-вторых, после решения нового уравнения научите их вычитать число, которое они только что умножили на 10, из ответа.
Во-вторых, после решения нового уравнения научите их вычитать число, которое они только что умножили на 10, из ответа.Например, 67 x 9 приведет к тому же ответу, что и 67 x 10 — 67. Следование порядку операций даст результат 603. Аналогично, 67 x 99 равно 67 x 100 — 67.
Несмотря на большее количество шагов, такое изменение уравнения обычно происходит быстрее и позволяет учащимся завершить его в уме.
8. Удвоение и деление пополамОсваивая умножение помимо основ, учащиеся могут быстро использовать математические навыки в уме для умножения двух целых чисел, когда один из них четное число.
Им просто нужно разделить пополам четное число и удвоить другое число. Они останавливают этот процесс, когда четное целое число нельзя разделить пополам или когда уравнение становится управляемым.
Using 33 x 48 as an example, here’s the process:
- 33 x 48
- 66 x 24
- 132 x 12
- 264 x 6
- 528 x 3
- 1,584
The only предварительным условием для этого умственного математического трюка является понимание таблицы умножения на 2.
9. Сокрытие-копия-сравнение
Обычно используемая в качестве тактики вмешательства, схема «Сокрытие-копия-сравнение» может иметь место на большинстве уроков беглой речи.
Упражнения по арифметике в уме состоят из трех шагов:
- Создание информационного листка по математике — Разделите лист на два столбца и запишите около 10 математических фактов, относящихся к одному и тому же навыку, в левом столбце. Включите числа-предложения и ответы. В правом столбце напишите «Ответы». Раздайте копии листа учащимся.
- Выполнение упражнения — Цель учащихся – изучить математические факты в левой колонке, правильно воспроизведя их в колонке «Ответы». Для этого дайте им время изучить факты. После этого они складывают бумагу, чтобы закрыть левую колонку, записывая — по памяти — первый факт в колонке «Ответы». Если все верно, учащийся может перейти к следующему факту. Если это неверно, учащийся пытается снова, пока он или она правильно не воспроизведет математический факт.

- Запись освоенных навыков — После того, как учащийся заполнит определенное количество листов, связанных с общим навыком, вы можете наградить его или ее значком, обозначающим мастерство навыка. Эта стратегия геймификации может сделать упражнение более увлекательным.
Чтобы выйти за рамки простого беглого чтения фактов, вы можете создавать листы, которые фокусируются на округлении, запоминании шагов для сложных уравнений и многом другом.
10. Используйте подход с записью задач0003 — один из самых эффективных способов для учащихся научиться свободно владеть фактами, — указывает на исследование 2004 года, в котором была впервые применена эта стратегия.Сначала добудьте или сделайте аудиозапись основных математических задач с короткими паузами между постановкой задачи и раскрытием ответа. Во-вторых, дайте каждому ученику карандаш и бумагу.
Во время воспроизведения записи учащиеся должны записать каждое уравнение и попытаться решить его, прежде чем ответ будет раскрыт.
 Если учащийся не может решить вопрос, он или она записывает правильный ответ. Если учащийся дает неверный ответ, он зачеркивает его и пишет правильный ответ.
Если учащийся не может решить вопрос, он или она записывает правильный ответ. Если учащийся дает неверный ответ, он зачеркивает его и пишет правильный ответ.Вы можете удлинить паузы, чтобы учащиеся не зависели от того, услышат ли они ответы, и сократить их, чтобы стимулировать автоматизм.
11. Строительные блокиХотите знать, как повысить скорость счета в уме в своем классе? Познакомьте учащихся со строительными блоками, такими как таблицы умножения или дроби, десятичные числа и эквиваленты процентов.
Чем больше ваши ученики узнают, как выглядит таблица умножения или ее эквиваленты, тем быстрее они смогут распознавать и решать задачи в классе и за его пределами.
Исследование, опубликованное в журнале Journal of Neuro science под названием «Почему арифметика в уме имеет значение: активация мозга при вычислении однозначных чисел предсказывает результаты по математике в средней школе», проверило 33 старшеклассников на их способность решать уравнения на сложение и вычитание.

Все они показали хорошие результаты, что коррелировало с их результатами PSAT по математике. Интересно, как обрисовала нейробиолог доктор Сьюзен Бэрри:
Учащиеся с более высокими баллами PSAT по математике задействовали части мозга, левую надмаргинальную извилину и двустороннюю переднюю поясную извилину, которые были связаны с арифметическим поиском фактов. Напротив, те студенты с более низкими баллами PSAT по математике задействовали правую внутритеменную борозду, область, связанную с обработкой числового количества. Выполняя тест на сканере, 90 003 учащихся с более высокими баллами PSAT по математике больше полагались на свою память на арифметические факты .
12. Number talksРут Паркер, генеральный директор Mathematics Education Collaborative, и Кэти Ричардсон, один из ведущих национальных преподавателей элементарной математики, разработали эту практику ментальной арифметики.
Для начала поставьте абстрактную математическую задачу.
 Возьмите 18 x 5 в качестве примера задачи и попросите своих учеников решить ее в уме.
Возьмите 18 x 5 в качестве примера задачи и попросите своих учеников решить ее в уме.Естественно, в классе из 20+ учеников вы, скорее всего, обнаружите, что они ответили правильно, но по-разному.
Разговоры о числах — отличный способ продемонстрировать, что в математике есть творческий потенциал. Это также отличный способ начать урок математики или побудить родителей заниматься вместе со своими детьми!
В статье «Свободное беглость без страха: данные исследований о лучших способах изучения математических фактов» профессор математического образования и соучредитель Стэнфордского университета вы возвели в куб Джо Боалер пишет:
Исследования говорят нам, что Лучшие классы математики — это те, в которых учащиеся изучают числовые факты и смысл чисел посредством увлекательных занятий, которые сосредоточены на математическом понимании, а не на механическом запоминании.
Итак, мы верим, что эти занятия помогут вашим ученикам практиковать ментальную арифметику в этом учебном году и в дальнейшем.


 )
) Например. 49– 32= ? на 49 – 9 – 23 или 57 + 34 = ? на 57 + 3 + 31
Например. 49– 32= ? на 49 – 9 – 23 или 57 + 34 = ? на 57 + 3 + 31 (например, 34 + 9=? на 34 + 10 – 1 или 34 – 11= ? на 34 – 100 – 1 = ?)
(например, 34 + 9=? на 34 + 10 – 1 или 34 – 11= ? на 34 – 100 – 1 = ?)


 (например, 34 x 4 = 34 x 2 x 2.)
(например, 34 x 4 = 34 x 2 x 2.)
 Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связи между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д.
Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связи между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д.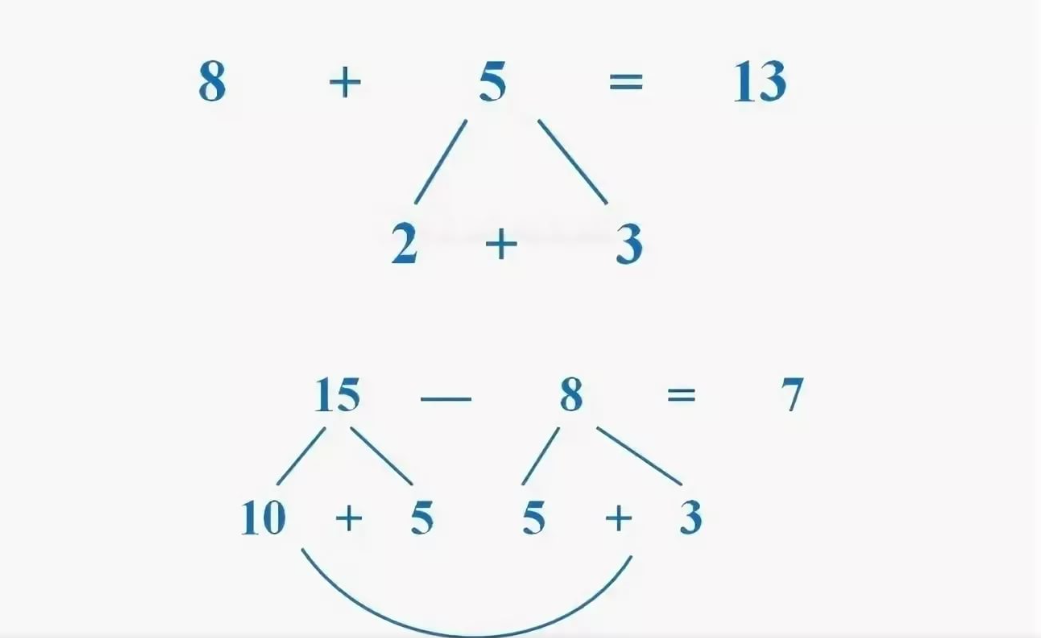 .
. Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!
Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!
 Он вычисляет в уме без использования внешних вспомогательных средств памяти. Это улучшает вычислительную беглость за счет повышения эффективности, точности и гибкости.
Он вычисляет в уме без использования внешних вспомогательных средств памяти. Это улучшает вычислительную беглость за счет повышения эффективности, точности и гибкости.

 Все эти требования присутствуют при использовании мнемотехники на уроках. Мои исследования подтвердили аналогичные результаты. Все опрошенные учителя отметили более высокий уровень обучения, вовлеченности и веселья при пении песен, основанных на основном материале.
Все эти требования присутствуют при использовании мнемотехники на уроках. Мои исследования подтвердили аналогичные результаты. Все опрошенные учителя отметили более высокий уровень обучения, вовлеченности и веселья при пении песен, основанных на основном материале.


 Если большая часть вашего класса любит бейсбол, проблема измерения может включать дальность броска известного аутфилдера. Использование межкультурных и межпредметных связей помогает укрепить нейронные петли учащихся.
Если большая часть вашего класса любит бейсбол, проблема измерения может включать дальность броска известного аутфилдера. Использование межкультурных и межпредметных связей помогает укрепить нейронные петли учащихся. Играйте в оценочные игры в классе
Играйте в оценочные игры в классе 
 Если они неправильно стоят или остаются сидеть, устраните их, пока не останется один ученик.
Если они неправильно стоят или остаются сидеть, устраните их, пока не останется один ученик.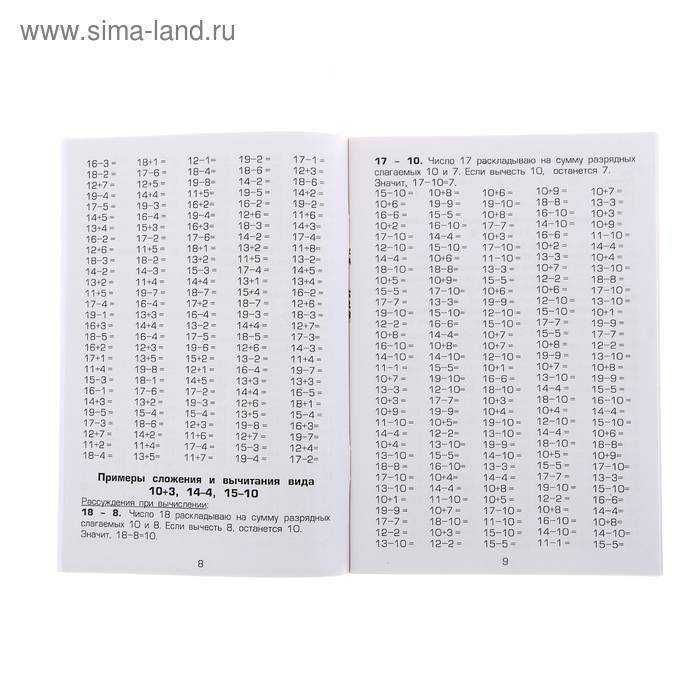
 Помимо упражнений, которые охватывают основные математические навыки, есть игры и головоломки.
Помимо упражнений, которые охватывают основные математические навыки, есть игры и головоломки. Во-вторых, после решения нового уравнения научите их вычитать число, которое они только что умножили на 10, из ответа.
Во-вторых, после решения нового уравнения научите их вычитать число, которое они только что умножили на 10, из ответа.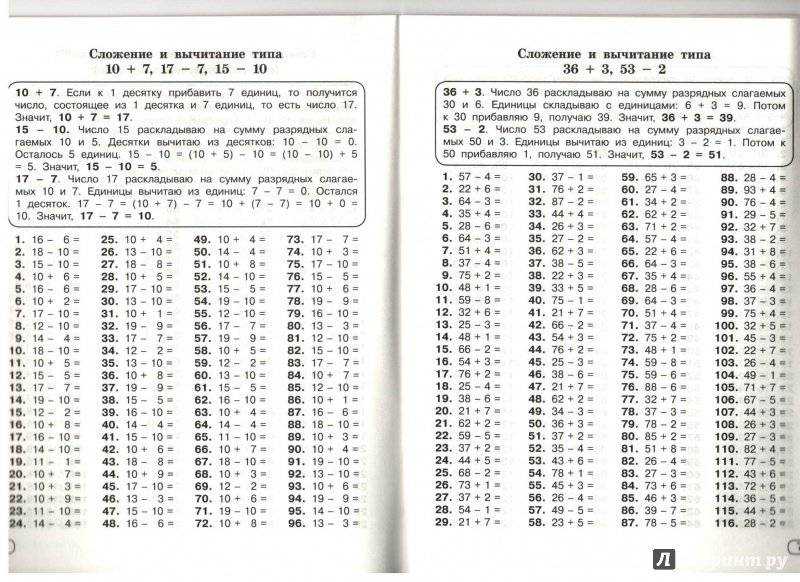

 Если учащийся не может решить вопрос, он или она записывает правильный ответ. Если учащийся дает неверный ответ, он зачеркивает его и пишет правильный ответ.
Если учащийся не может решить вопрос, он или она записывает правильный ответ. Если учащийся дает неверный ответ, он зачеркивает его и пишет правильный ответ.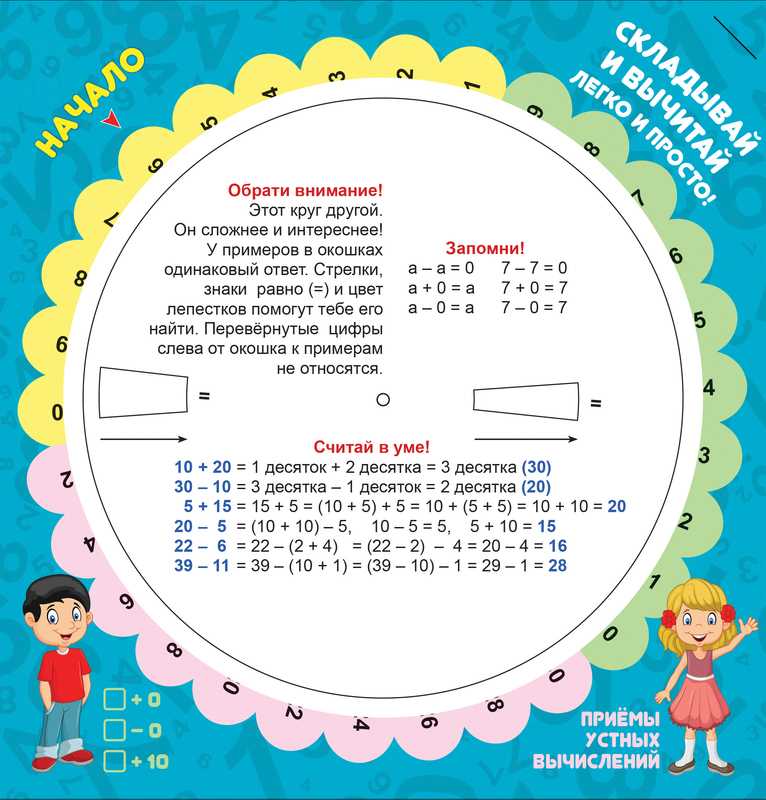
 Возьмите 18 x 5 в качестве примера задачи и попросите своих учеников решить ее в уме.
Возьмите 18 x 5 в качестве примера задачи и попросите своих учеников решить ее в уме.