Как делать наклоны: Наклоны вперед — как правильно делать, видео техники выполнения — AtletIQ.com

Содержание:

• Зачем тренировать поясницу?
• Какие мышцы в наклонах со штангой работают?
• Польза наклонов со штангой
• Техника наклонов со штангой
• Как делать наклоны со штангой правильно?
• Варианты наклонов
• Чем заменить наклоны со штангой?
• Заключение

Хит-парад мышц, качаемых в любом спортклубе, будет выглядеть так: бицепс, грудь, пресс.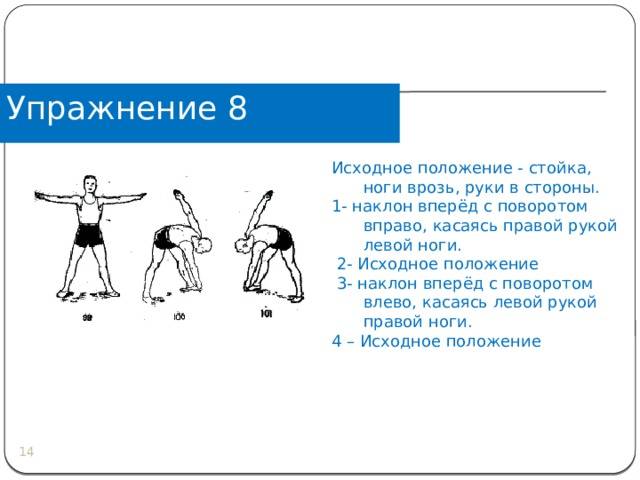 Именно на их развитие и уходит основная энергия большинства фанатов массонабора. До поясницы ли тут? Тем не менее, упражнения для низа спины обязательно должны присутствовать в арсенале всех, кто активно работает на массу. И не только их.

В наш век повальной сидячей работы, мышцы поясницы со временем приходят в совершенную негодность. Но стоит нам озаботится своим здоровьем и пойти в зал, как на поясничный отдел спины сразу ложится ощутимая нагрузка. Не только в приседаниях и тягах на спину, но и в жиме со штангой лежа, в сгибаниях с гантелями стоя и даже в упражнениях на пресс, поясница принимает активное участие.

Поэтому, появление сначала ломоты в нижнем отделе спины, а потом и хронической боли – лишь вопрос времени, особенно при чрезмерном увлечением прокачке мышц живота.  Та же планка – это отличное упражнение, но стояние в ней до посинения вызывает перенапряжение поясницы у большинства новичков.

Боль в пояснице у бодибилдера — это обычное дело

Но, как говорят спортивные врачи, причина этого не в травмах позвоночника или в ущемлении межпозвоночных дисков, все гораздо проще.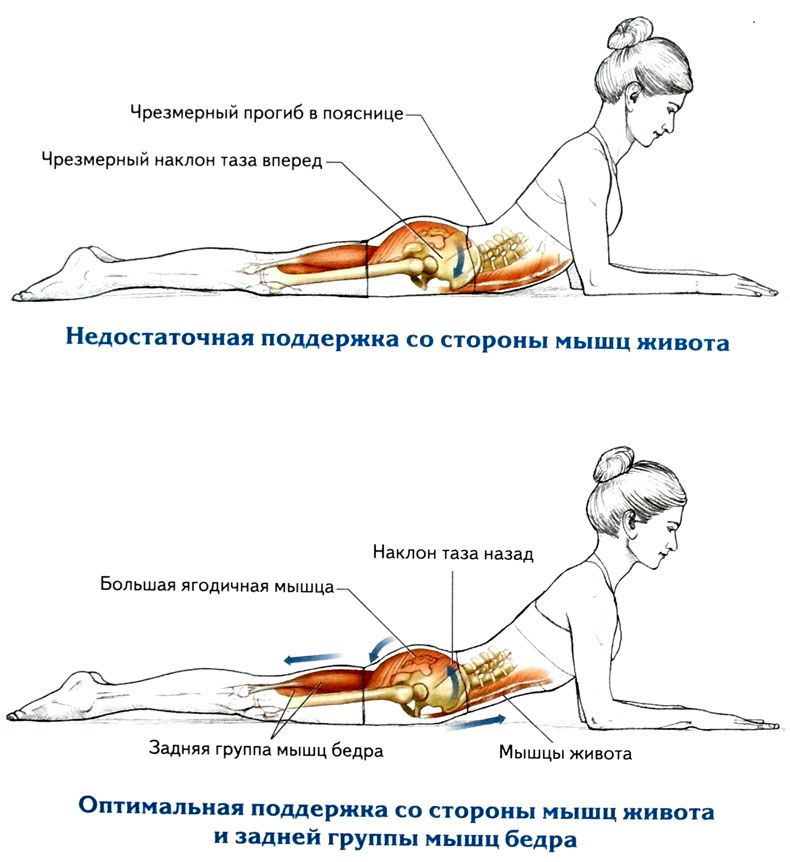 Это, так называемая спастическая судорога, которая возникает на фоне длительного статического напряжения пояснично-крестцового отдела спины во время выполнения различных упражнений. Чтобы избавиться от неё, нужно поясницу накачать, то есть сделать её банально сильнее. Уже после пары месяцев регулярной тренировки мышц поясницы, люди, не разгибавшиеся из-за постоянных болей в спине, начинают про них забывать.

Примечание: у меня всё было именно так, полюбив выполнять тягу гантели одной рукой, я довел вес снаряда до 75 кг. Только я её не спиной тянул, а рвал гантель с пола, забыв про всякую осторожность. В итоге, боль в пояснице, и превращение приседаний со штангой в настоящую пытку. После каждого подхода я искал место где можно присесть и опереться спиной, ибо стоять прямо было невыносимо. Но вот когда по совету бывшего штангиста, дяди Коли, я стал выполнять наклоны со штангой на плечах, боль ушла, приседать стало легче, веса пошли в гору, а ноги в рост.

Вывод: тренировать поясницу нужно обязательно. Наплевав на упражнения для этого отдела можно надолго выпасть из тренировочного процесса.

Уж не знаю кому пришло в голову назвать наклоны со штангой упражнением доброе утро (упражнение good morning), но движение действительно похоже на поклон — приветствие Солнцу, поэтому его так многие и называют.

Упражнение это старое, перекочевавшее в современные фитнес-центры (там, где его делают, конечно) прямо с тяжелоатлетических помостов. Все, кому важна сила и выносливость спины, регулярно включают его в свою тренировочную программу. В наклонах со штангой работают следующие мышцы:

• Разгибатели спины
• Ромбовидные мышцы
• Мышц шеи
• Мышцы поясницы
• Квадрицепсы
• Большая ягодичная мышца
• Бицепсы бедер
• Прямая и косая мышцы живота

Примечание: помимо целевых мышц, большая нагрузка ложится на подколенные сухожилия и связки, они становятся крепче. Это благотворно сказывается на результатах в таких упражнениях, как фронтальные приседания и выпады.

Вывод: в наклонах со штангой работают мышцы, так называемой, «задней цепи». Массу телу они не дают, но существенно помогают в развитии силового потенциала всего тела.

Польза наклонов со штангой очевидна, пускай не для каждого посетителя тренажерного зала, а в основном для опытных атлетов, понимающих зачем качать поясницу. Но, если свести воедино все плюсы от этого упражнения получится следующая картина:

• Улучшение осанки
• Укрепление разгибателей спины и мышц пояснично-крестцового отдела
• Повышение силовых показателей во всех без исключения базовых упражнениях
• Улучшение детализации и мускулистости спины
• Повышение плотности ягодичных мышц и бицепсов бёдер
• Профилактика травм позвоночника
• Восстановление в период реабилитации после перенесенных травм спины
• Активизация кровоснабжения в мышцах тазового дна и, как следствие, профилактика варикоза нижних конечностей
• Доступность и простота исполнения

Польза наклонов со штангой очень существенна

Вывод: упражнение good morning – это своеобразный предохранитель. Оно защищает от перегрузки низ спины и повышает отдачу от выполнения большинства упражнений.

Наклоны со штангой стоя — упражнение само по себе довольно простое, поскольку выполняется за счёт сгибания лишь одного сустава – тазобедренного, но все же имеет свои тонкости исполнения:

Шаг 1. Берём гриф от штанги и укладываем в район загривка, как раз в то место, где он лежит во время приседаний. Становимся прямо, ноги в коленях чуть сгибаем и расставляем их немного шире плеч. Напрягаем мышцы верха спины, сжимаем лопатки и делаем небольшой прогиб в пояснице, подав таз вперёд. Это стартовая позиция.

Шаг 2. Делаем вдох и, удерживая спину в напряжении, медленно наклоняемся вперёд. При этом прогиб в пояснице сохраняем, а ягодицы отводим назад. Наклоняемся до тех пор, пока корпус не станет почти параллелен полу. Выдыхаем и без задержки, исключительно за счёт усилий мышц разгибателей спины, возвращаемся в исходное положение.

Примечание: если наклонятся на согнутых ногах, основная часть нагрузки уйдёт на мышцы спины, а если ноги держать прямыми, в работу активно включатся ягодицы и бицепс бедра.

Вывод: сама техника наклонов со штангой довольно проста, согнулся-разогнулся. Сложность кроется в жестком контроле за поясницей на всем протяжение упражнения.

Это не упражнение для набора массы, у него, как и у кубинского жима, например, совершенно иные задачи. Делать наклоны со штангой стоя правильно совсем не сложно, но, тем не менее, есть ряд правил их выполнения:

• Не давать грифу скатываться вниз по спине. Он должен лежать строго на трапециях
• Не «клевать носом», смотреть вперёд
• Не округлять спину, пытаясь разглядеть себя в боковом зеркале
• Не спешить. Чем дольше длится фаза наклона, тем активнее работают целевые мышцы
• Не стоит начинать свой комплекс тренировки ног или спины с наклонов со штангой.
  Оптимальное время для них – завершение занятия.

Примечание: гнаться за ростом нагрузки в этом упражнении для низа спины не стоит. Идеальный вес штанги в этом упражнении – 20-25% от величины рабочего веса в приседаниях. Объём – 3 подхода по 8-10 повторений в каждом. Периодичность – 1-2 раза в неделю.

Вывод: упражнение доброе утро — это профилактика, а не работа до отказа. Задача – предотвратить появление травм, а не заработать новые.

Разновидностей этого упражнения существует немного, но, при желании, освежить и модифицировать можно даже и его.

Смысл такой «одноногой» версии заключается в том, что таким образом, как и в любом ином унилатеральном упражнении, можно сместить нагрузку на одну из сторон тела.

Наклоны со штангой на плечах стоя на одной ноге

Наклоны со штангой стоя на одной ноге – упражнение специфическое и узкопрофессиональное. Его обычно используют атлеты, остро нуждающиеся в повышении силовых показателей подколенных связок и сухожилий. В этом плане таким наклонам равных нет.

А вот так качать поясницу предпочитаю силовики, ибо в положении сидя на скамье, мышцы ног и ягодиц из работы исключаются, зато нагрузка на разгибатели спины и на мышцы поясницы возрастает в разы.

Наклоны сидя со штангой

Устойчивое положение тела позволяет, по сравнению с обычной версией упражнения, использовать штангу большего веса. Поэтому, наклоны со штангой сидя на скамье пользуются популярностью у атлетов, стремящихся быстро повысить силовой потенциал спины. Правда, такой способ тренировки поясницы является одним из наиболее травмоопасных

Самая изолированная разновидность наклонов со штангой, ибо стабилизация тела обеспечивается самой конструкцией моего любимого тренажера. Выполняют наклоны со штангой на плечах в Смите в двух вариантах: стоя на полной стопе и стоя на пятках. Но обе версии упражнения служат для решения одной и той же задачи – максимальной растяжки ягодичных мышц и задней поверхности бедра.

Упражнение носит формирующий характер и используется в основном, представительницами прекрасной половины тренажёрных залов для придания жёсткости и проработанности мышцам «задней цепи».

Вывод: вариантов наклонов со штангой немного, но каждый из них имеет свои особенности и служит для решения конкретной задачи.

Несмотря на простоту и эффективность этого упражнения для низа спины, далеко не каждому по душе его выполнять. Тем более, что оно имеет несколько превосходных аналогов, решающих задачу тренировки мышц поясницы ничуть не хуже. Поэтому, заменить наклоны со штангой стоя можно вот этими упражнениями:

Почему румынская, а не становая? Объясняю, румынскую тягу придумал атлет сначала румынской, потом австралийской олимпийской сборной по тяжелой атлетике Нику Влад. И если становая тяга служит для набора массы всего тела, то это упражнение было изначально придумано именно для прокачки разгибателей спины и поясницы.

Румынская тяга со штангой.

Все его отличие от становой тяги заключается в том, что штанга на пол не опускается, а зависает в нижней точке на уровне середины голеней. Нет смысла даже сравнивать наклоны со штангой и румынскую тягу по величине рабочего веса. Произведение Нику Влада даст им 100 очков по эффективности, но в техническом плане оно в разы сложнее.

Гиперэкстенизия – это лайт-версия наклонов стоя, поскольку выполняется в специальном тренажере и позволяет тренировать мышцы спины при жестко закреплённом корпусе. Для тех, кто пришел в зал просто за здоровьем, а не за массой, это готовый ответ на вопрос, как накачать поясницу.

Гиперэкстензия в тренажере

Удобное, понятное, легкое. Правда, у этого упражнения есть сестра, обратная гипреэкстензия. Ее автор — Луи Симмонс, легендарный Левиафан силы. Получив тяжелейшую травму поясницы, но при этом и не думая бросать силовой спорт, он и придумал такой способ тренировки низа спины. Не удивительно, что оно занимает почетное место в арсенале всех пауэрлифтеров.

Примечание: Луи Симмонс помимо обратной гиперэкстензии придумал ещё и калифорнийский жим— любимое упражнение для трицепса самого Арнольда Шварценеггера.

Вот, кто придумал такую оригинальную версию наклонов, я не скажу. Это упражнение также имеет право на существование, правда отдача от него, по сравнению с предыдущими движениями, существенно ниже.

Наклоны на нижнем блоке с веревочной рукоятью

Нагрузка на разгибатели спины в нем минимальная, а львиная часть работы по разгибанию корпуса, выполняется за счет поясничных мышц. Идеально подходит для реабилитации после перенесенной травмы.

Вывод: заменить наклоны со штангой при желании можно легко, главное, определиться, для какой цели то или иное упражнение для поясницы должно служить.

Заключение

Надеюсь, моя статья про тренировку поясницы окажется полезной, и позволит наклонам со штангой либо ее аналогам прочно обосноваться в вашем арсенале упражнений. Да пребудет с вами сила. И масса!

Об авторе: Меня зовут Станислав Михайловский. Я автор этого блога, персональный тренер по бодибилдингу, диетолог, специалист по спортивному питанию, писатель. Мне 46 лет, из них почти 30, занимаюсь силовым тренингом.

Разрабатываю индивидуальные тренировочные программы для набора массы и похудения, составляю рационы, консультирую по выбору и использованию спортивных добавок. Специализация – бодибилдинг после 40.

Как использовать формулу наклона и найти наклон линии, независимо от того, является ли наклон положительным, отрицательным или неопределенным.

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)

Наклон линии характеризует направление линии. Чтобы найти наклон, вы делите разницу координат y двух точек на прямой на разницу координат x тех же двух точек.

Разные слова, та же формула

Учителя используют разные слова для координат y и координат x.

1. Некоторые называют координаты у подъемом, а координатами х — бег.
2. Другие предпочитают использовать нотацию $$\Delta$$ и называть y-координаты $$\Delta y$$ , а x-координаты $$\Delta x$$ .

Все эти слова означают одно и то же , то есть значения y находятся вверху формулы (числитель), а значения x внизу формулы (знаменатель)!

Пример 1

Наклон линии , проходящей через точку (1, 2) и точку (4, 3), равен $$ \frac{1}{3}$$.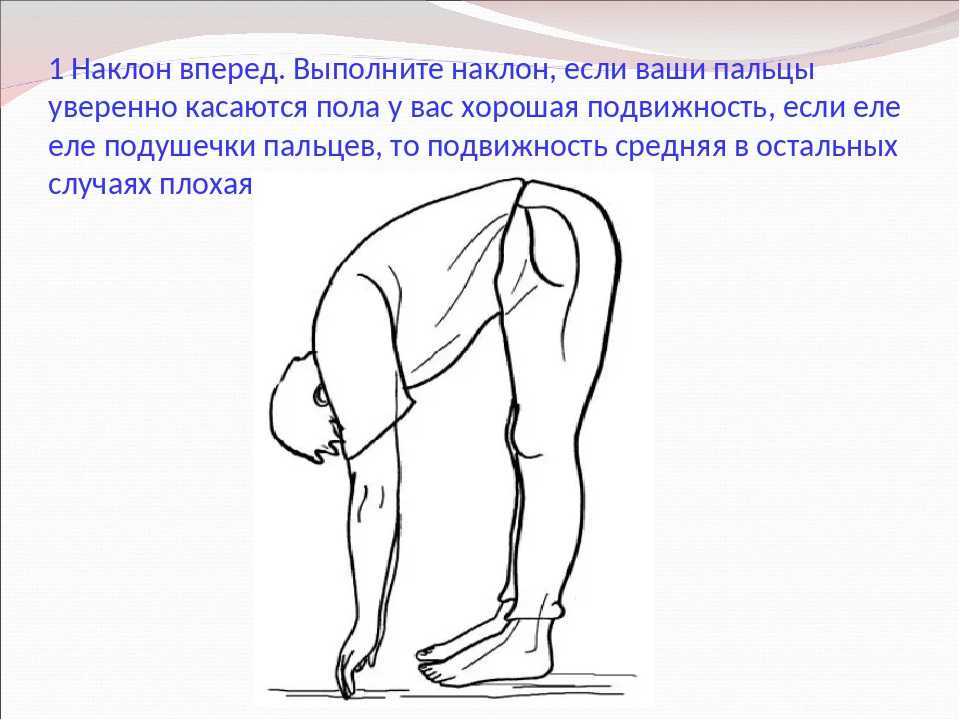

Помните: разница в значениях y идет в числителе формулы, а разница в значениях x идет в знаменателе формулы.

Может ли любая из точек быть $$( x_1 , y_1 ) $$ ?

Есть только один способ узнать!

Во-первых, мы будем использовать точку (1, 2) как $$x_1, y_1$$, и, как вы можете видеть: наклон: $ \boxed {\frac{1}{3} }$ .

Теперь давайте используем точку (4, 3) как $$x_1, y_1$$, и, как вы можете видеть, наклон упрощается до того же значения: $ \boxed {\frac{1}{3} }$ .

Работа рядом

точка (4, 3) как $$ (x_1, y_1 )$$

Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$

точек (1, 2) как $$ (x_1, y_1 )$$

Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{- 3} = \frac{1}{3} $$

Ответ: , а не не имеет значения, какую точку поставить первой. Вы можете начать с (4, 3) или с (1, 2), и в любом случае вы закончите точно таким же числом! $$ \фракция{1}{3} $$

Пример 2 наклона линии А

Наклон линии , проходящей через точки (3, 4) и (5, 1), равен $$- \frac{3}{2}$$, потому что каждый раз, когда линия опускается на 3 (изменение y или подъем) линия смещается вправо (разбег) на 2.

Эта страница:

• Формула
• Пример
• Видео
• Заказать?
• Любые две точки определяют наклон линии?
• Наклон вертикальной линии
• Наклон горизонтальной линии
• Практические задачи

Наклон вертикальных и горизонтальных линий

Наклон вертикальной линии не определен

Это связано с тем, что любая вертикальная линия имеет $$\Delta x$$ или «пробег» нуля. Всякий раз, когда ноль является знаменателем дроби в этом случае дроби, представляющей наклон линии, дробь не определена. На рисунке ниже показана вертикальная линия (x = 1).

Наклон горизонтальной линии равен нулю

Это потому, что любая горизонтальная линия имеет $$\Delta y$$ или «подъем» нуля. Следовательно, независимо от того, каков пробег (при условии, что он не равен нулю!), дробь, представляющая уклон, имеет в числителе ноль. Следовательно, наклон должен оцениваться как нулевой. Ниже приведено изображение горизонтальной линии — вы можете видеть, что у нее нет «подъема».

Любые две точки на прямой имеют одинаковый наклон?

Ответ: Да, и это фундаментальный момент, который следует помнить при расчете уклона.

Каждая линия имеет постоянный наклон. Другими словами, наклон линии никогда не меняется. Эта фундаментальная идея означает, что вы можете выбрать 90 123 любых 90 124 2 точек на линии.

Подумайте об идее прямой линии. Если бы наклон линии изменился, то это была бы зигзагообразная линия, а не прямая линия, как вы можете видеть на рисунке выше.

Как вы можете видеть ниже, наклон одинаков независимо от того, какие 2 точки вы выбрали.

Наклон линии

Эта страница:

• Формула
• Пример
• Видео
• Заказать?
• Любые две точки определяют наклон линии?
• Наклон вертикальной линии
• Наклон горизонтальной линии
• Практические задачи

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)

Проблема 1

Каков наклон прямой, проходящей через точки (10,3) и (7, 9)?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

Используя $$ \red{ (10,3)}$$ как $$x_1, y_1$$

$ \frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3} \\ = \ в коробке {-2 } $

Используя $$ \red{ (7,9)} $$ как $$x_1, y_1$$

$ \frac{3- \red 9{10- \красное 7} \\ =\ гидроразрыв{-6}{3} \\ = \в коробке{-2} $

Проблема 2

Прямая проходит через (4, -2) и (4, 3). Каков его наклон?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

Используя $$ \red{ ( 4,3 )}$$ как $$x_1, y_1$$

$ = \frac{-2 — \red 3}{4- \red 4} «=» \frac{-5}{\color{red}{0}} \\ = \text{неопределенный} $

Используя $$ \red{ ( 4, -2 )}$$ как $$x_1, y_1$$

$ = \frac{3- \red{-2}}{4- \red 4} «=» \frac{5}{\color{red}{0}} \\ = \текст{неопределенный} $

Всякий раз, когда длина линии равна нулю, наклон не определен. Это потому, что в знаменателе наклона стоит ноль! Любой наклон любой вертикальной линии не определен.

Проблема 3

Прямая проходит через (2, 10) и (8, 7).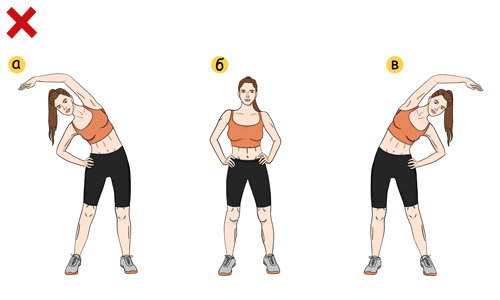 Каков его наклон?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

Используя $$ \red{ ( 8, 7 )}$$ как $$x_1, y_1$$

$ \frac{10 — \red 7}{2 — \red 8} \\ = \ гидроразрыва {3}{-6} \\ = -\фракция{1}{2} $

Используя $$ \red{ ( 2,10 )}$$ как $$x_1, y_1$$

$ \frac{7 — \red {10}}{8- \red 2} \\ = \ гидроразрыв {-3} {6} \\ = -\фракция{1}{2} $

Проблема 4

Прямая проходит через (7, 3) и (8, 5). Каков его наклон?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

Используя $$ \red{ (7,3 )}$$ как $$x_1, y_1$$

$$ \frac{ 5- \red 3}{8- \red 7} \\ = \ гидроразрыва {2} {1} \\ = 2 $$

Используя $$ \red{ ( 8,5 )}$$ как $$x_1, y_1$$

$$ \frac{ 3- \red 5}{7- \red 8} \\= \фракция{-2}{-1} \\ = 2 $$

Проблема 5

Прямая проходит через (12, 11) и (9, 5) . Каков его наклон?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

Используя $$ \red{ ( 5, 9)}$$ как $$x_1, y_1$$

$$ \frac{ 11 — \red 5}{12- \red 9} \\ = \ гидроразрыва {6} {3} \\ =2 $$

Используя $$ \red{ (12, 11 )}$$ как $$x_1, y_1$$

$$ \frac{ 5- \red{ 11} }{9- \red { 12}} \\ = \фракция{-6}{-3} \\ = 2$$

Проблема 6

Каков наклон линии, проходящей через (4, 2) и (4, 5)?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

Используя $$ \red{ ( 4,5 )}$$ как $$x_1, y_1$$

$$ \frac{ 2 — \red 5}{4- \red 4} \\ = \frac{-3}{\color{red}{0}} \\ = не определено $$

Используя $$ \red{ ( 4,2 )}$$ как $$x_1, y_1$$

$$ \frac{ 5 — \red 2}{4- \red 4} \\ = \frac{ 3}{\color{red}{0}} \\ = не определено $$

ПРЕДУПРЕЖДЕНИЕ! Сможете ли вы уловить ошибку в следующей задаче: Дженнифер пыталась найти наклон, проходящий через точки $$(\color{blue}{1},\color{red}{3})$$ и $$ (\color {синий}{2}, \цвет{красный}{6})$$ .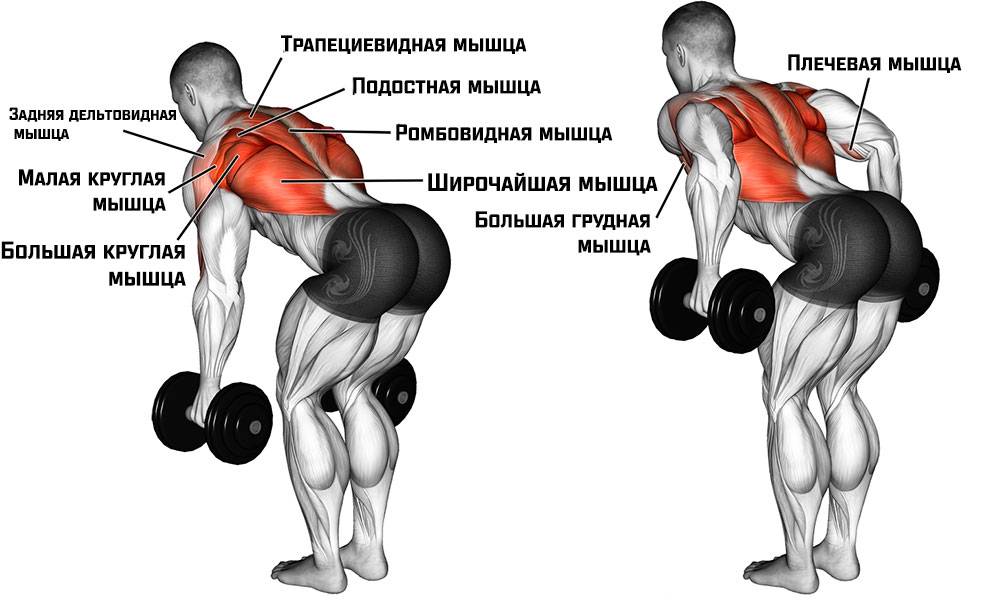 У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза и дала 3 разных ответа. Сможете ли вы определить правильный ответ?

Задача-вызов

Найдите наклон прямой через две точки.

Попытка №1

$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} «=» \ гидроразрыв {6-3} {1-2} \\= \фракция{3}{-1} =\в коробке{-3} $

Попытка #2

$$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} «=» \фракция{6-3}{2-1} \\= \фракция{3}{1} \\ = \в коробке{3} $$

Попытка №3

$$ уклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} \\ =\ гидроразрыва {2-1} {6-3} \\ =\в коробке{ \frac{1}{3}} $$

Правильный ответ — попытка №2.

В попытке №1 она не всегда использовала очки. В первой попытке она сделала следующее:

$$ \frac{\color{red}{y{\boxed{_2}}-y_{1}}}{\color{blue}{x\boxed{_{1}}-x_{2}}} $$

Проблема с попыткой №3 заключалась в обратном подъеме и беге. Она поместила значения x в числитель (сверху), а значения y в знаменатель, что, конечно же, противоположно!

$$ \ отмена {\ frac {\ color {синий} {x_ {2} -x_ {1}}} {\ color {red} {y_ {2} -y_ {1}}}} $$

Вы можете сколько угодно практиковаться в решении подобных задач с помощью приведенного ниже генератора задач на уклон.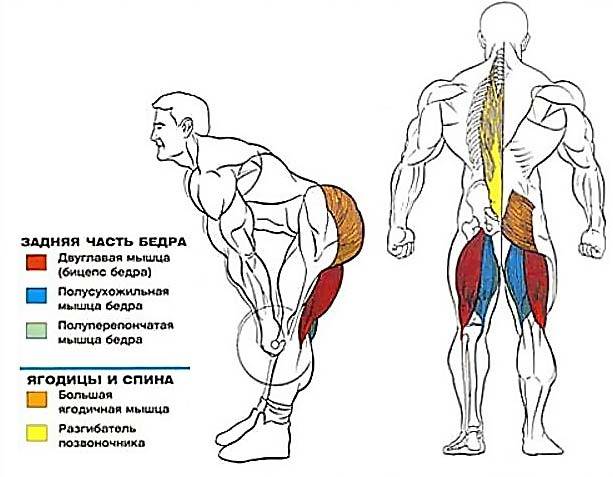

Он будет случайным образом генерировать числа и запрашивать наклон линии через эти две точки. Вы можете выбрать, насколько большими будут числа, регулируя уровень сложности.

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)

Algebra 1 Help

Студенты, нуждающиеся в помощи по алгебре 1, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Алгебре 1. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы мгновенно получите много помощи по Алгебре 1. Получите помощь сегодня с нашей обширной коллекцией необходимой информации по алгебре 1.

• Алгебра 1

• Распределительная собственность

• Как использовать FOIL в дистрибутивной собственности

• Как использовать метод сетки для FOIL

• Уравнения / Неравенства

• Системы уравнений

• Уравнения/наборы решений

• Как разложить уравнение на множители

• Как найти решение set

• Как найти решение системы уравнений

• Линейные/рациональные уравнения/уравнения с переменными

• Как узнать, когда уравнение не имеет решения

• Как найти решение рационального уравнения с LCD

• Как найти решение уравнения

• Квадратные уравнения

• Как разложить квадратное уравнение на множители

• Как найти решение квадратного уравнения

• Системы неравенств

• Как найти решение неравенства со сложением

• Как найти решение неравенства с делением

• Как найти решение неравенства с умножением

• Как найти решение неравенства с вычитанием

• Функции и линии

• Алгебраические функции

• Как найти прямой вариант

• Как найти f(x)

• Как найти обратную вариацию

• Как найти домен функции

• Как использовать квадратичную функцию

• Уравнения прямых

• Формула средней точки

• Как найти концы отрезка

• Как найти середину отрезка

• Параллельные линии

• Как узнать, параллельны ли прямые

• Как найти уравнение параллельной прямой

• Как найти наклон параллельных прямых

• Перпендикулярные линии

• Как узнать, перпендикулярны ли прямые

• Как найти уравнение перпендикулярной прямой

• Как найти наклон перпендикулярных линий

• Точки и формула расстояния

• Как узнать, находится ли точка на прямой с уравнением

• Как найти длину линии по формуле расстояния

• Уравнения наклона и линии

• Как найти наклон линии

• Как найти уравнение прямой

• Графика

• Как построить график функции

• Как построить линию

• Как нарисовать точку

• Как построить график квадратичной функции

• Как построить график двухшагового неравенства

• Как построить график функции абсолютного значения

• Как построить график экспоненциальной функции

• Как построить график упорядоченной пары

• последовательности

• Как найти последовательные целые числа

• Как найти ответ на арифметическую прогрессию

• Как найти общее различие в последовательностях

• Как найти следующий член арифметической прогрессии

• Как найти n-й член арифметической прогрессии

• Линейные уравнения

• Преобразование измерений

• Как решать уравнения абсолютного значения

• Как решить одношаговые уравнения

• Как решать двухшаговые уравнения

• Как писать выражения и уравнения

• Проценты

• Пропорции

• Линейные неравенства

• Неравенства абсолютного значения

• Графические неравенства

• Запись неравенств

• Проценты

• Десятичные числа и проценты

• Как найти десятичный эквивалент процента

• Как найти процент, эквивалентный десятичной дроби

• Дроби и проценты

• Как найти дробь от процента

• Как найти дробные проценты

• Как найти процент от дроби

• Денежный процент

• Как найти размер прибыли

• Как найти простые проценты

• Как найти сумму налога с продаж

• Как узнать цену продажи

• Процент изменения

• Как найти процент уменьшения

• Как найти процент увеличения

• Целиком и частично

• Как найти часть от целого в процентах

• Как найти целое из части с процентами

• Реальные числа

• Подсчет/наборы

• Как найти недостающее число в наборе

• Как найти количество целых чисел между двумя другими целыми числами

• Целочисленные операции

• Как складывать целые числа

• Как делить целые числа

• Как умножать целые числа

• Как вычитать целые числа

• Количество линий и абсолютное значение

• Как найти абсолютное значение

• Как найти значение с числовой строкой

• Как построить график неравенства с числовой прямой

• Как построить дроби на числовой прямой

• Статистика и вероятность

• Как найти межквартильный размах

• Как найти среднее

• Как найти медиану

• Как найти режим

• Как найти диапазон

• Как найти стандартное отклонение

• Переменные

• мономы

• Как делить одночленные частные

• Как умножить одночлен на многочлен

• Как умножать одночленные частные

• Многочлены

• Биномы

• Как найти решение рационального уравнения с биномиальным знаменателем

• Как найти решение биномиальной задачи

• Как найти значение коэффициента

• Как умножать биномы с распределительным свойством

• Как упростить биномы

• Факторные полиномы

• Как разложить многочлен на множители

• Как факторизовать переменную

• Полиномиальные операции

• Как складывать полиномы

• Как делить многочлены

• Как найти степень многочлена

• Как умножать многочлены

• Как вычитать многочлены

• Трехчлены

• Как складывать трехчлены

• Как делить трехчлены

• Как разложить трехчлен на множители

• Как умножать трехчлены

• Как вычитать трехчлены

Алгебра I часто впервые знакомит учащихся с процессами вычисления переменных, понимания неравенств и использования порядка операций для упрощения выражений.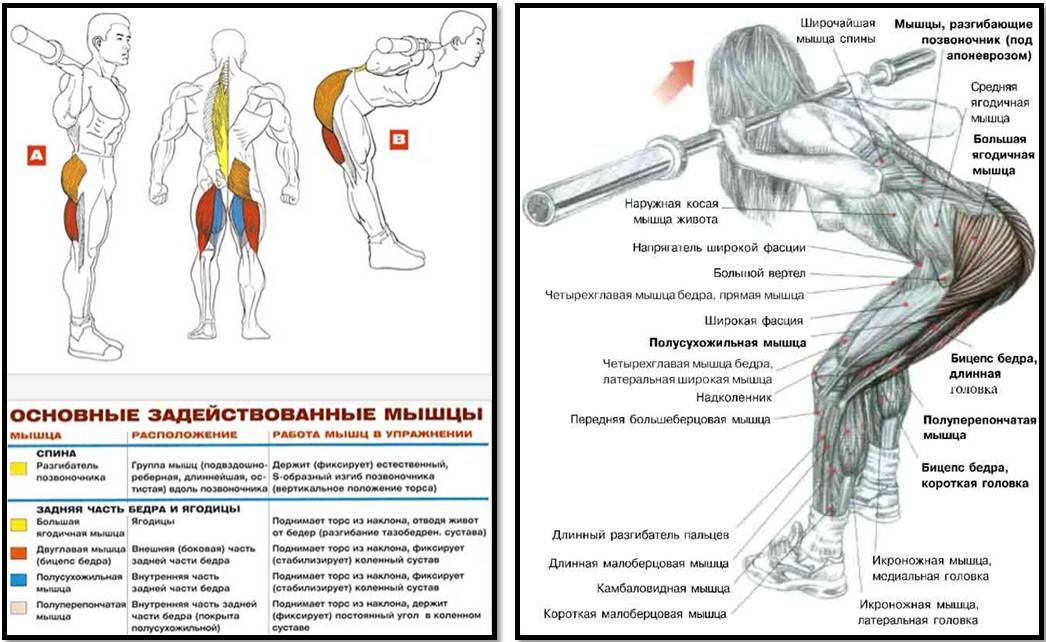 Некоторым учащимся часто бывает трудно освоить эти новые навыки; однако усердная практика основных алгебраических принципов жизненно важна для успеха в дальнейших курсах математики. Понимание геометрии, предварительного исчисления, исчисления и высшей математики, физики и химии требует фундаментального понимания того, как упростить выражения и манипулировать переменными. Нужны ли вам лучшие репетиторы по алгебре 1 в Бостоне, репетиторы по алгебре 1 в Детройте или лучшие репетиторы по алгебре 1 в Далласе, Форт-Уэрт, работа с профессионалом может вывести ваше обучение на новый уровень.

В общем, Алгебра I фокусируется на основах понимания и упрощения задач. Учащиеся работают над тем, чтобы логически продумать этапы решения проблемы, не делая немедленных выводов или решений. Кроме того, учащихся учат объяснять отношения между уравнениями, давать словесные описания графиков, таблиц и диаграмм и предсказывать форму фигур на основе математических соотношений. Репетиторы Varsity Tutors предлагают такие ресурсы, как бесплатные практические тесты по алгебре 1, которые помогут вам в самостоятельном обучении, или вы можете подумать о репетиторах по алгебре 1.

Общие темы по алгебре I включают:

• Арифметика с полиномиальными и рациональными выражениями: учащимся предлагается упростить числовые выражения с помощью порядка операций, разложить переменные в числовые уравнения и упростить сложные выражения с различными комбинациями чисел и переменных.

• Создание выражений: используя графики и таблицы в качестве ориентира, учащимся предлагается определить взаимосвязь между двумя или более переменными. Например, учащимся может быть предоставлена ​​таблица пройденного расстояния и времени, необходимого для преодоления этого расстояния. Ожидается, что учащиеся определят, как пройденное расстояние влияет на затраченное время (удвоение пройденного расстояния требует удвоения времени при той же скорости).

• Рассуждения с помощью уравнений и неравенств: учащиеся, изучающие алгебру I, должны найти значение переменных, упрощая числовые выражения. Кроме того, студентов учат, как графически отображать эти решения в системах координатной плоскости. Также рассматриваются неравенства и определение того, как будет затеняться график системы координат на основе численного решения.

• Видение структуры в выражении: использование рассуждений с уравнениями и неравенствами в качестве основы, учащихся учат писать алгебраические выражения и неравенства на основе графиков, а иногда и таблиц данных.

Ключом к успеху в алгебре I является постоянная практика. В то время как некоторые учащиеся будут иметь опыт упрощения выражений, добавление графиков, диаграмм, неравенств и факторизации будет новым для других. Общие стратегии достижения успеха включают просмотр кратких резюме в учебниках перед выполнением домашних заданий и отработку дополнительных 10–15 заданий после выполнения назначенных отрывков домашнего задания. Часто учащиеся изучают шаблоны, необходимые для решения задач, путем постоянного повторения вместо того, чтобы читать разделы книги.