Формула эллипсоида: Недопустимое название — Циклопедия

Тема №1 основные формулы и соотношения на поверхности земного эллипсоида

9

1. Основные параметры земного эллипсоида и соотношения между ними.

Математически определяемой фигурой, наилучшим образом представляющей собой тело Земли в целом, является эллипсоид вращения. На рис. 1.1 изображен эллипсоид вращения, полученный путем вращения эллипса РЕ₁Р₁Е вокруг линии РР₁ ,как вокруг оси (иногда эллипсоид вращения называют сфероидом).

Рис. 1.1

Размеры эллипсоида вращения определяются следующими величинами:

а = ОЕ = OE₁ =ОА — большая полуось эллипсоида;

b=ОР = ОР₁ — малая полуось эллипсоида;

α = —полярное сжатие эллипсоида, которое определяется соотношением:

e — первый эксцентриситет меридианного эллипса, определяемый по формуле:

; (1.2)

e΄ — второй эксцентриситет меридианного эллипса, определяемый по формуле:

; (1.3)

Параметры а, b, α, e, e΄ являются основными, определяющими эллипсоид вращения, однако для определения эллипсоида вращения достаточно знать только два из них (один обязательно линейный).

Между перечисленными основными параметрами земного эллипсоида, кроме соотношений (1.1), (1.2) и (1.3) существуют еще следующие зависимости:

а).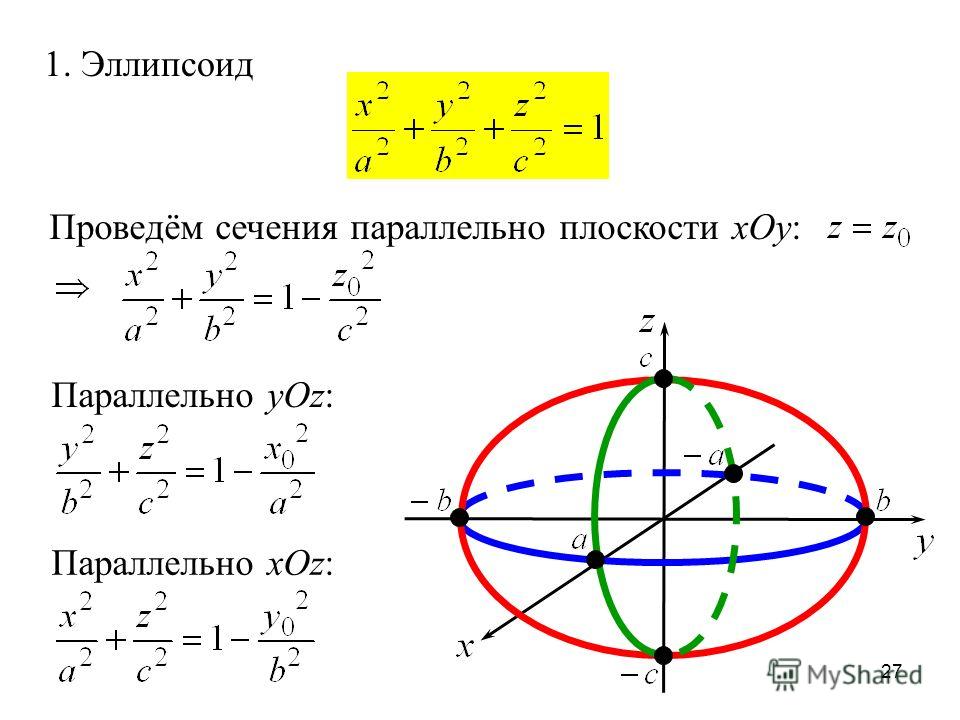 Между e и e΄

. (1.4)

Согласно (1.3) ,

откуда

,

и окончательно

. (1.5)

Аналогичные преобразования дадут:

. (1.6)

а). Между e и α

Из формулы (1.4) следует, что

, (1. 7)

но по (1.1) имеем:

;

или с учетом (1.7)

(1.8)

Из (1.8) имеем:

,

откуда

, (1.9)

или приближенно

. (1.10)

Для эллипсоида Красовского эти основные элементы имеют следующие числовые значения:

a = 6 378 245,00000 м lga = 6.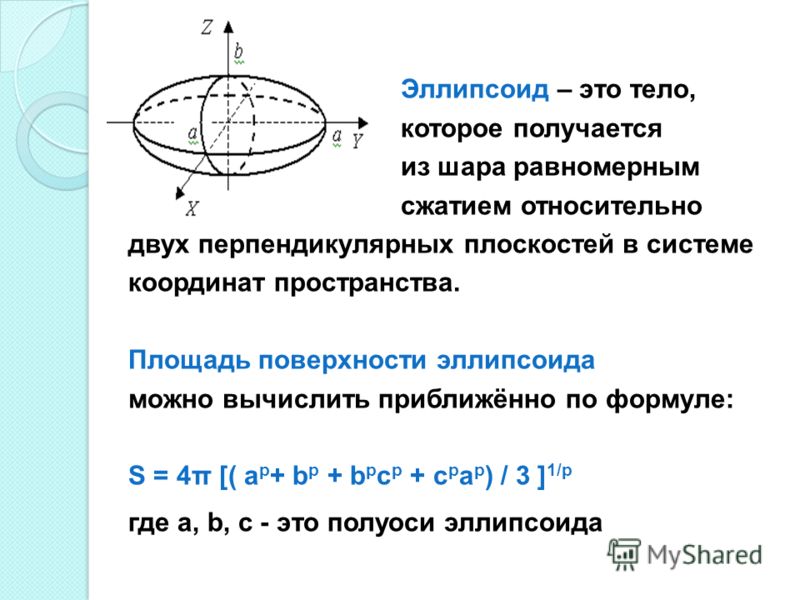 804 60119 73

b = 6 356 863,01877 м lgb = 6.803 24285 31

c = 6 399 698,90178 м lgc = 6.806 15954 14

α = 0,003 35232,9869 lgα

e² = 0,006 69342,1623 lg e²= 7.825 6481823^-10

e’²=0,006 73852 5415 lg e’²=7.828 5648706^-10

Аналитическая геометрия

Если растянуть координату $y$, то мы получим уравнение общего эллипсоида \begin{equation} \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1. 2+12xy+8yz+12x+4y+8z-1=0$.

&nbsp

5.1 Поверхности вращения

&nbsp

Калькулятор объема эллипсоида

Создано Луцией Заборовской, доктором медицинских наук, кандидатом наук

Отзыв Стивена Вудинга

Последнее обновление: 23 ноября 2022 г. ?

Вам нужен калькулятор объема эллипсоида? Вы только что нашли идеальное место! Мы собираемся вычислить объем эллипсоида и дадим вам пошаговое решение, чтобы вы могли научиться делать это самостоятельно .

Следуйте приведенной ниже статье и узнайте о формуле объема эллипсоида , свойствах формы эллипсоида и другой полезной информации.

Эллипсоид — полезная форма

Эллипсоид — это поверхность, которую можно получить, «сжав» обычный шар. Он похож на мяч для американского футбола со сглаженными углами. 🏈 Что интересно, все сечения эллипсоида имеют форму эллипса .

Определяем эллипсоиды с помощью полуосей — отрезков, которые начинаются в самом центре эллипсоида и заканчиваются в точке касательной к поверхности (вы можете думать об этом так же, как вы сделать о радиусе круга ). Мы можем различать три типа полуосей:

На основании поперечного сечения эллипсоида (эллипса):

• Большая полуось — самая большая; и
• Малая полуось — ось под прямым углом к большой полуоси.

3D модификация:

• Третья ось расположена под прямым углом к ​​ двум последующим осям .

Все три полуоси сходятся в центре эллипсоида

Зачем нужен объем эллипсоида? 🤔 Эта форма довольно распространена в природа . Обычно используется в медицине для оценки объема различных органов, таких как:

• Яичники;
• Простата; или
• Мочевой пузырь.

Сам эллипс также используется при расчете движения планет (см. наш калькулятор орбитальной скорости).

Как пользоваться калькулятором эллипсоида?

Наш калькулятор объема эллипсоида прост в использовании и состоит из двух основных шагов:

1. Найдите длины всех трех осей эллипсоида.

   Все они должны находиться под углом 90° ( под прямым углом ) друг к другу.

2. Введите полученные значения и наслаждайтесь результатом! 🎉

Мы покажем формулу объема эллипсоида, а также наше решение — во всех возможных единицах, которые только пожелает ваше сердце!

Вы готовы идти? Вы также можете попробовать наши all-shapes калькулятор объема или калькулятор объема сферы. 🌎

Как рассчитать объем эллипсоида?

Мы можем вычислить объем эллиптической сферы с помощью простого и элегантного уравнения эллипсоида:

Объем = 4/3 * π * A * B * C ,

где:

• A

  2 , 1 B

  2 и C — длины всех трех полуосей эллипсоида.

Формула эллипсоида

В этом разделе показано, как можно обозначить эллипсоид двумя разными способами.

Нам нужно использовать декартову систему координат в трех измерениях (x, y, z). Затем нам нужно установить начало системы координат (0, 0, 0) как центр эллипсоида .

1. Использовать значения полуосей

   Найдите эти три точки в системе координат:

   • (А, 0, 0)
   • (0, Б, 0)
   • (0, 0, С)

   Это точки поверхности, которые составляют границу вашего эллипсоида.

2. Используйте формулу эллипсоида

   1 = (x²/A²) + (y²/B²) + (z²/C²)

   Это уравнение также полезно, если вам нужно найти значение любой из полуосей.

Реальные приложения

В беспроводной связи у нас есть трехмерная эллиптическая область (объем эллипсоида) между антенной передатчика и антенной приемника . Эта область определяется расстоянием между антеннами и частотой беспроводной волны. Это называется Зона Френеля и выглядит так:

Основной объем эллипсоида, называемый зоной Френеля, должен оставаться свободным для обеспечения надлежащей беспроводной связи. Формулы для определения свободного пространства выводятся из основного уравнения эллипсоида, как описано здесь.

Люция Заборовска, доктор медицинских наук, кандидат наук

Полуось A

Полуось B

Полуось C

Объем

Проверить 21 похожий калькулятор 3d геометрии

Площадь полушарияCubeCube Рассчитать: найти v, a, d… еще 18

Объем эллипсоида — Веб-формулы

· Объем конуса
· Объем эллипсоида
· Объем сферы
· Объем цилиндра
· Объем прямоугольного параллелепипеда

· Периметр квадрата
· Периметр прямоугольника
· Периметр многоугольника
· Периметр параллелограмма
· Периметр круга
· Площадь квадрата
· Площадь прямоугольника
· Площадь многоугольника
· Площадь треугольника
· Площадь параллелограмма

Текущее местоположение   >  Математические формулы > Геометрия > Объем эллипсоида

Точно так же, как круг превращается в сплошную сферу, эллипс может стать сплошным «эллипсоидом».
Существует два особых типа эллипсоидов.

Предположим, у нас есть сфера, и мы растягиваем ее, чтобы сделать ее более длинной и тонкой (немного похожей на мяч для регби или дыню). В таком случае он называется вытянутым эллипсоидом. Если мы разрежем его пополам, чтобы получить круг, то объем равен площади круга, умноженной на 2/3 большой оси. (Большая ось — это максимальная длина от одного конца до другого.)

Однако, если у нас есть сфера, и мы сжимаем ее, чтобы сделать более короткую и толстую форму (немного похожую на гамбургер). В таком случае он называется сплюснутым эллипсоидом. Если мы разрежем его посередине, чтобы получить круг, то объем равен площади круга, умноженной на 2/3 малой оси.

Пример 1: Эллипсоид, радиус и оси которого равны a = 21 см, b = 15 см и c = 2 см соответственно. Определить объем данного эллипсоида.
Решение:
Volume of ellipsoid:

Пример 2: .