Эллипсоид и сфера
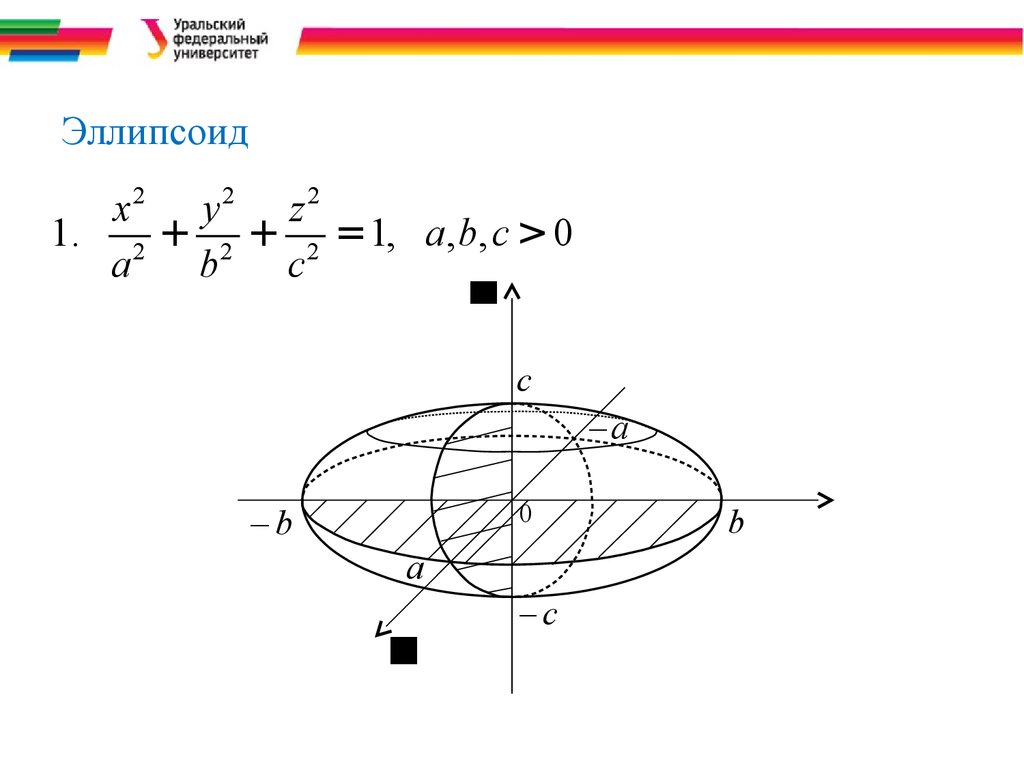
Каноническое уравнение эллипсоида имеет вид , где – положительные числа (полуоси эллипсоида), которые в общем случае различны. Эллипсоидом называют как поверхность, так и тело, ограниченное данной поверхностью. Тело задаётся неравенством и координаты любой внутренней точки (а также любой точки поверхности) обязательно удовлетворяют этому неравенству. Конструкция симметрична относительно координатных осей и координатных плоскостей:
Происхождение термина «эллипсоид» тоже очевидно: если поверхность «разрезать» координатными плоскостями, то в сечениях получатся три различных (в общем случае) эллипса. В зависимости от значений эллипсоид может быть вытянут вдоль любой оси, причём вытянут достаточно далеко.
Если две полуоси совпадают, то данную поверхность / тело называют эллипсоидом вращения. Так, например, эллипсоид получен вращением эллипса вокруг оси 
Небольшая задачка для самостоятельного решения:
Задача 173
Построить эллипсоид . Записать уравнение порождающего эллипса и ось, вокруг которой осуществляется его вращение.
Чертеж с комментариями в конце книги.
В случае равенства всех полуосей , эллипсоид вырождается в сферу:
– данное уравнение задаёт сферу с центром в начале координат радиуса .
Тело, ограниченное сферой, называется шаром. Неравенство определяет шар с центром в начале координат радиуса . И, соответственно, противоположному условию удовлетворяют координаты любой внешней точки.
Разделаемся с аппетитным Колобком:
Задача 174
Построить поверхность . Найти функции, задающие верхнюю и нижнюю полусферу, указать их области определения. Записать аналитическое выражение шара, ограниченного данной сферой и проверить, принадлежат ли ему точки .
Решение: уравнение задаёт сферу с центром в начале координат радиуса 2. Здесь, как и в примерах с параболическими цилиндрами, удобно уменьшить масштаб чертежа:
Выразим «зет»: , после чего уравнение распадается на две функции:
– задаёт верхнюю полусферу;
– задаёт нижнюю полусферу.
Область определения функции – это её ортогональная проекция на плоскость . Очевидно, что областью определения наших функций является круг с центром в начале координат радиуса 2.
Неравенство определяет шар с центром в начале координат радиуса 2. Подставим координаты точек в данное неравенство:
1) |
2) |
Следующее задание для самостоятельного решения:
Задача 175
Найти область определения функции двух переменных и построить соответствующую поверхность.
Решение и ответ в конце книги.
Кстати, наша планета, кто не знает, имеет форму эллипсоида. Чуть-чуть-чуть, но Земля – таки не шар.
6.4. Коническая поверхность
6.2. Цилиндрические поверхности
| Оглавление |
Автор: Aлeксaндр Eмeлин
Эллипсоид. Построение по точкам
|
|
|
|||||||||||||||||||||||||||||||||||||
Через край с вертикальными эллипсоидами
Think Round К Дэйв Саут
Набросок концепции калькулятора вертикального эллипсоидного купола. Мы можем описать короткие, сплюснутые над центром эллипсоиды до высоких, почти полных вытянутых эллипсоидов.
Дэйв Саут
Надувные формы являются основными компонентами конструкции монолитного купола. Если он раздувается, его можно построить… наверное. В конструкции купола преобладают две основные формы — сфера и полуэллипсоид. Однако это далеко не вся палитра дизайна. Иногда нам нужно выйти за рамки основ. или в этом случае за пределами половины эллипсоида.
Вертикальный эллипсоид имеет круглое основание и эллиптическое поперечное сечение. Другими словами, он выглядит как круг, если смотреть сверху, и как эллипс, если смотреть с любой стороны. В отличие от калькулятора полуэллипсоида, мы можем указать любую часть эллипсоида. Может быть, нам просто нужна вершина, чуть больше половины, или почти целый эллипсоид — короткий или высокий, узкий или широкий.
Для этого предназначен Калькулятор вертикального эллипсоидного купола. Это дает полный контроль над общей формой эллипсоида и тем, где эта форма пересекает землю. Базовый код для этого калькулятора используется совместно с калькулятором полуэллипсоида. Они оба повторяют более 36 000 срезов формы, чтобы найти площадь поверхности, и результат оказывается более точным, чем наш старый калькулятор — от восьми до девяти значащих цифр вместо трех-четырех.
Это дает полный контроль над общей формой эллипсоида и тем, где эта форма пересекает землю. Базовый код для этого калькулятора используется совместно с калькулятором полуэллипсоида. Они оба повторяют более 36 000 срезов формы, чтобы найти площадь поверхности, и результат оказывается более точным, чем наш старый калькулятор — от восьми до девяти значащих цифр вместо трех-четырех.
The Palapa Pineapple в Белизе представляет собой четырехэтажный вытянутый эллипсоидный купольный дом с открытым первым этажом, жилой площадью на следующих трех уровнях, а затем крытой террасой на крыше. Форма лучше всего подходила для земли и нужд домовладельцев.
Дэйв и Мэри Спеллингс
Так когда же его использовать?
Для работы с базовыми конструкциями куполов проще и доступнее использовать сферический или эллипсоидный калькулятор. Начните с этого. Нужна крупная коммерческая структура, воспользуйтесь сферическим калькулятором. Хотите построить дом в одном куполе, попробуйте калькулятор эллипсоида.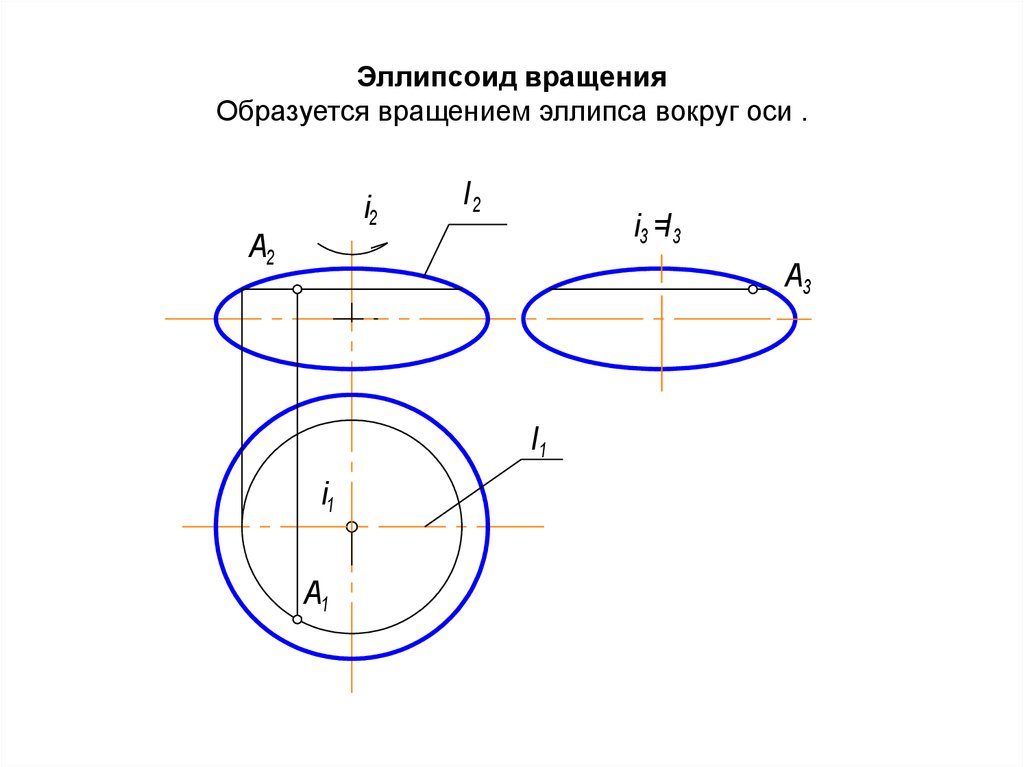 Но пока вы работаете над зданием своей мечты, вы можете столкнуться с идеями, которые выходят за рамки простого купола.
Но пока вы работаете над зданием своей мечты, вы можете столкнуться с идеями, которые выходят за рамки простого купола.
Например, Дейв и Мэри Спеллингс хотели купить купольный дом в Белизе. Они хотели 360-градусный вид на океан и выделяющийся дом. Базовые конструкции не помешали бы этому. В конце концов, они остановились на форме ананаса. Теперь мы находимся на территории вертикального эллипсоида. Основная форма представляет собой вытянутый эллипсоид высотой в четыре этажа, увенчанный открытой смотровой площадкой и прекрасным видом на океан.
Как насчет дизайна в стиле НЛО или дома, который «врезается» в склон холма? Может быть, специальный купол в составе многокупольного комплекса? Как насчет дизайна дома хоббита, который похоронен и выглядит как что-то прямо из графства? А еще есть нестандартные соединенные между собой купола. Нам нужны оценки нескольких куполов, прежде чем мы начнем проектировать соединения.
Все эти конструкции требуют более сложных расчетов.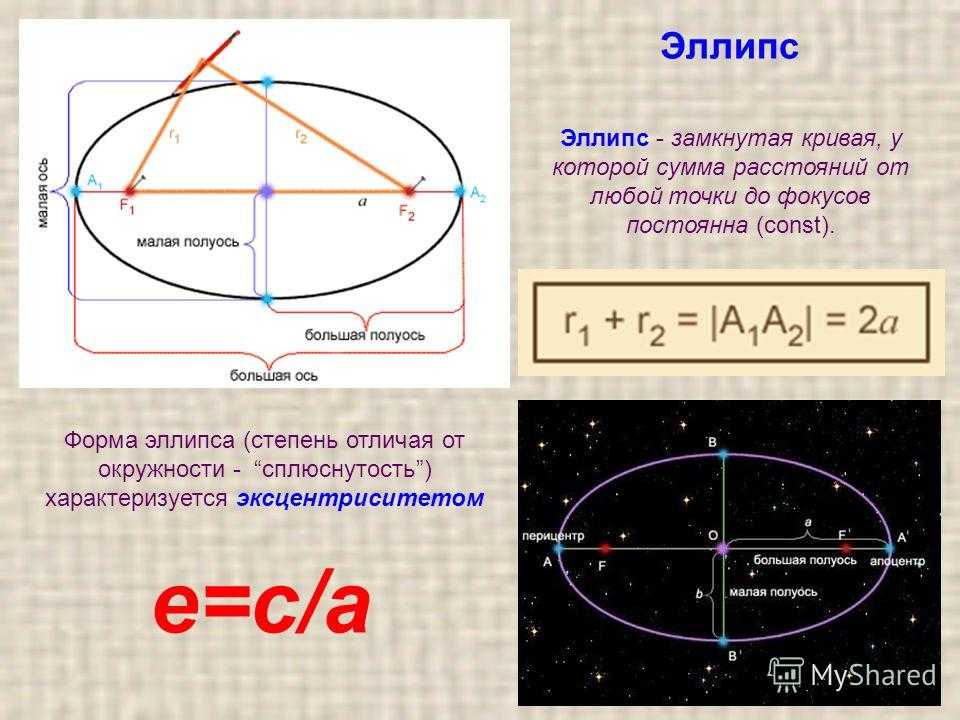 Таким образом, хотя мы не можем использовать калькулятор вертикального эллипсоида для каждого купола, когда он необходим, он бесценен. Попробуйте.
Таким образом, хотя мы не можем использовать калькулятор вертикального эллипсоида для каждого купола, когда он необходим, он бесценен. Попробуйте.
Готовый калькулятор вертикального эллипсоидного купола
Дэйв Саут
Три способа выложить эллиптическую кривую
Крыша из кривых доказывает правильность техники: в составе бригады, работающей над восстановлением Консерватории цветов в Сан-Франциско, автор смог усовершенствовать свои навыки создания эллиптических стропил.
Как определено в словаре Merriam-Webster Collegiate Dictionary, эллипс — это «замкнутая плоская кривая, образованная точкой, движущейся таким образом, что сумма расстояний от нее до двух фиксированных точек [фокусов] является постоянной; плоское сечение прямого кругового конуса, представляющего собой замкнутую кривую». Понятно? К счастью, гораздо проще увидеть эллипс, чем понять его определение. Просто обрежьте дюбель под углом 90° с одного конца и до 45° с другого. Квадратный разрез создает круг с одинаковым радиусом, равным ширине и высоте. Конец, срезанный под углом 45°, представляет собой эллипс, ширина которого превышает высоту.
Конец, срезанный под углом 45°, представляет собой эллипс, ширина которого превышает высоту.
Этот эллипс является примером геометрии некоторых более крупных компонентов здания. Поскольку эти кривые поддаются количественной оценке, их подъем и уклон можно определить, используя правила каркаса крыши. Например, сводчатый потолок с общей секцией размером 12 дюймов. радиус четверти будет иметь угловую стойку или ребро, представляющее собой четверть эллипса с подъемом 12 дюймов и длиной 17 дюймов.
Существует несколько способов выложить эллипс. Здесь я опишу три, используя соотношение подъема к пробежке 12:17. Первый — это строковый метод, наиболее знакомый. Используйте веревку, которая не будет растягиваться, хотя более длинные нити имеют тенденцию растягиваться, несмотря ни на что. Длину нити можно найти по формуле, но иногда проще просто натянуть нить вокруг двух фокусов и до известной точки на кривой, например, в этом примере, на 12 дюймов вверх по малой оси.
Второй метод, основанный на решительных подъемах и бегах, заключается в использовании трамвая. Трамвай движется вокруг квадратного угла куска фанеры или другого подходящего материала. Нарисованная траммелем кривая дает правильный эллипс для обычного бедра на 12-дюймовом. перекрытие с радиальным сводом или крыша с криволинейными стропилами. Чтобы нарисовать вальму на восьмиугольной крыше, траммель устанавливается с 12-дюймовым. рост и 13-в. бегать.
Трамвай движется вокруг квадратного угла куска фанеры или другого подходящего материала. Нарисованная траммелем кривая дает правильный эллипс для обычного бедра на 12-дюймовом. перекрытие с радиальным сводом или крыша с криволинейными стропилами. Чтобы нарисовать вальму на восьмиугольной крыше, траммель устанавливается с 12-дюймовым. рост и 13-в. бегать.
Третий — арифметическое построение, также известное как лофтинг, которое можно применить к любой кривой. Этот метод удобен, когда вам нужно получить ребро или впадину из существующей кривой, не имеющей количественного определения, или если эллипс слишком велик, чтобы его можно было нарисовать с помощью трамвая. Во время реставрации Консерватории цветов в Сан-Франциско оба сценария были правдой. Мы нарисовали сетку из 12 дюймов. квадраты на полу, а затем рассчитали форму изогнутых общих стропил, вальм и ендов. После того, как бедра и долины были обрезаны по форме, мы обрезали подложку с изменяющимся двойным скосом, который начинался с двух надрезов под 45° на нижнем отвесном конце кривой и уменьшался до одного плоского края на верхнем, ровном конце.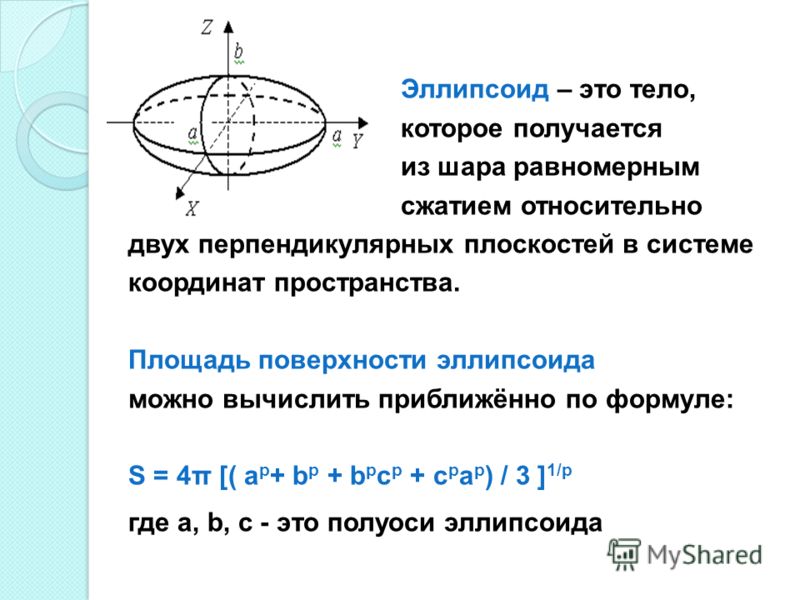
Что такое эллипс?
Конец прямоугольного дюбеля представляет собой окружность, в которой подъем (высота) и ход (ширина) одинаковы, что дает одинаковый радиус. Но обрежьте дюбель под углом 45°, и конец будет эллипсом, ширина которого больше высоты. Его радиус переменный.
Используйте веревку
Нарисуйте эллипс с помощью веревки, двух булавок и карандаша. Сначала нарисуйте горизонтальную линию и отметьте центральную точку. Затем определите подъем и пробег эллипса. Точки привязки струны, называемые фокусами, расположены по следующему уравнению: фокусы = √(run² – подъем²). Длину строки можно рассчитать следующим образом: длина строки = 2(фокусы + пробег). Найдя центральную точку и фокусы, прикрепите ненатягивающуюся нить нужной длины к гвоздям или шурупам, вбитым в фокусы. Используя веревку, удерживающую карандаш, нарисуйте эллипс.
Используйте палочку
Просверлите отверстие для карандаша в середине 1×2. От центральной линии карандаша измерьте расстояние желаемого подъема (координата y) эллипса (например, 12 дюймов) и вбейте шуруп или гвоздь в траверсу. В противоположном направлении измерьте расстояние прогона (координата x; например, 17 дюймов) и установите еще один шуруп или гвоздь. (Для точности штифты должны находиться сразу за пределами измеренной точки.)
В противоположном направлении измерьте расстояние прогона (координата x; например, 17 дюймов) и установите еще один шуруп или гвоздь. (Для точности штифты должны находиться сразу за пределами измеренной точки.)
Чтобы нарисовать эллипс, совместите штифты и карандаш вдоль вертикального края заготовки. Удерживая штифты плотно прижатыми к краям фанеры, переместите нижний штифт (подъем) вправо, когда верхний штифт (выступ) опустится по вертикали.
Используйте сетку
Если эллипс слишком велик, чтобы его можно было нарисовать с помощью трамплина, его можно нарисовать с помощью алгебраической формулы. Начните с рисования сетки на листе бумаги подходящего размера, листе фанеры или черновом полу. Если вы разделите горизонтальную ось на 20 частей, вы будете достаточно точны. Чтобы нарисовать сопутствующий вальм или ендову к изогнутому обычному стропилу, вам нужно сначала нарисовать общее. Для иллюстрации мы будем использовать четверть радиуса для описания общего, которое можно нарисовать, повернув дугу от пересечения осей x и осей y.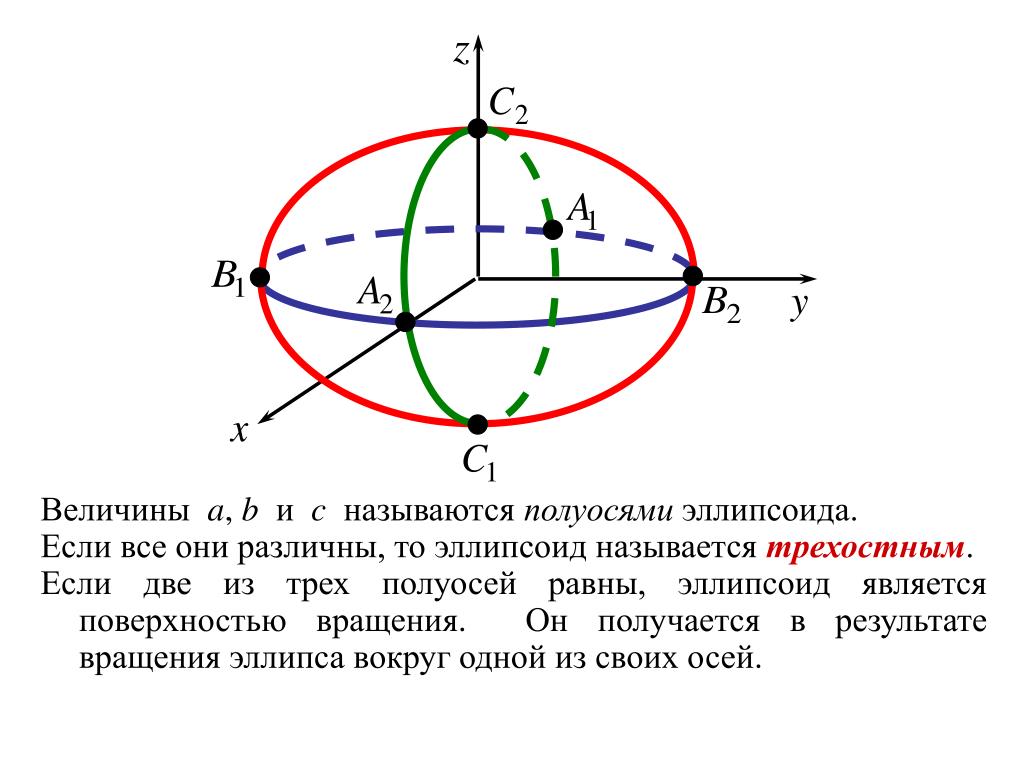

 Первые полторы тысяч разложений.
Первые полторы тысяч разложений.

 Угол между ними.
Угол между ними.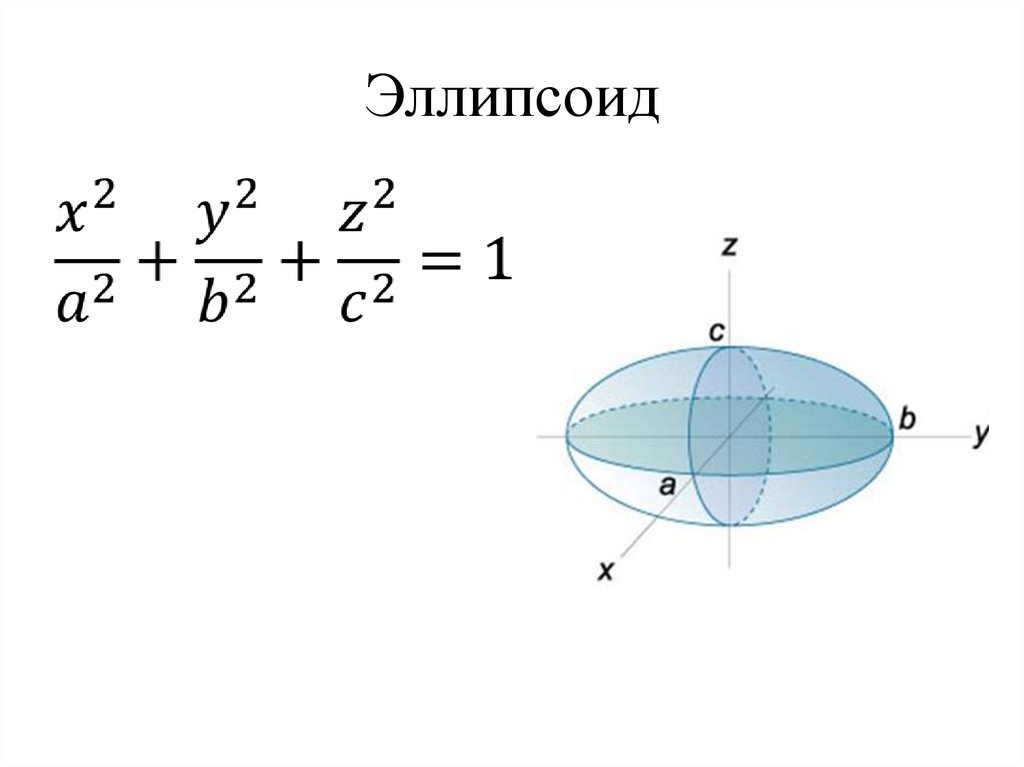 Матрица смежности онлайн
Матрица смежности онлайн