Лекция 15. Эллипс
Лекции по алгебре и геометрии. Семестр 1.
Лекция 15. Эллипс.
Краткое содержание: определение эллипса, основная терминология, каноническая для эллипса система координат и каноническое уравнение эллипса, параметрические уравнения эллипса, эллипс как результат сжатия окружности, касательная к эллипсу, зеркальное свойство эллипса, директрисы и фокальный параметр эллипса, второе определение эллипса.
Глава 15. Эллипс.
п.1. Основные определения.
Определение. Эллипсом называется ГМТ плоскости сумма расстояний которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная.
рис.1.
Определение. Расстояние от произвольной точки М плоскости до фокуса эллипса называется фокальным радиусом точки М.
Обозначения: – фокусы эллипса, – фокальные радиусы точки М.
По
определению эллипса, точка М является
точкой эллипса тогда и только тогда,
когда – постоянная величина.
. (1)
Заметим, что .
По определению эллипса, его фокусы есть фиксированные точки, поэтому расстояние между ними есть также величина постоянная для данного эллипса.
Определение. Расстояние между фокусами эллипса называется фокусным расстоянием.
Обозначение: .
Из треугольника следует, что , т.е.
.
Обозначим через b число равное , т.е.
. (2)
Определение. Отношение
(3)
называется эксцентриситетом эллипса.
Введем на данной плоскости систему координат, которую мы будем называть канонической для эллипса.
Определение. Ось, на которой лежат фокусы эллипса, называется фокальной осью.
Построим
каноническую для эллипса ПДСК, см. рис.2.
рис.2.
В качестве оси абсцисс выбираем фокальную ось, а ось ординат проводим через середину отрезка перпендикулярно фокальной оси.
рис.2.
Тогда фокусы имеют координаты , .
п.2. Каноническое уравнение эллипса.
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
. (4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любое решение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и из определения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.
1)
Пусть точка М(х, у) является точкой
эллипса, т. е. сумма ее фокальных радиусов
равна 2а:
е. сумма ее фокальных радиусов
равна 2а:
.
Воспользуемся формулой расстояния между двумя точками на координатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
, , откуда получаем:
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
.
Сокращая, получаем:
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
.
Возводим в квадрат
.
Раскрываем скобки и сокращаем на :
,
откуда получаем:
.Используя равенство (2), получаем:
.
Разделив последнее равенство на , получаем равенство (4), ч.т.д.
2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.
Тогда из (4) следует:
.
Подставляем это равенство в выражение для фокальных радиусов точки М:
.
Здесь мы воспользовались равенством (2) и (3).
Таким образом, . Аналогично, .
Теперь заметим, что из равенства (4) следует, что
или и т.к. , то отсюда следует неравенство:
.
Отсюда, в свою очередь, следует, что
или и
, . (5)
Из равенств (5) следует, что , т.е. точка М(х, у) является точкой эллипса, ч.т.д.
Теорема доказана.
Определение. Уравнение (4) называется каноническим уравнением эллипса.
Определение. Канонические для эллипса оси координат называются главными осями эллипса.
Определение. Начало канонической для эллипса системы координат называется центром эллипса.
п.3. Свойства эллипса.
Теорема. (Свойства эллипса.)
1. В канонической для эллипса системе координат, все
точки эллипса находятся в прямоугольнике
,
.
2. Точки лежат на
эллипсе.
3. Эллипс является кривой, симметричной относительно
своих главных осей.
4. Центр эллипса является его центром симметрии.
Доказательство. 1, 2) Сразу же следует из канонического уравнения эллипса.
3, 4) Пусть М(х, у) – произвольная точка эллипса. Тогда ее координаты удовлетворяют уравнению (4). Но тогда координаты точек также удовлетворяют уравнению (4), и, следовательно, являются точками эллипса, откуда и следуют утверждения теоремы.
Теорема доказана.
рис.3.
Определение. Величина 2а называется большой осью эллипса, величина а называется большой полуосью эллипса.
Определение. Величина 2b называется малой осью эллипса, величина b называется малой полуосью эллипса.
Определение. Точки пересечения эллипса с его главными осями называются вершинами эллипса.
Замечание.
Эллипс можно построить следующим
образом. На плоскости в фокусы «забиваем
по гвоздю» и закрепляем на них нить
длиной
. Затем берем карандаш и с его помощью
натягиваем нить. Затем передвигаем
карандашный грифель по плоскости, следя
за тем, чтобы нить была в натянутом
состоянии.
Затем берем карандаш и с его помощью
натягиваем нить. Затем передвигаем
карандашный грифель по плоскости, следя
за тем, чтобы нить была в натянутом
состоянии.
Из определения эксцентриситета следует, что
Зафиксируем число а и устремим число с к нулю. Тогда при , и . В пределе мы получаем
или – уравнение окружности.
Таким образом, мы можем считать, что окружность есть эллипс с нулевым эксцентриситетом.
Устремим теперь . Тогда , и мы видим, что в пределе эллипс вырождается в отрезок прямой в обозначениях рисунка 3.
п.4. Параметрические уравнения эллипса.
Теорема. Пусть – произвольные действительные числа. Тогда система уравнения
, (6)
является параметрическими уравнениями эллипса в канонических для эллипса системе координат.
Доказательство.
Достаточно доказать, что система
уравнений (6) равносильна уравнению (4),
т. е. они имеют одно и то же множество
решений.
е. они имеют одно и то же множество
решений.
1) Пусть (х, у) – произвольное решение системы (6). Разделим первое уравнение на а, второе – на b, возводим оба уравнения в квадрат и складываем:
.
Т.е. любое решение (х, у) системы (6) удовлетворяет уравнению (4).
2) Обратно, пусть пара (х, у) является решением уравнения (4), т.е.
.
Из этого равенства следует, что точка с координатами лежит на окружности единичного радиуса с центром в начале координат, т.е. является точкой тригонометрической окружности, которой соответствует некоторый угол :
рис.4.
Из определения синуса и косинуса сразу же следует, что
, , где , откуда и следует, что пара (х, у) является решением системы (6), ч.т.д.
Теорема доказана.
Замечание.
Эллипс можно получить в результате
равномерного «сжатия» окружности
радиуса а к оси абсцисс.
Пусть – уравнение окружности с центром в начале координат. «Сжатие» окружности к оси абсцисс есть ни что иное, как преобразование координатной плоскости, осуществляемое по следующему правилу. Каждой точке М(х, у) поставим в соответствие точку этой же плоскости , где , – коэффициент «сжатия».
рис.5.
При этом преобразовании каждая точка окружности «переходит» в другую точку плоскости, имеющую ту же самую абсциссу, но меньшую ординату. Выразим старую ординату точки через новую:
и подставим в уравнение окружности:
.
Отсюда получаем:
. (7)
Отсюда
следует, что если до преобразования
«сжатия» точка М(х, у) лежала на
окружности, т.е. ее координаты удовлетворяли
уравнению окружности, то после
преображования «сжатия» эта точка
«перешла» в точку
,
координаты которой удовлетворяют
уравнению эллипса (7).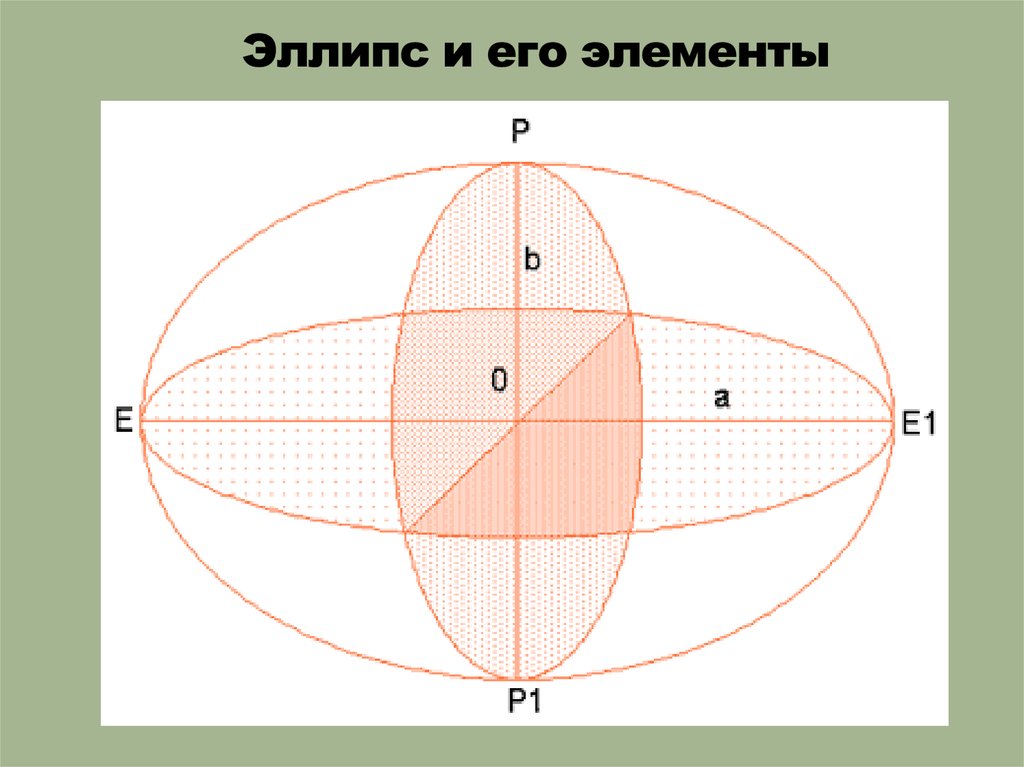
.
рис.6.
п.5. Касательная к эллипсу.
Теорема. Пусть – произвольная точка эллипса
.
Тогда уравнение касательной к этому эллипсу в точке имеет вид:
. (8)
Доказательство. Достаточно рассмотреть случай, когда точка касания лежит в первой или второй четверти координатной плоскости: . Уравнение эллипса в верхней полуплоскости имеет вид:
. (9)
Воспользуемся уравнением касательной к графику функции в точке :
, (10)
где – значение производной данной функции
в точке
.
Эллипс в первой четверти можно
рассматривать как график функции (8). Найдем ее производную и ее значение в
точке касания:
Найдем ее производную и ее значение в
точке касания:
,
. Здесь мы воспользовались тем, что точка касания является точкой эллипса и поэтому ее координаты удовлетворяют уравнению эллипса (9), т.е.
.
Подставляем найденное значение производной в уравнение касательной (10):
,
откуда получаем:
или
.
Отсюда следует:
.
Разделим это равенство на :
.
Осталось заметить, что , т.к. точка принадлежит эллипсу и ее координаты удовлетворяют его уравнению.
Аналогично доказывается уравнение касательной (8) в точке касания, лежащей в третьей или четвертой четверти координатной плоскости.
И, наконец, легко убеждаемся, что уравнение (8) дает уравнение касательной в точках , :
или , и или .
Теорема доказана.
п.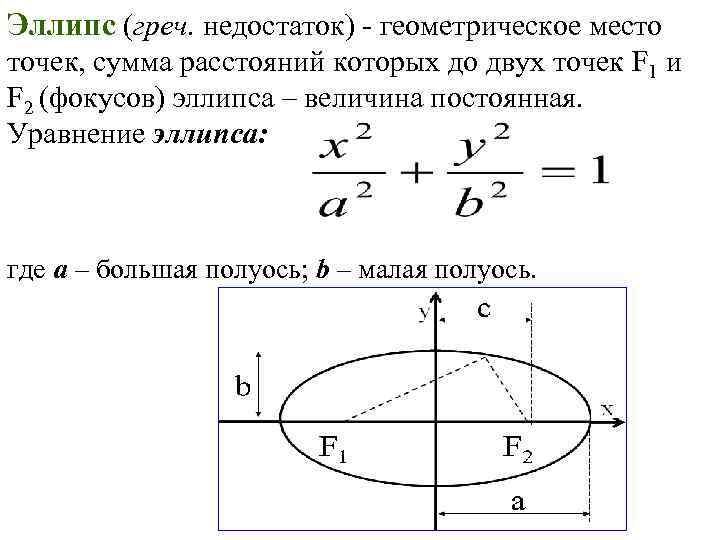 6.
Зеркальное свойство эллипса.
6.
Зеркальное свойство эллипса.
Теорема. Касательная к эллипсу имеет равные углы с фокальными радиусами точки касания.
рис.7.
Пусть – точка касания, , – фокальные радиусы точки касания, Р и Q – проекции фокусов на касательную, проведенную к эллипсу в точке .
Теорема утверждает, что
. (11)
Это равенство можно интерпретировать как равенство углов падения и отражения луча света от эллипса, выпущенного из его фокуса. Это свойство получило название зеркального свойства эллипса:
Луч света, выпущенный из фокуса эллипса, после отражения от зеркала эллипса проходит через другой фокус эллипса.
Доказательство теоремы. Для доказательства равенства углов (11) мы докажем подобие треугольников и , в которых стороны и будут сходственными. Так как треугольники прямоугольные, то достаточно доказать равенство
. (12)
(12)
Так как по построению – расстояние от фокуса до касательной L (см. рис.7), . Воспользуемся формулой расстояния от точки до прямой на плоскости:
.
Так как уравнение касательной к эллипсу в точке имеет вид
,
то
,
и
.
Здесь мы воспользовались формулами (5) для фокальных радиусов точки эллипса.
Теорема доказана.
Второе доказательство теоремы:
, , – нормальный вектор касательной L.
. Отсюда, .
Аналогично находим, и , ч.т.д.
п.7. Директрисы эллипса.
Определение. Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения
или . (13)
рис.8.
Теорема.
Пусть М – произвольная точка эллипса,
, – ее фокальные радиусы, – расстояние от точки М до левой
директрисы, – до правой.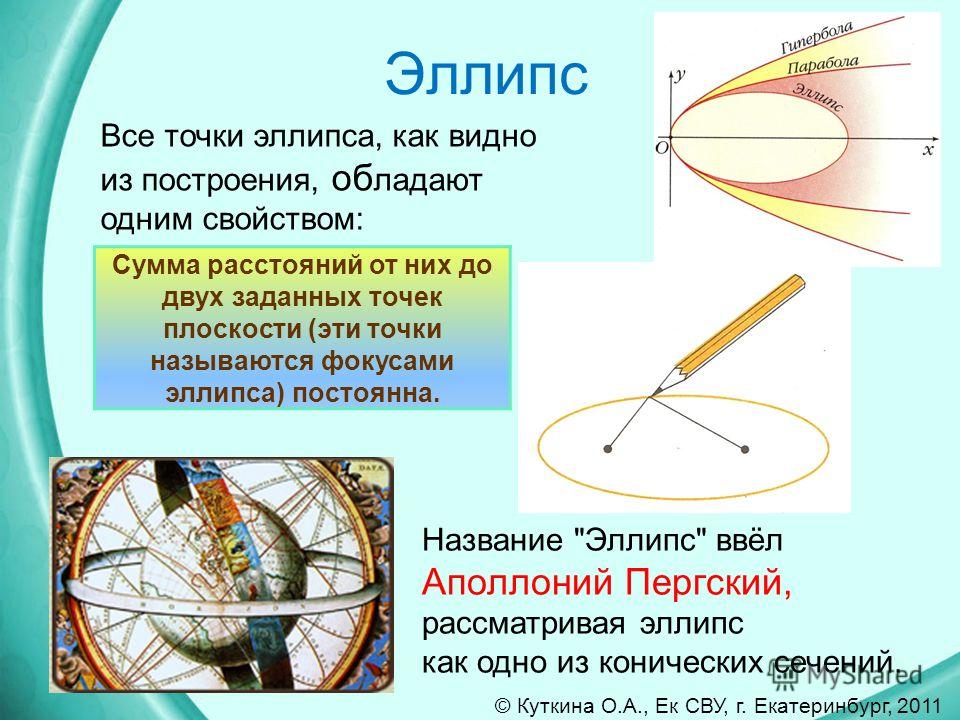 Тогда
Тогда
, (14)
где – эксцентриситет эллипса.
Доказательство.
рис.9.
Пусть М(х, у) – координаты произвольной точки эллипса. Тогда
, ,
откуда и следуют равенства (14).
Теорема доказана.
п.8. Фокальный параметр эллипса.
Определение. Фокальным параметром эллипса называется длина перпендикуляра, восстановленного в его фокусе до пересечения с эллипсом.
Фокальный параметр принято обозначать буквой р.
рис.9.
Из определения следует, что фокальный параметр
.
Теорема. Фокальный параметр эллипса равен
. (15)
Доказательство. Так как точка N(–с; р) явяляется точкой эллипса , то ее координаты удовлетворяют его уравнению:
.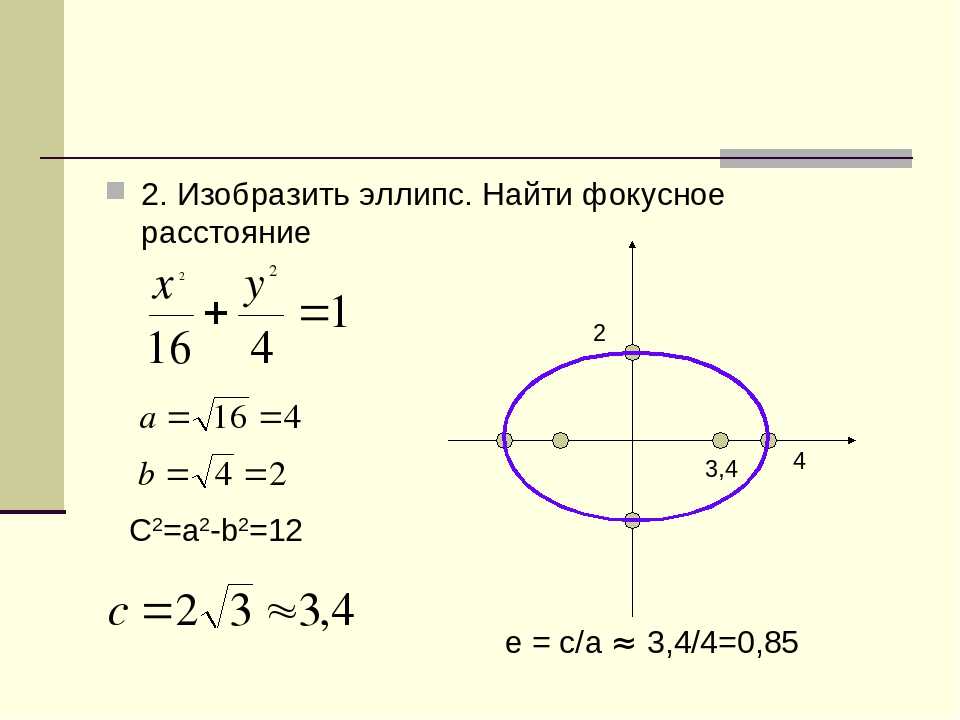
Отсюда находим
,
откуда и следует (15).
Теорема доказана.
п.9. Второе определение эллипса.
Теорема из п.7. может служить определением эллипса.
Определение. Эллипсом называется ГМТ для которых отношение расстояния до фиксированной точки плоскости, называемой фокусом, к расстоянию до фиксированной прямой, называемой директрисой, есть величина постоянная меньше единицы и называемая его эксцентриситетом:
.
рис.10.
Разумеется, в этом случае, первое определение эооипса является теоремой, которую необходимо доказывать.
4.5. Эллипс Канонические уравнения эллипса кратко Линейная…
Привет, мой друг, тебе интересно узнать все про эллипс, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
эллипс, канонические уравнения эллипса , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.
эллипс (др.-греч. ἔλλειψις «опущение; нехватка, недостаток (эксцентриситета до 1)») — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость.
Одной из трех составляющих «Триады Менехма» является Эллипс.
Ее открыл в IV веке до н. э. древнегреческий математик Менехм, пересекая разного вида конусы (остроугольный, прямоугольный и тупоугольный)
плоскостью, перпендикулярной образующей. В итоге ему удалось свести решение задачи об удвоении куба к нахождению точек пересечения двух
парабол. Более столетия конические сечения не имели собственных названий (указывали лишь способ получения кривых, например, эллипс —
«сечение остроугольного конуса»).
Эллипс как коническое сечение, его фокусы и директрисы, получаемые геометрически с помощью шаров Данделена.
Шары Данделена — сферы, участвующие в геометрическом построении, которое связывает планиметрическое определение эллипса, гиперболы и параболы через фокусы с их стереометрическим определением как сечения конуса. Предложены Данделеном в 1822 году.
Сферы Данделина можно использовать для элегантных современных доказательств двух классических теорем, известных Аполлонию Пергскому . Первая теорема состоит в том, что замкнутое коническое сечение (т.е. эллипс ) — это геометрическое место точек, такое что сумма расстояний до двух фиксированных точек (фокусов) постоянна. Вторая теорема заключается в том, что для любого конического сечения расстояние от фиксированной точки (фокуса) пропорционально расстоянию от фиксированной линии ( директрисы ), а коэффициент пропорциональности называется эксцентриситетом .
Коническое сечение имеет по одной сфере Данделина для каждого фокуса. Эллипс состоит из двух сфер Данделина, соприкасающихся с одной и той же вершиной конуса, в то время как у гиперболы две сферы Данделина касаются противоположных вершин.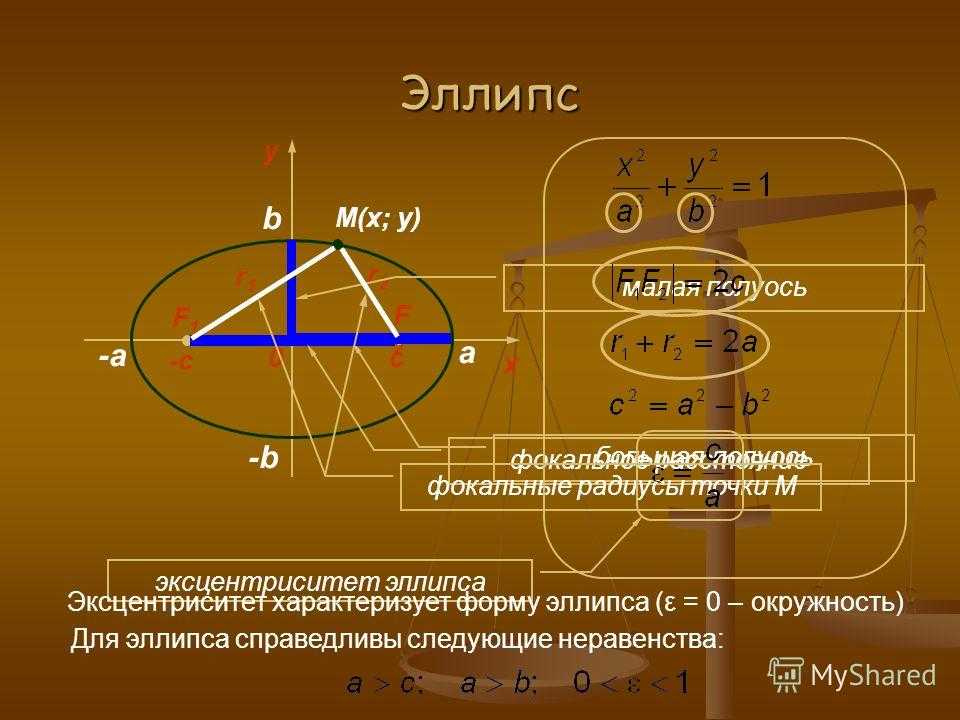 Парабола имеет только один шары данделена.
Парабола имеет только один шары данделена.
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.
Эллипс — геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек и (называемых фокусами) постоянна и больше расстояния между фокусами, то есть
, причем .
Другие определения
Эллипс также можно определить как:
- фигуру, которую можно получить из окружности, применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость
- пересечение плоскости и кругового цилиндра.
Рис. 5
— каноническое уравнение эллипса (рис. 5),— большая полуось,
— малая полуось,
— левый и правый фокусы,
— эксцентриситет,— левая и правая директрисы,
— левый и правый фокальные радиусы точки ,
— расстояния от точки P до левой и правой директрисы.
Приближенные формулы для периметра
Максимальная погрешность этой формулы при эксцентриситете эллипса (соотношение осей ) . Об этом говорит сайт https://intellect.icu . Погрешность всегда положительна.
Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула: , где Максимальная погрешность этой формулы при эксцентриситете эллипса (соотношение осей {\displaystyle \approx 1/5}) Погрешность также всегда положительна.
Существенно лучшую точность при обеспечивает формула Рамануджана:
При эксцентриситете эллипса (соотношение осей ) погрешность составляет . Погрешность всегда отрицательна.
Еще точней оказалась вторая формула Рамануджана:
Точные формулы для периметра
Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:
Альтернативная формула
где — Арифметико-геометрическое среднее 1 и , а — модифицированное арифметико-геометрическое среднее 1 и , которое было введено С.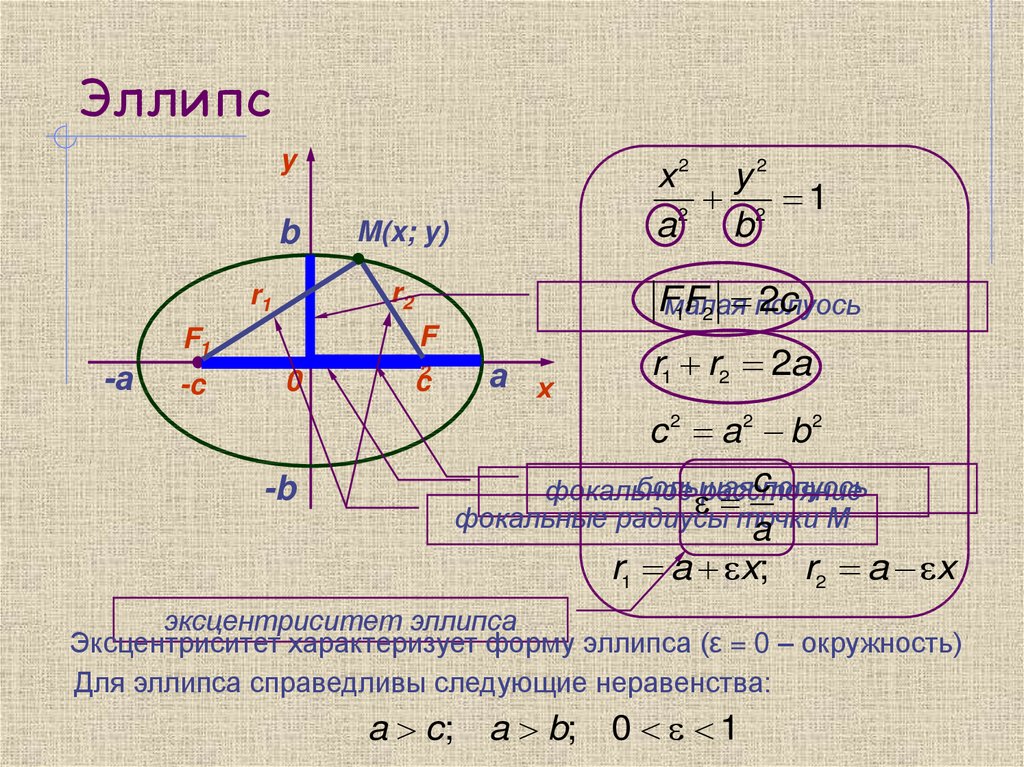 Ф. Адлаем в статье 2012 года.
Ф. Адлаем в статье 2012 года.
Площадь эллипса и его сегмента
Площадь эллипса вычисляется по формуле
Площадь сегмента между дугой[en], выпуклой влево, и вертикальной хордой, проходящей через точки и , можно определить по формуле :
Если эллипс задан уравнением , то площадь можно определить по формуле
Другие свойства
- Оптические
- Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
- Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
- Если и — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой равен углу между этой касательной и прямой .
- Прямая, проведенная через середины отрезков, отсеченных двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса.
 Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эквивалентная формулировка: через середины двух любых параллельных хорд эллипса проходит какой-либо диаметр эллипса. В свою очередь, любой диаметр эллипса всегда проходит через центр эллипса.
- Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
- Точки пересечения эллипса с осями являются его вершинами.
- Эксцентриситет эллипса, то есть отношение характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю: {\displaystyle F_{1}F_{2}=0}), то эллипс вырождается в окружность.
- Экстремальные свойства
- Если — выпуклая фигура и — вписанный в -угольник максимальной площади, то
где обозначает площадь фигуры .
- Более того: равенство достигается в том и только в том случае, если {\displaystyle F} ограничено эллипсом.
- Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину.
- Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение
- Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (все время касаясь ее) а второй конец лестницы будет скользить по полу (все время касаясь его), тогда любая фиксированная точка лестницы (не на ее концах), будет двигаться по дуге некоторого эллипса. Это свойство остается верным, если мы возьмем точку не внутри лестницы-отрезка, а на ее мыслимом продолжении. Последнее свойство используется в описанном выше[⇦] эллипсографе.
- Касательная, проходящая через точку , принадлежащую эллипсу, имеет следующее уравнение:
Применение эллипса
с помощью Эллипса сделали революционное открытие в астрономии
В XVI веке математик и астроном древности Кеплер доказал, что каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце
вычисление хода отражения
движенее материальной точки по эллиптической кривой
канонические уравнения эллипса и гиперболы
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про эллипс Надеюсь, что теперь ты понял что такое эллипс, канонические уравнения эллипса
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Линейная алгебра и аналитическая геометрия
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Линейная алгебра и аналитическая геометрия
Кривые второго порядка. Эллипс: формулы и задачи
- Понятие о кривых второго порядка
- Эллипс, заданный каноническим уравнением
- Решить задачи на эллипс самостоятельно, а затем посмотреть решение
- Продолжаем решать задачи на эллипс самостоятельно
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются
канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений,
этому будет посвящён пример 1 задач с эллипсами.
К ним легко перейти от общих уравнений,
этому будет посвящён пример 1 задач с эллипсами.
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и
(- a, О), а ось ординат — в точках (b, О) и
(- b, О). Эти четыре точки называются вершинами эллипса. Отрезок
между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат —
малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Эти четыре точки называются вершинами эллипса. Отрезок
между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат —
малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b, то уравнение эллипса принимает вид . Это уравнение окружности радиуса a, а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a, если сжать её в a/b раз вдоль оси Oy.
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является
каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5, меньшая полуось — это b = 4. Получаем каноническое уравнение эллипса:
.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кривые второго порядка
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
Число
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса.
Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень
вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена
выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда
меньше единицы.
Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда
меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13. Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
посмотреть правильное решение и ответ,
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
посмотреть правильное решение и ответ,
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
посмотреть правильное решение и ответ.
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и — расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется
найти эксцентриситет эллипса, т. е. .
Все данные для этого есть.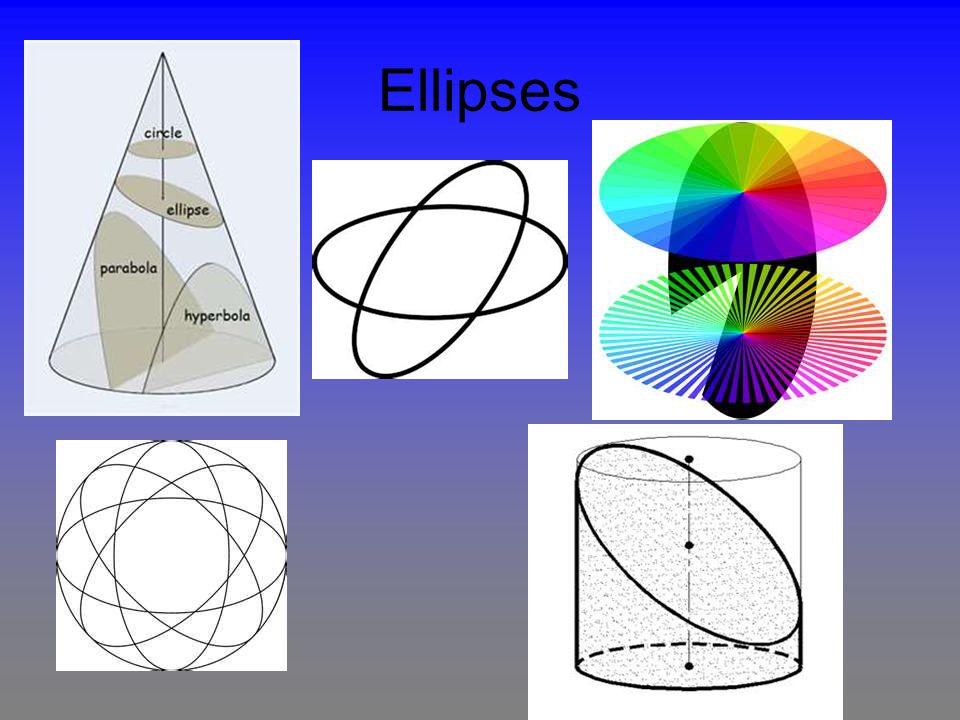 Вычисляем:
Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице
(точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое
свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают
касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса,
после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта,
наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют
эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в
другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле
расстояние велико.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кривые второго порядка
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
Гипербола
Парабола
эллипсов: Введение | Purplemath
Найти информацию из eqnНайти eqn из infoWord Проблемы
Purplemath
Что такое эллипс?
Эллипс, неофициально, представляет собой овал или «сплющенный» круг. С физической точки зрения эллипс — это фигура, которую вы можете нарисовать на песке, выполнив следующий процесс: воткните в песок две палочки. Возьмите кусок веревки и сформируйте петлю, которая будет достаточно большой, чтобы охватить две палочки и при этом иметь небольшой провис. Возьмите третью палку, зацепите ее за петлю веревки, туго натяните петлю, оттянув палку от первых двух палочек, и протащите эту третью палку по песку на самое дальнее расстояние, которое позволяет петля. Получившаяся фигура, нарисованная на песке, представляет собой эллипс.
Получившаяся фигура, нарисованная на песке, представляет собой эллипс.
Содержание продолжается ниже
MathHelp.com
(С технической точки зрения эллипс отличается от овала тем, что овал больше похож на яйцо. имеет форму яйцевидной или овальной формы.] Яйцо на одном конце заостреннее, чем на другом, эллипс одинаково круглый на каждом конце.)
Какие важные термины используются для обозначения эллипсов?
Каждая из двух палочек, которую вы сначала воткнули в песок, является «фокусом» эллипса; вместе они называются «очагами» (FOH-siy). Если вы проведете линию на песке «сквозь» эти две палочки от одного конца эллипса к другому, это обозначит «большую» ось эллипса. Точки, где большая ось касается эллипса, являются «вершинами» эллипса. Точка посередине между двумя палочками является «центром» эллипса.
Если вы проведете линию через этот центр, перпендикулярно большой оси и от одной стороны эллипса к другой, это отметит «малую» ось. Точки, где малая ось касается эллипса, являются «ко-вершинами». Полуось, идущая от центра к эллипсу, называется «большой полуосью» или «малой полуосью», в зависимости от того, половину какой оси вы берете.
Полуось, идущая от центра к эллипсу, называется «большой полуосью» или «малой полуосью», в зависимости от того, половину какой оси вы берете.
Расстояние от центра до любого фокуса является фиксированным значением c . Расстояние от центра до вершины является фиксированным значением и . Значения a и c будут варьироваться от одного эллипса к другому, но они фиксированы для любого данного эллипса. Я сохраняю значение этих двух букв, неправильно произнося фразу «фокусы для c » как «FOH-ciy foh SEE», чтобы напомнить мне, что c относится к фокусу. Затем другая буква ( a ) предназначена для другого типа точки (вершины).
Длина большой полуоси составляет a , а длина всей большой оси составляет 2 a , а расстояние между фокусами 2 c . Итак, теперь у нас есть отношения для a и c , что заставляет задаться вопросом: «Что случилось с b »? Три буквы связаны уравнением b 2 = a 2 − c 2 или, альтернативно (в зависимости от вашей книги или преподавателя), уравнением b 4 в 2 = а 2 . (Для доказательства соотношения требуются страницы и страницы алгебраических вычислений, так что просто поверьте мне, что уравнение верно. Можно также показать — мучительно — что b также является длиной малой полуоси, поэтому расстояние через эллипс в «более коротком» направлении 2 b . Да, теорема Пифагора участвует в доказательстве этого материала. Да, это те же самые буквы, которые используются в теореме Пифагора. Нет, это , а не то же самое, что и Теорема Пифагора. Да, это очень запутанно. Примите это, убедитесь, что вы запомнили правильное соотношение перед следующим тестом, а затем двигайтесь дальше.) Для эллипса шире, чем высота, с центром в точке ( h , k ), с вершинами a единиц по обе стороны от центра и фокусами c единиц по обе стороны от центра, эллипс уравнение: Для эллипса, длина которого больше ширины, с центром в точке ( h , k ), с вершинами a единиц выше и ниже центра и фокусами c единиц выше и ниже центра , уравнение эллипса: Уравнение эллипса в конической форме всегда равно «=1». Обратите внимание, что в обоих приведенных выше уравнениях h всегда оставалось с x , а k всегда оставалось с y . Единственное, что изменилось между двумя уравнениями, это размещение a 2 и b 2 . a 2 всегда идет с переменной, ось которой параллельна более широкому направлению эллипса; b 2 всегда идет с переменной, ось которой параллельна более узкому направлению. Глядя на уравнения с другой стороны, больший знаменатель всегда дает значение a 2 , меньший знаменатель всегда дает значение b 2 , а два знаменателя вместе позволяют вам найти значение c 2 и ориентацию эллипса. Эллипсы по своей природе не являются «идеально круглыми» в том техническом смысле, в котором круги круглые, и мера величины, на которую эллипс «сжимается» от идеальной круглой формы, называется «эксцентриситетом» эллипса e «. Поскольку фокусы ближе к центру, чем вершины, то c < a , поэтому значение e всегда будет меньше 1. Если фокусы эллипса сдвинуты внутрь к центру, эллипс будет постепенно приближаться к окружности. Продолжая этот процесс, если мы допустим c = 0 (так что фокусы фактически находятся в центре), это будет соответствовать e = 0, а эллипс на самом деле будет окружностью. Это говорит нам о том, что значение e для истинного (некруглого) эллипса всегда будет больше 0. Сложив это вместе, мы видим, что 0 < e < 1 для любого эллипса. Когда ученые говорят о чем-то (например, о Плутоне) как об «эксцентрической» орбите, они не имеют в виду, что эта орбита причудливая или странная; они означают, что это «не круговое». (В случае Плутона его орбита время от времени фактически пересекает орбиту Нептуна.) Чем больше значение e , тем больше «сжимается» эллипс. Физическое свойство эллипсов заключается в том, что звуковые или световые лучи, исходящие из одного фокуса, будут отражаться обратно в другой фокус. Это свойство можно использовать, например, в медицине. Пациента, страдающего, скажем, камнями в желчном пузыре, можно поместить рядом с аппаратом, излучающим ударные волны от пациента в эллиптическую чашу. Пациента аккуратно укладывают так, чтобы камни в желчном пузыре находились в одном из фокусов эллипса, а между аппаратом и пациентом была проложена заполненная водой подушка, обеспечивающая эффективную передачу ударных волн. Машина излучает волны из другого фокуса эллипса; эти волны безвредно рассеиваются от излучателя в эллиптическую чашу, отражаются от чаши и, наконец, повторно концентрируются в другом фокусе (внутри пациента). Ударные волны достигают полной мощности только в очаге у пациента, где они разбивают камень на достаточно мелкие кусочки, чтобы организм пациента мог избавиться от них самостоятельно. URL: https://www.purplemath.com/modules/ellipse.htm Страница 2Страница 3Страница 4 Коническое сечение, или коническое , представляет собой форму, полученную в результате пересечения прямого кругового конуса с плоскостью. Угол, под которым плоскость пересекает конус, определяет форму. Конические сечения также могут быть описаны набором точек на координатной плоскости. Далее в этой главе мы увидим, что график любого квадратного уравнения с двумя переменными представляет собой коническое сечение. Знаки уравнений и коэффициенты переменных членов определяют форму. Мы можем нарисовать эллипс, используя кусок картона, две кнопки, карандаш и нитку. Поместите кнопки в картон, чтобы сформировать фокусы эллипса. Отрежьте кусок веревки длиннее, чем расстояние между двумя кнопками (длина веревки представляет собой константу в определении). Прикрепите каждый конец веревки к картону и начертите кривую карандашом, натянутым на веревку. В результате получается эллипс. Каждый эллипс имеет две оси симметрии. Более длинная ось называется большой осью , а более короткая ось называется малой осью . Каждая конечная точка большой оси является 90 205 вершиной 90 206 эллипса (множественное число: 90 205 вершин 90 206), а каждая конечная точка малой оси является 90 205 ко-вершиной 90 206 эллипса. В этом разделе мы ограничиваем эллипсы теми, которые расположены вертикально или горизонтально в координатной плоскости. То есть оси будут лежать или быть параллельными осям x и y . Позже в этой главе мы увидим эллипсы, вращающиеся в координатной плоскости. Для работы с горизонтальными и вертикальными эллипсами в координатной плоскости мы рассмотрим два случая: те, которые центрированы в начале координат, и те, которые центрированы в точке, отличной от начала координат. Сначала мы научимся выводить уравнения эллипсов, а потом научимся записывать уравнения эллипсов в стандартной форме. Позже мы будем использовать полученные знания для построения графиков. Чтобы вывести уравнение эллипса с центром в начале координат, мы начнем с фокусов [латекс](-c,0)[/латекс] и [латекс](с,0)[/латекс]. Если [латекс](а,0)[/латекс] является вершиной эллипса, расстояние от [латекс](-c,0)[/латекс] до [латекс](а,0)[/латекс ] представляет собой [латекс]а-(-с)=а+с[/латекс]. Расстояние от [латекс](с,0)[/латекс] до [латекс](а,0)[/латекс] равно [латекс]а-с[/латекс]. Сумма расстояний от фокусов до вершины равна [латекс](а+с)+(а-с)=2а[/латекс] Если [латекс](х,у)[/латекс] является точкой на эллипсе, то мы можем определить следующие переменные: [латекс]\begin{align}d_1&=\text{расстояние от } (-c,0) \text{ до } (x,y) \\ d_2&= \text{расстояние от } (c,0 ) \text{ to } (x,y) \end{align}[/latex] По определению эллипса [latex]d_1+d_2[/latex] является константой для любой точки [latex](x, y)[/latex] на эллипсе. Мы знаем, что сумма этих расстояний равна [latex]2a[/latex] для вершины [latex](a,0)[/latex]. для эллипса с центром в начале координат, большая ось которого лежит на оси Y . Стандартные формы уравнений рассказывают нам об основных характеристиках графиков. Найдите минутку, чтобы вспомнить некоторые стандартные формы уравнений, с которыми мы работали в прошлом: линейные, квадратичные, кубические, экспоненциальные, логарифмические и так далее. Научившись интерпретировать стандартные формы уравнений, мы наводим мосты между алгебраическими и геометрическими представлениями математических явлений. Ключевыми характеристиками эллипса являются его центр, вершины, ко-вершины, фокусы, а также длины и положения большой и малой осей. Как и в случае с другими уравнениями, мы можем определить все эти функции, просто взглянув на стандартную форму уравнения. Рисунок: (а) горизонтальный эллипс с центром (0,0), (б) вертикальным эллипсом с центром (0,0) Какое уравнение стандартной формы представляет собой эллипс с вершинами [латекс](\pm 8,0)[/латекс] и фокусами [латекс] (\pm 5,0)[/латекс]? Показать Показать решение Уравнение стандартной формы эллипса с вершинами [латекс]\влево(0,\pm 8\право)[/латекс] и фокусами [латекс](0,\pm \sqrt{5 })[/латекс]? Показать решение Как и графики других уравнений, график эллипса можно перевести. (a) Горизонтальный эллипс с центром [латекс]\левый(h,k\правый)[/латекс] (b) Вертикальный эллипс с центром [латекс]\левый(ч,к\правый)[/латекс] Уравнение стандартной формы эллипса с вершинами [латекс]\влево(-2,-8\вправо)[/латекс] и [латекс]\влево(-2,\текст{2}\вправо)[/латекс] и фокусы [латекс]\влево(-2,-7\вправо)[/латекс] и [латекс]\влево(- 2,\text{1}\right)?[/latex] Показать решение Уравнение стандартной формы эллипса с вершинами [латекс]\влево(-3,3\вправо)[/латекс] и [латекс]\влево(5,3\вправо)[/ латекс] и фокусы [латекс]\влево(1 — 2\sqrt{3},3\вправо)[/латекс] и [латекс]\влево(1+2\sqrt{3},3\вправо)?[/ латекс] Показать решение Многие ситуации реального мира могут быть представлены эллипсами, включая орбиты планет, спутников, лун и комет, а также формы килей лодок, рулей и некоторых крыльев самолетов. Скульптурный зал в здании Капитолия в Вашингтоне, округ Колумбия, представляет собой комнату для шепота. Его размеры составляют 46 футов в ширину и 96 футов в длину. а. Какова стандартная форма уравнения эллипса, представляющего контур комнаты? Подсказка: предположим, что это горизонтальный эллипс, и пусть центром комнаты будет точка [латекс]\влево(0,0\вправо)[/латекс]. б. Если два сенатора, стоящие в фокусах этой комнаты, слышат шепот друг друга, как далеко друг от друга находятся сенаторы? Округлить до ближайшего фута. Показать решение Предположим, комната для шепота имеет длину 480 футов и ширину 320 футов. а. Какова стандартная форма уравнения эллипса, представляющего комнату? Подсказка: предположим, что это горизонтальный эллипс, и пусть центром комнаты будет точка [латекс]\влево(0,0\вправо)[/латекс]. б. Если два человека стоят в фокусах этой комнаты и слышат шепот друг друга, как далеко друг от друга находятся люди? Округлить до ближайшего фута. Показать решение У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад. Улучшить эту страницуПодробнее Открытый справочник по математике Главная
Контакт
О
Тематический указатель Кривая линия, образующая замкнутый контур, где сумма расстояний от двух точек (фокусов) до каждой точки на линии постоянна. Попробуйте это Перетащите любую оранжевую точку. Вы можете изменить положение двух точек фокусировки (F1, F2).
Также перетащите точку на эллипс и обратите внимание, что сумма длин пересекающихся линий постоянна. Эллипс выглядит как круг, сжатый в овал. Как и круг, эллипс является типом линии. Представьте себе прямую
отрезок линии, изогнутый до тех пор, пока его концы не соединятся.
Затем сформируйте эту петлю, пока она не станет эллипсом — своего рода «сжатым кругом», как показано выше.
Вещи, имеющие форму эллипса, называются «эллиптическими». Эллипс определяется двумя точками, каждая из которых называется фокусом. (F1, F2 выше).
Если взять любую точку эллипса, сумма расстояний до точек фокусировки будет постоянной.
На рисунке выше перетащите точку на эллипсе и увидите, что
в то время как расстояния до точек фокусировки меняются, их сумма постоянна.
Размер эллипса определяется суммой этих двух расстояний. Две линии a и b , которые определяют эллипс, называются
линии генератора. Каждый из них иногда называют
образующая. Положение фокусов (множественное число от фокуса, произносится как «вздох врага») определяет, насколько «сплющен» эллипс.
Перетащите F1 и F2 и посмотрите, как это происходит.
Если они находятся в одном месте, эллипс представляет собой круг. Круг, по сути, является частным случаем эллипса.
На рисунке выше перетащите один фокус, пока он не окажется над другим.

Что такое «эксцентриситет» эллипса?
 Значение эксцентриситета эллипса определяется как e = c / a .
Значение эксцентриситета эллипса определяется как e = c / a .
Какое физическое свойство эллипсов?
 Пациент может вернуться домой в тот же день, так как он не подвергался хирургическому вмешательству.
Пациент может вернуться домой в тот же день, так как он не подвергался хирургическому вмешательству. Уравнения эллипсов | Колледж Алгебра
Результаты обучения
 В этом разделе основное внимание уделяется четырем вариантам стандартной формы уравнения эллипса. Эллипс — это множество всех точек [латекс]\влево(х,у\вправо)[/латекс] на плоскости, сумма расстояний от которых до двух фиксированных точек является константой. Каждая фиксированная точка называется фокус (множественное число: фокусы ) эллипса.
В этом разделе основное внимание уделяется четырем вариантам стандартной формы уравнения эллипса. Эллипс — это множество всех точек [латекс]\влево(х,у\вправо)[/латекс] на плоскости, сумма расстояний от которых до двух фиксированных точек является константой. Каждая фиксированная точка называется фокус (множественное число: фокусы ) эллипса. Центр эллипса является серединой большой и малой осей. Оси перпендикулярны в центре. Фокусы всегда лежат на большой оси, и сумма расстояний от фокусов до любой точки эллипса (постоянная сумма) больше, чем расстояние между фокусами.
Центр эллипса является серединой большой и малой осей. Оси перпендикулярны в центре. Фокусы всегда лежат на большой оси, и сумма расстояний от фокусов до любой точки эллипса (постоянная сумма) больше, чем расстояние между фокусами.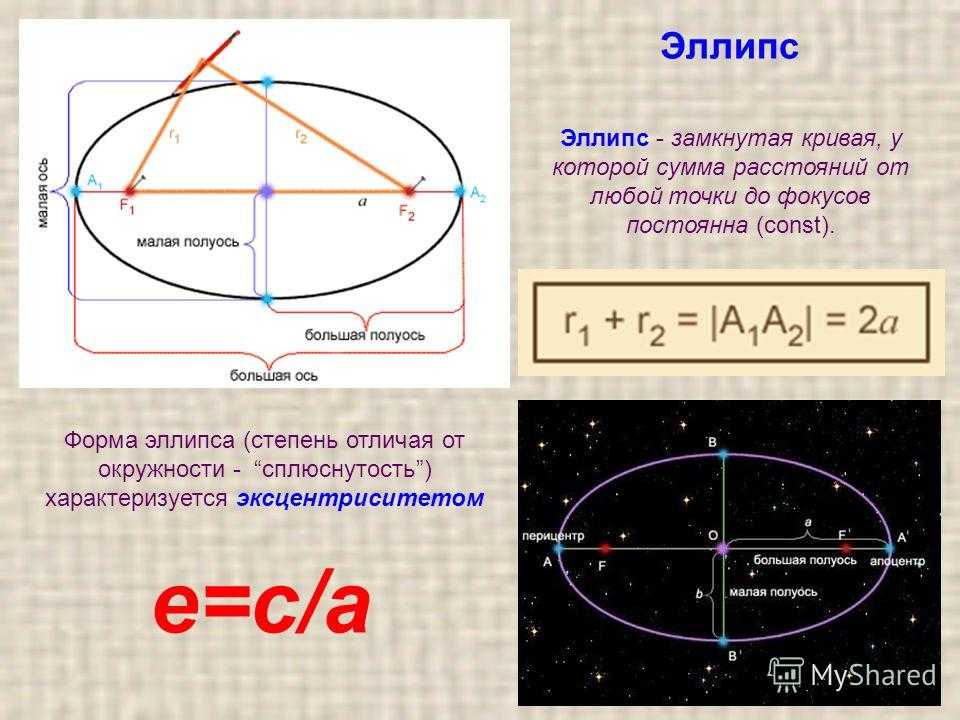 Эллипс — это множество всех точек [латекс](х,у)[/латекс], для которых сумма расстояний от [латекс](х,у)[/латекс] до фокусов постоянна, как показано на рисунок ниже.
Эллипс — это множество всех точек [латекс](х,у)[/латекс], для которых сумма расстояний от [латекс](х,у)[/латекс] до фокусов постоянна, как показано на рисунок ниже. Отсюда следует, что [latex]d_1+d_2=2a[/latex] для любой точки эллипса. Вывод стандартной формы уравнения эллипса основан на этом соотношении и формуле расстояния. Вывод выходит за рамки этого курса, но уравнение: 92}=1[/latex]
Отсюда следует, что [latex]d_1+d_2=2a[/latex] для любой точки эллипса. Вывод стандартной формы уравнения эллипса основан на этом соотношении и формуле расстояния. Вывод выходит за рамки этого курса, но уравнение: 92}=1[/latex] Написание уравнений эллипсов с центром в начале координат в стандартной форме
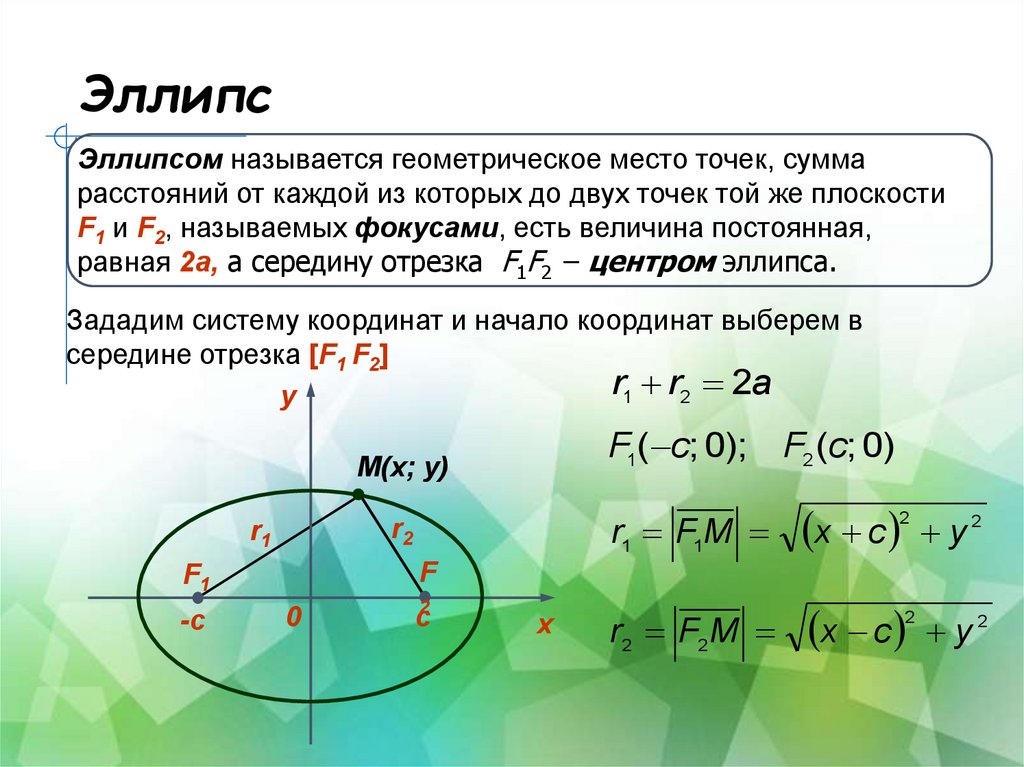 Существует четыре варианта стандартной формы эллипса. Эти вариации классифицируются сначала по местоположению центра (начало или не начало), а затем по положению (горизонтальное или вертикальное). Каждый представлен вместе с описанием того, как части уравнения соотносятся с графиком. Интерпретация этих частей позволяет нам сформировать ментальную картину эллипса. 92[/латекс]. Когда нам даны координаты фокусов и вершин эллипса, мы можем использовать соотношение, чтобы найти уравнение эллипса в стандартной форме.
Существует четыре варианта стандартной формы эллипса. Эти вариации классифицируются сначала по местоположению центра (начало или не начало), а затем по положению (горизонтальное или вертикальное). Каждый представлен вместе с описанием того, как части уравнения соотносятся с графиком. Интерпретация этих частей позволяет нам сформировать ментальную картину эллипса. 92[/латекс]. Когда нам даны координаты фокусов и вершин эллипса, мы можем использовать соотношение, чтобы найти уравнение эллипса в стандартной форме. Как: Учитывая вершины и фокусы эллипса, центрированного на происхождении, написать его уравнение в стандартной форме.
Пример: запись уравнения эллипса с центром в начале координат в стандартной форме
попробуйте
Написание уравнений эллипсов, не центрированных в начале координат
 Если эллипс переместить [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр эллипса будет [latex]\left(h,k\right)[/latex] . Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [латекс]х[/латекс] на [латекс]\влево(хч\вправо)[/латекс] и 9{2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти уравнение эллипса в стандартной форме, когда заданы вершины и фокусы.
Если эллипс переместить [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр эллипса будет [latex]\left(h,k\right)[/latex] . Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [латекс]х[/латекс] на [латекс]\влево(хч\вправо)[/латекс] и 9{2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти уравнение эллипса в стандартной форме, когда заданы вершины и фокусы. Как: Учитывая вершины и фокусы эллипса, не центрированные в начале координат, напишите его уравнение в стандартной форме.
Пример: Написание уравнения эллипса с центром в точке, отличной от начала координат
Попробуйте
Решение прикладных задач, связанных с эллипсами
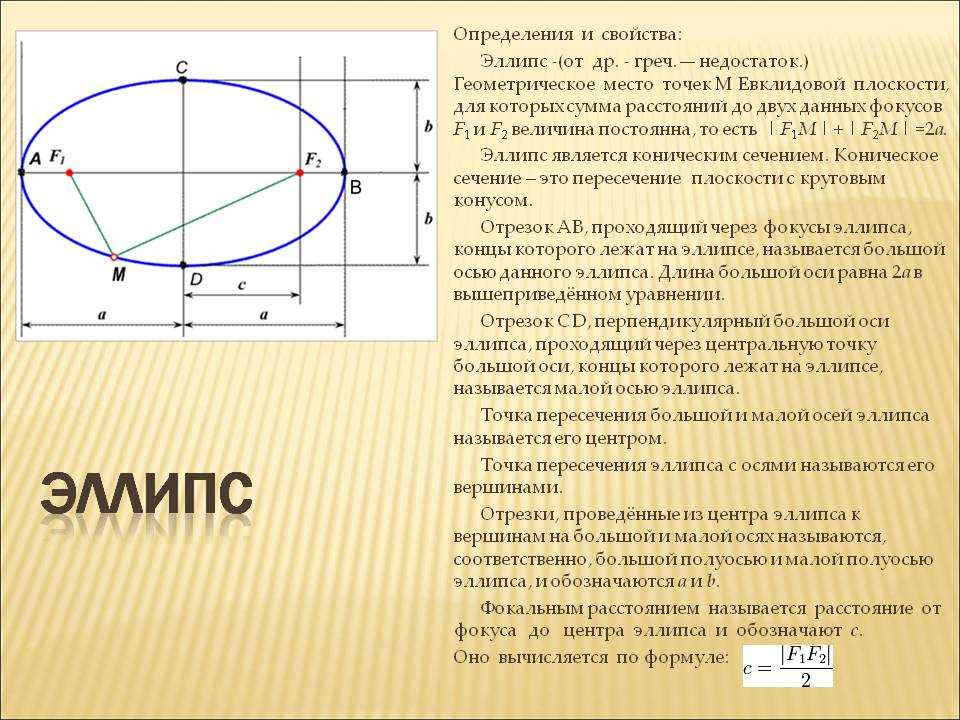 Медицинское устройство под названием литотриптер использует эллиптические отражатели для разрушения камней в почках путем создания звуковых волн. Некоторые здания, называемые камерами шепота, спроектированы с эллиптическими куполами, так что человек, шепчущий в одном фокусе, может быть легко услышан кем-то, стоящим в другом фокусе. Это происходит из-за акустических свойств эллипса. Когда звуковая волна возникает в одном фокусе шепчущей камеры, звуковая волна будет отражаться от эллиптического купола и обратно в другой фокус. В комнате для шепота в Музее науки и промышленности в Чикаго два человека, стоящие в фокусах на расстоянии около 43 футов друг от друга, могут слышать шепот друг друга.
Медицинское устройство под названием литотриптер использует эллиптические отражатели для разрушения камней в почках путем создания звуковых волн. Некоторые здания, называемые камерами шепота, спроектированы с эллиптическими куполами, так что человек, шепчущий в одном фокусе, может быть легко услышан кем-то, стоящим в другом фокусе. Это происходит из-за акустических свойств эллипса. Когда звуковая волна возникает в одном фокусе шепчущей камеры, звуковая волна будет отражаться от эллиптического купола и обратно в другой фокус. В комнате для шепота в Музее науки и промышленности в Чикаго два человека, стоящие в фокусах на расстоянии около 43 футов друг от друга, могут слышать шепот друг друга. Пример: определение фокусов комнаты для шепота

Попробуйте
Внесите свой вклад!
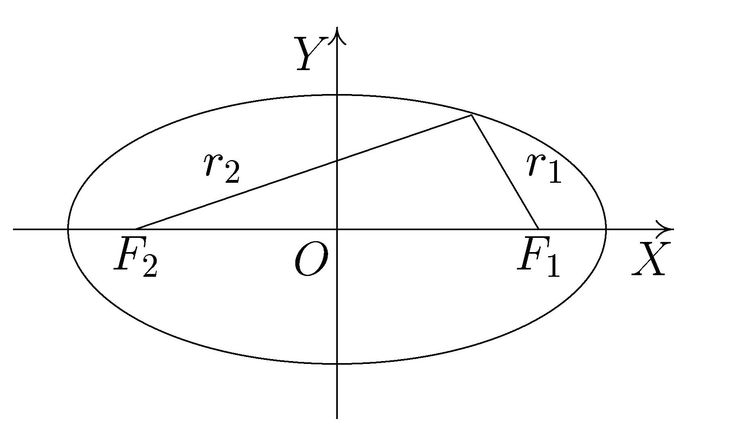
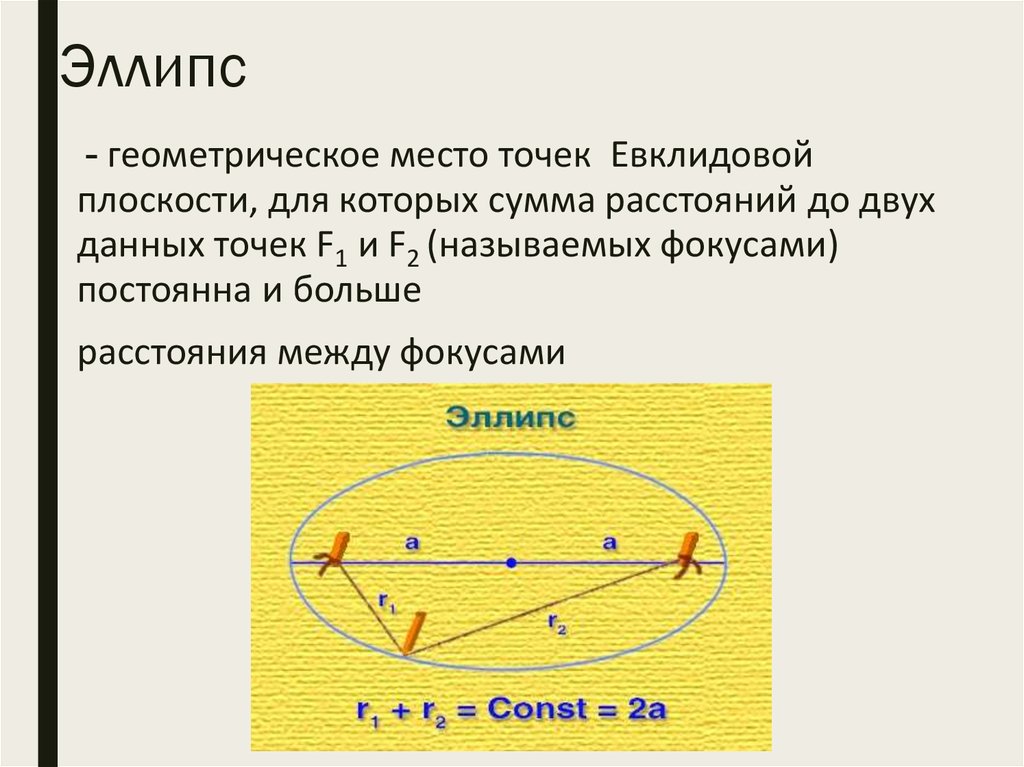
Как определяются эллипсы
 Сумма этих расстояний равна длине
большая ось (самый длинный диаметр эллипса).
Сумма этих расстояний равна длине
большая ось (самый длинный диаметр эллипса). Свойства эллипса
Центр Точка внутри эллипса, являющаяся серединой отрезка, соединяющего два фокуса.
Пересечение большой и малой осей. Большая/малая ось Самый длинный и самый короткий диаметры эллипса.  См. Большая / Малая ось эллипса.
Длина большой оси равна сумме двух
линии генератора (а и б на схеме выше).
См. Большая / Малая ось эллипса.
Длина большой оси равна сумме двух
линии генератора (а и б на схеме выше). Большая/малая полуось Расстояние от центра до самой дальней и ближайшей точки эллипса.
Половина большой/малой оси.
См. Большая полуось/малая полуось эллипса. Фокусы (точки фокусировки) Две точки, определяющие эллипс. См. Фокусы эллипса. Периметр (окружность) Периметр — это расстояние вокруг эллипса. Не легко вычислить.
См. Периметр эллипса. Зона Количество квадратных единиц, необходимое для заполнения области внутри эллипса.
См. Площадь, заключенная в эллипс. Хорд Отрезок, соединяющий любые две точки эллипса. 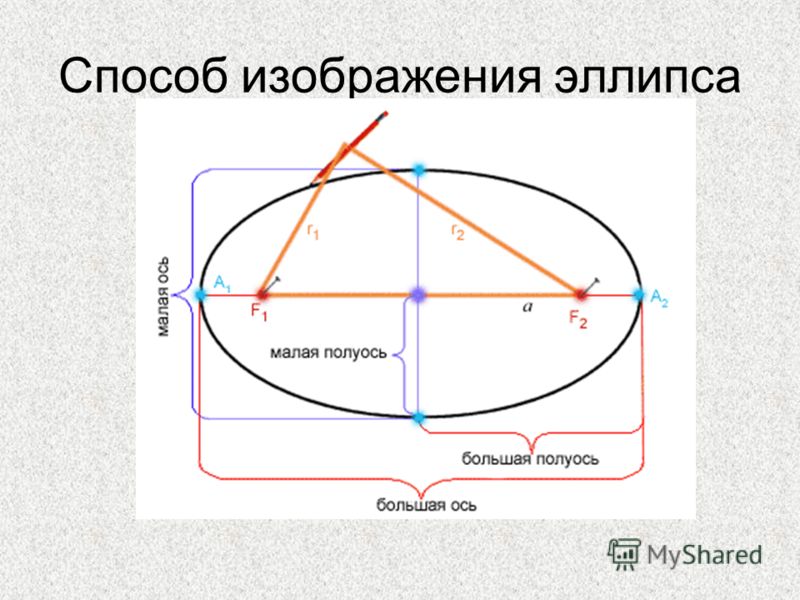
Тангенс Линия, проходящая через эллипс и касающаяся его только в одной точке.
См. Тангенс к эллипсу Секущая Прямая, пересекающая эллипс в двух точках. Отношение к окружности
На самом деле круг — это частный случай эллипса.
В эллипсе, если вы сделаете большую и малую оси одинаковой длины, в результате получится круг с обоими фокусами в центре.
См. определение круга Как нарисовать эллипс
Есть несколько практических способов нарисовать эллипс заданного размера.
См. Рисование эллипса с помощью веревки и булавок. Другие определения эллипса
Существуют и другие способы определения эллипса, которые используют
координатная геометрия:
t параметр
a — горизонтальная полуось и
b вертикальная полуось.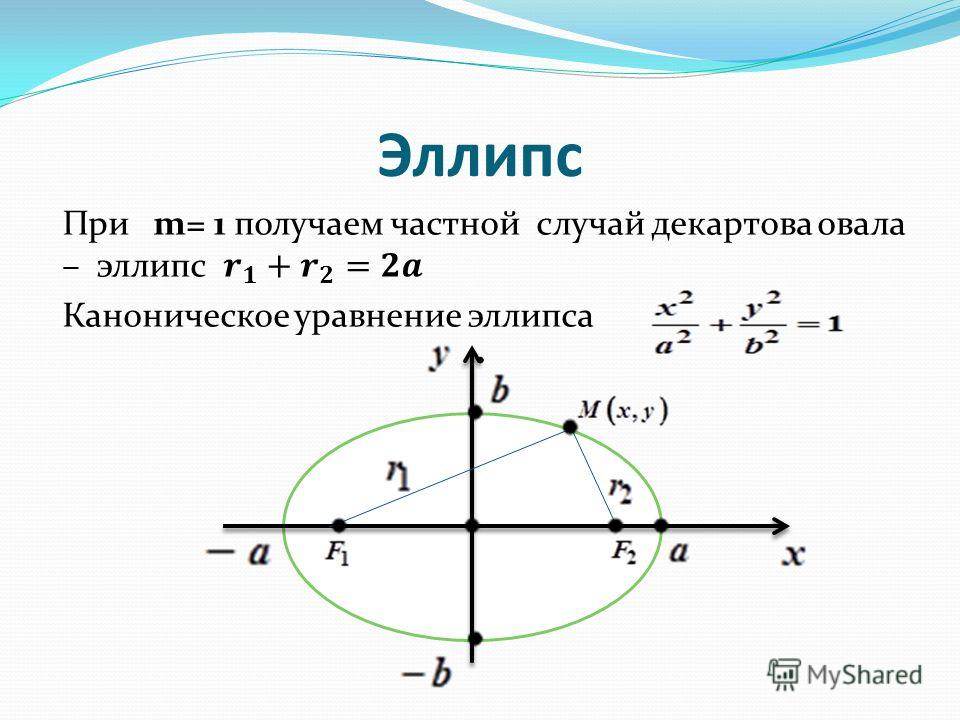
 Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.