Чем полезен тренажер эллипс?
Эллипс представляет собой универсальный тренажер для аэробных тренировок. Данный вид спортивного оборудования подходит как для восстановления физической формы спортсменов, так и для новичков в кардионагрузках. Плавные движения минимизируют возможность получения растяжений и травм, а естественная амплитуда кручения педалей способствует интуитивной эксплуатации, не требует помощи и присутствия специалиста.
Рассмотрим основные полезные свойства тренировок на эллиптическом тренажере. Прежде всего, это повышение общего мышечного тонуса. Конструкция тренажера позволяет имитировать 4 вида активных движений от лыжного спорта до подъема вверх по лестнице, в результате чего одновременно работают верхняя и нижняя группа мышц. В процессе тренировки задействуются задняя поверхность бедер, ягодицы, мышцы голени, дельтовидная группы мышц спины, а также пресс и плечевой пояс. Функция обратного хода позволяет акцентировать внимание на труднодоступных местах, укрепляет икроножные мышцы и подколенные сухожилия.
Главное преимущество тренажера заключается в том, что в процессе тренировки нагрузка на организм распределяется равномерно по всему телу, что не только снижает влияние на позвоночник и суставы, но и помогает избежать усталости и перенапряжения. Тренажер корректирует спортивный силуэт и исправляет проблемные зоны, не перекачивая мышцы на ногах, что симпатизирует женской аудитории и делает эллипс лидером для домашних тренировок.
Эллипс: снижение веса, сохранение баланса тела и улучшение кровообращения
Главный бонус спортивного оборудования – это эффективное снижение веса. Эллипс рекомендуют при равномерном похудении. В процессе тренировки, напряжение бедер и ягодиц способствует разогреву всего тела, что повышает расщепление жиров в проблемных зонах. По статистике, в течение 30 минут занятий на эллиптическом тренажере можно сжечь от 150 до 400 калорий. Результат будет зависеть от интенсивности движений, положения тела на орбитреке и типа «хода».
Так же, стоит отметить повышение координации и подвижности организма. Синхронизация движений рук и ног позволяет улучшить мобильность тела, и укрепляет связь между мозгом и конечностями.
Эллиптический тренажер способствует укреплению сердечно-сосудистой системы. Организм эффективно насыщается кислородом, что повышает частоту сердечных сокращений и укрепляет миокард. Регулярные тренировки увеличивают сердечную емкость, что улучшает кровообращение. Хороший кровоток не только способствует общему повышению иммунитета и снижает риск возникновения хронических заболеваний, но и улучшает качество сна, состояние кожи и волос.
Эллипс — уникальный тренажер, который помогает укрепить общий тонус организма и скорректировать проблемные зоны тела, в зависимости от вариативности позы, типа «хода» и интенсивности режима. Регулярные тренировки на орбитреке положительно сказываются на здоровье человека:
· Укрепляют мышечный корсет и повышают выносливость организма;
· Эффективно содействуют в снижении веса и энергообменных процессах;
· Положительно сказываются на дыхательной, сердечной и сосудистой системах организма.
Идеальное решение для реабилитации
Возникновение травм, особенно серьезных, способно оказать сильное влияние на карьеру спортсмена. Тем более всегда требуется правильное возвращение в мир спорта, верное и мягкое восстановление работы мышц. Если сделать что-то не так или перенапрячься, то можно лишь усилить травму или же создать совершенно новую.
Эллиптический тренажер является отличным помощником для спортсменов, проходящих период реабилитации. Ключевым его преимуществом является способность охватывать большую зону проблем, оказывая на организм благоприятное воздействие. Помимо указанного ранее влияния на сердечно-сосудистую систему, можно отметить заметное улучшение аэробных способностей организма пользователя.
Самое важное – останавливается процесс деградации или атрофирования мускулатуры – это именно то, что так опасно во время травм, спортсмен может потерять большой объем мышц, из-за чего возвращение в большой спорт станет невозможным или слишком затянется. Важно и то, что эллипс не дает ударную нагрузку на позвоночный столб, а также не оказывает пагубное влияние на суставы: коленные, голеностопные и тазобедренные). С помощью данного тренажера спортсмен может имитировать различную спортивную деятельность, начиная с обычной прогулочной ходьбы и заканчивая подъемом в гору или же быстрым передвижением на лыжах.
Важно и то, что эллипс не дает ударную нагрузку на позвоночный столб, а также не оказывает пагубное влияние на суставы: коленные, голеностопные и тазобедренные). С помощью данного тренажера спортсмен может имитировать различную спортивную деятельность, начиная с обычной прогулочной ходьбы и заканчивая подъемом в гору или же быстрым передвижением на лыжах.
В каких случаях проблем со здоровьем используется эллипс?
Начнем именно с возможности эллипса положительно влиять на кровообращение. Такие заболевания, как артрит, остеохондроз, артроз или защемление нерва, возникают как раз в виду недостаточного кровообращения. Малоподвижный образ жизни аналогичным образом может пагубно сказаться на здоровье в виде отложений соли. Именно по этой причине для лечения указанных заболеваний активно используется эллиптический тренажер – он даст нагрузку сразу на все тело, при этом не будет пагубно влиять на суставы.
При переломах суставов (голеностопного и тазобедренного) часто в качестве реабилитации назначается эллипс, кстати, при повреждениях позвоночника также назначают именно его. Причина тому — способность воздействовать на мускулатуру, минуя нагрузку на суставы и позвоночник.
Причина тому — способность воздействовать на мускулатуру, минуя нагрузку на суставы и позвоночник.
Для женщин, у которых прошли тяжелые роды или же проводилась операция на органах малого таза также будет полезен именно эллипс. Спортсменка сможет поддерживать мышцы в тонусе, не перенапрягая те части тел, которым лишняя нагрузка в конкретный момент точно не нужна.
Fitness Place – территория здорового образа жизни. На нашем маркетплейс покупатель сможет подобрать свой эллиптический тренажер, который будет идеально подходить под его запросы и финансовые возможности.
Построение эллипсов. Как рисовать овалы?
- ВСЕ
- Рисование
- Советы художника
- История искусств
- Живопись
- Рисунок
- Цветоведение
- Поэтапное рисование
- Вдохновение
- О художниках
- Ученики
- Композиция
- Абстракция
- Книги
04. 10.2018 12:19
10.2018 12:19
Один из моих учителей на первом курсе училища даже выделял 16 видов неправильных эллипсов. Он долго рисовал их на доске и подробно объяснял, как рисовать не надо. Это было очень смешно. Я, конечно, не помню все 16, но некоторые из них со временем даже приобрели названия, которые мы с учениками с удовольствием используем на занятиях рисунком. Благодаря ассоциативным образам, теперь каждый начинающий художник может проверить свои эллипсы на ошибки. “Рыбка”, “огурчик”, “пирожок”, “сосиска”… Но чаще встречается квадрат со скруглёнными углами — всё это неточности и ошибки в построении.
А теперь давайте разбираться как нарисовать эллипс правильно и красиво.
1)Эллипс — это круг, лежащий в плоскости, поэтому выглядеть он должен именно так и никак иначе. Если ощущения округлой формы нет, значит где-то есть искажения, придётся править рисунок.
2) Эллипс касается направляющих, в которые он заключён, только четырьмя точками(верх, низ, право, лево) и ни в коем случае не может “прилипнуть” к линиям построения частью своей поверхности.
3) В зависимости от линии горизонта, раскрытие эллипсов разное. В рисунке это должно быть хорошо видно и логически осмысленно. Чем выше или ниже линия горизонта (чем дальше от неё удалён эллипс), тем раскрытие эллипса больше. На линии горизонта эллипс, как и любая другая плоскость, превращается в линию. Поэтому есть разница, с какой именно точки и высоты мы смотрим на объект: рисуем сидя или стоя. Помните, что линия горизонта всегда находится на уровне ваших глаз.
4) Эллипс — не овал, хотя и очень на него похож. Дело в том, что одна из половинок эллипса (ближайшая к нам часть круга) визуально крупнее, чем другая половина. Тут вступает в силу закон линейной перспективы: чем ближе к нам объекты, тем они крупнее. По мере удаления от зрителя, они выглядят более мелкими. Вспомните деревья вдоль аллеи: в глубине они кажутся более низкими, чем те, которые находятся непосредственно рядом с наблюдателем. С половинками эллипса всё то же самое, только это не так сильно заметно. Поэтому при построении эллипса, серединную горизонтальную линию следует расположить чуть выше середины, если линия горизонта над объектом и чуть ниже, если она под объектом таким образом передняя половинка эллипса в рисунке станет выглядеть немного крупнее дальней.
Тут вступает в силу закон линейной перспективы: чем ближе к нам объекты, тем они крупнее. По мере удаления от зрителя, они выглядят более мелкими. Вспомните деревья вдоль аллеи: в глубине они кажутся более низкими, чем те, которые находятся непосредственно рядом с наблюдателем. С половинками эллипса всё то же самое, только это не так сильно заметно. Поэтому при построении эллипса, серединную горизонтальную линию следует расположить чуть выше середины, если линия горизонта над объектом и чуть ниже, если она под объектом таким образом передняя половинка эллипса в рисунке станет выглядеть немного крупнее дальней.
5) Симметричные половинки — правая и левая. А вот правая и левая части эллипса всегда одинаковы. Постарайтесь избежать любого искажения или неровности в одной из половин — они зеркальное отражение друг друга.
6) Существуют разные варианты построения эллипса, расположенного на горизонтальной плоскости. На уроках рисунка с учениками в классе мы строим эллипсы просто и быстро, банально вписывая округлую форму в положенное ей место и ориентируемся по линиям “крестовины” для поддержания симметрии.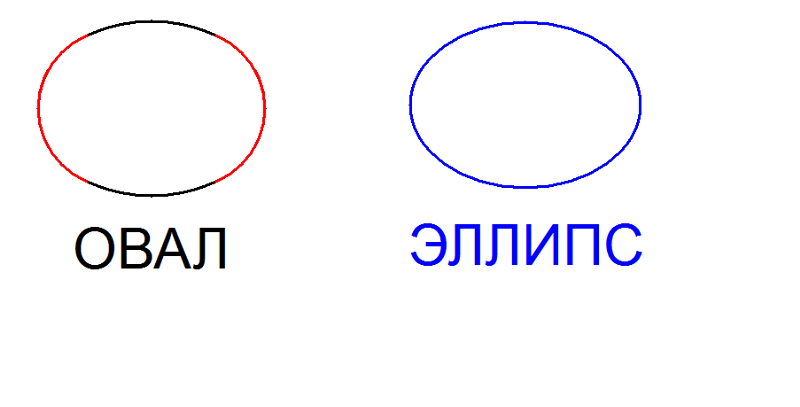 Чтобы визуально было проще представить раскрытие плоскости и сокращение её в глубину, можно наметить для себя условные боковые направляющие. Это даст ощущение пространства и чувство ухода плоскости в глубину от зрителя.
Чтобы визуально было проще представить раскрытие плоскости и сокращение её в глубину, можно наметить для себя условные боковые направляющие. Это даст ощущение пространства и чувство ухода плоскости в глубину от зрителя.
Ещё один вариант, помогающий соблюсти симметрию правой и левой частей эллипса наиболее точно и позволяющий доказать правильность расположения серединной горизонтальной линии — проведение диагоналей при построении. Выбирайте вариант на свой вкус.
7) После освоения построения эллипсов, лежащих в горизонтальной плоскости (наиболее часто встречающийся вариант), можно начинать строить эллипсы, находящиеся в вертикальном положении. Тут, чтобы не ошибиться, лучше выстраивать цилиндрическую форму от четырёхгранной коробки.
8) Также эллипсы могут находиться совершенно в любом положении в пространстве. Тут придётся включить логику и воображение и самостоятельно определить наклон плоскости, в которую вписан эллипс, её размер и положение в среде, нарисовать в ней все необходимые направляющие и выстроить эллипс как подобает. Постарайтесь максимально точно определить положение плоскости, тогда построение эллипса не доставит вам хлопот.
Постарайтесь максимально точно определить положение плоскости, тогда построение эллипса не доставит вам хлопот.
Вот такая, вроде бы, незатейливая теория, но требующая глубокого погружения и тщательного анализа. Надеюсь, что теперь с эллипсами у вас не будет ни малейших трудностей. Пусть рисование приносит вам удовольствие и самоудовлетворение. Удачи!
Если вам понравилась эта статья, сделайте следующее:
1. Поставьте «лайк».
2. Поделитесь этим постом с друзьями в социальных сетях или своём блоге.
3. Покупайте у нас курс «Рисование с нуля до портрета на заказ» в Екатеринбурге. 🙂
Эллипс Определение и значение | Dictionary.com
- Основные определения
- Тест
- Связанный контент
- Примеры
- Британский
- Научный
- Культурный
Уровень сложности этого слова показывается на основе уровня сложности.
[ ih-lips ]
/ ɪˈlɪps /
См. слово, которое чаще всего путают с эллипсом
Сохранить это слово!
См. синонимы для: эллипс / эллипсы на Thesaurus.com
Показывает уровень обучения в зависимости от сложности слова.
сущ. Геометрия.
плоская кривая такая, что суммы расстояний каждой точки на ее периферии от двух фиксированных точек, фокусов, равны. Это коническое сечение, образованное пересечением прямого круглого конуса плоскостью, пересекающей ось и поверхность конуса. Типичное уравнение: (x2/a2) + (y2/b2) = 1. Если a = b, эллипс представляет собой окружность.
СРАВНИТЬ ЗНАЧЕНИЯ
Нажмите, чтобы сравнить значения. Используйте функцию сравнения слов, чтобы узнать разницу между похожими и часто путаемыми словами.
ВИКТОРИНА
ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?
Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!
Удачи!
Вопрос 1 из 7
Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.
Происхождение эллипса
1745–55; <французский <латинское ellipsisellipsis; или обратным образованием из множественного числа эллипсов
Слова рядом с эллипсом
Эллис-Айлендс, Элликотт-Сити, Эллингтон, Эллингтон, Дьюк, Эллиотт, эллипс, эллипсис, эллипсограф, эллипсоид, эллипсоид, эллипсоид вращения
Dictionary.com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc. 2022
Слова, связанные со словом эллипс
дуга, арка, контур, петля, траектория, путь, узор, вращение, охват, изгиб, изгиб, изгиб, изгиб, цепная связь , хорда, круг, контур, окружность, компас, вогнутость
Как использовать эллипс в предложении
Миссии НАСА «Викинг» в 1970-х годах на Марс имели предполагаемый посадочный эллипс 280×100 км.
«7 минут ужаса»: технологическая настойчивость понадобится, чтобы выжить при посадке на Марс|Крис Джеймс|18 февраля 2021 г.
 |Singularity Hub
|Singularity Hub Это распространение, как обнаружил Ротермель, двигалось наружу тонким расширяющимся краем по эллипсу.
Что сложная математика моделирования пожаров говорит нам о будущем калифорнийских лесов|Эми Нордрам|18 января 2021|MIT Technology Review
Это что-то, согласно новому моделированию Несворни, скорее всего, это Нептун, который поскользнулся наружу по орбите именно такой формы, которая находится где-то между идеальным кругом и более сильно сплющенным эллипсом.
Ухабистое детство Нептуна может выявить недостающие планеты нашей Солнечной системы|Чарли Вуд|8 января 2021|Popular-Science
Эксцентриситет эллипса является мерой того, насколько он вытянут.
Мы космический 1 процент, но наша Солнечная система не совсем чудаковатая — настолько романтичные факты|Шон Рэймонд|5 января 2021 г.|Наутилус
Световой узор в вашем глазу, на сетчатке , конечно же, в форме эллипса.
Этот визуальный эксперимент разрешил многовековой философский спор — такие романтичные факты|Джим Дэвис|14 августа 2020 г.
 |Наутилус выглядеть так, как если бы компас проследил его.
|Наутилус выглядеть так, как если бы компас проследил его.Прочтите это и покраснейте: озорные средневековые французские сказки|Юнтэ Хуанг|13 июня 2013 г.|DAILY BEAST
18 декабря торжествующий Джонсон появился на Эллипсе возле Белого дома, чтобы зажечь национальную рождественскую елку.
Эпоха безумцев: Когда надежда была дешевой|Джонатан Дарман|19 марта 2012|DAILY BEAST
На орбите, ставшей эллиптической из-за планетарного притяжения, Солнце обязательно занимает один из фокусов эллипса.
Очерки истории Земли|Натаниэль Саутгейт Шалер
Более длинная ось эллипса сама находится в постоянном движении в том же направлении, в котором движется Земля.
Очерки истории Земли|Натаниэль Саутгейт Шалер
Форма представляет собой эллипс с осями 620 и 513 футов, здание занимает почти шесть акров земли.
Частная жизнь римлян|Гарольд Уэтстоун Джонстон
Теперь диск превратился в невероятно длинный эллипс, окруженный множеством меньших тел, фрагментов и содержимого корабля.

Greylorn|John Keith Laumer
Эллипс — это фигура, ограниченная непрерывной кривой, природа которой будет показана ниже.
Механический чертеж Самоучка|Джошуа Роуз
Определения слова эллипс в Британском словаре
эллипс
/ (ɪˈlɪps) /
существительное в форме наклонной конической плоскости
900 не пересекает основание конуса. Стандартное уравнение x ²/ a ² + y ²/ b ² = 1, где 2 a и 2 b — длины большой и малой осей. Площадь: π abПроисхождение слова для эллипса
C18: обратное образование из многоточия
Английский словарь Коллинза — полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения эллипса
эллипс
путем пересечения конуса плоскостью, не параллельной и не перпендикулярной основанию конуса. Сумма расстояний любой точки эллипса от двух фиксированных точек (называемых фокусами) остается постоянной независимо от того, где находится точка на кривой.
Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Культурные определения эллипса
эллипс
[ (i-lips) ]
) остается постоянным. Если фокусы идентичны друг другу, эллипс представляет собой круг; если два фокуса отличаются друг от друга, эллипс выглядит как сплющенный или вытянутый круг.
примечания для эллипса
Орбиты планет и многих комет представляют собой эллипсы.
Новый словарь культурной грамотности, третье издание Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Эллипсы
Эллипс в стандартной форме
ЭллипсНабор точек на плоскости, сумма расстояний которых от двух фиксированных точек равна положительной константе. это множество точек на плоскости, расстояния которых от двух фиксированных точек, называемых фокусами, имеют сумму, равную положительной постоянной. Другими словами, если точки F1 и F2 являются фокусами (множественное число от фокуса), а d — некоторая заданная положительная константа, то (x, y) — точка на эллипсе, если d=d1+d2, как показано ниже:
Другими словами, если точки F1 и F2 являются фокусами (множественное число от фокуса), а d — некоторая заданная положительная константа, то (x, y) — точка на эллипсе, если d=d1+d2, как показано ниже:
Кроме того, эллипс может быть образован пересечением конуса с наклонной плоскостью, которая не параллельна стороне конуса и не пересекает основание конуса. Точки на этом овале, где расстояние между ними максимально, называются вершинами эллипса, которые отмечают конечные точки большой оси. и определите большую ось. Сегмент линии, проходящий через центр эллипса, определяется двумя точками на эллипсе, где расстояние между ними максимально. Центр эллипса — это середина между вершинами. Малая ось Отрезок прямой, проходящий через центр эллипса, определяемый двумя точками на эллипсе, где расстояние между ними минимально. это отрезок, проходящий через центр эллипса, определяемый двумя точками на эллипсе, расстояние между которыми минимально. Конечные точки малой оси называются ко-вершинами. Точки на эллипсе, которые отмечают конечные точки малой оси..
Точки на эллипсе, которые отмечают конечные точки малой оси..
Если большая ось эллипса параллельна оси x в прямоугольной координатной плоскости, мы говорим, что эллипс горизонтален. Если большая ось параллельна оси y , мы говорим, что эллипс вертикальный. В этом разделе нас интересует только набросок этих двух типов эллипсов. Тем не менее, эллипс имеет много реальных применений, и поощряются дальнейшие исследования по этой богатой теме. В прямоугольной координатной плоскости, где центром горизонтального эллипса является (h,k), мы имеем
Как показано на рисунке a>b, где a , половина длины большой оси, называется большой радиус. Половина длины большой оси.. И b , половина длины малой оси, называется малым радиусом Половина длины малой оси.. Уравнение эллипса в стандартной формеУравнение эллипса, записанное в виде (x−h)2a2+(y−k)2b2= 1. Центр равен (h,k), и большее из a и b является большим радиусом, а меньшее — второстепенным радиусом.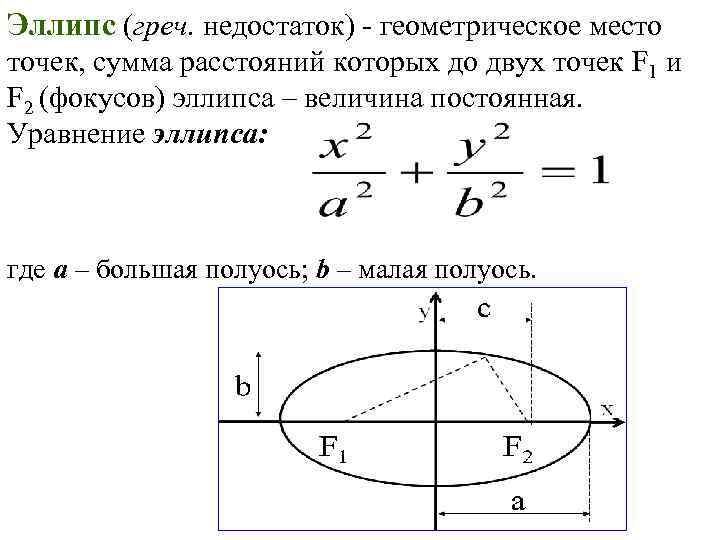 следует:
следует:
(x−h)2a2+(y−k)2b2=1
Вершины равны (h±a,k) и (h,k±b), а ориентация зависит от a и b . Если a>b, то эллипс горизонтален, как показано выше, а если a
График эллипса полностью определяется его центром, ориентацией, большим и малым радиусами, которые можно определить из его уравнения, записанного в стандартной форме.
Пример 1
График: (x+3)24+(y−2)225=1.
Решение:
Записав эту форму, мы увидим, что центр эллипса равен (−3,2), a=4=2 и b=25=5. От центральной отметки на 2 единицы влево и вправо и на 5 единиц вверх и вниз.
Затем нарисуйте эллипс через эти четыре точки.
Ответ:
Как и в случае любого графа, нас интересует нахождение точек пересечения x и y .
Пример 2
Найдите точки пересечения: (x+3)24+(y−2)225=1.
Решение:
Чтобы найти x -отрезков, установите y=0:
(x+3)24+(0−2)225=1(x+3)24+425=1(x+3 )24=1−425(x+3)24=2125
На этом этапе мы извлекаем корень, применяя свойство квадратного корня.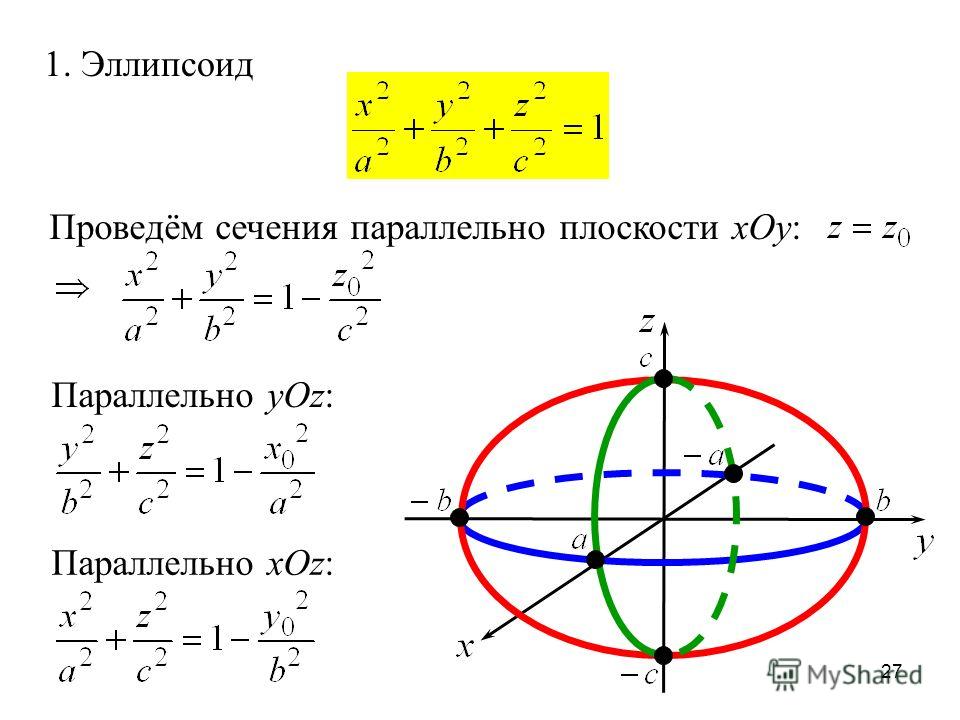
x+32=±2125x+3=±2215x=-3±2215=-15±2215
Полагая x=0 и находя y , мы получаем комплексные решения, поэтому y -отрезков не существует . Это оставлено в качестве упражнения.
Ответ: х — отрезки: (−15±2215,0); г -перехваты: нет.
В отличие от круга, стандартная форма эллипса требует 1 на одной стороне уравнения.
Пример 3
Постройте график и обозначьте точки пересечения: (x−2)2+9(y−1)2=9.
Решение:
Чтобы получить стандартную форму, с 1 в правой части, разделите обе части на 9.
(x−2)2+9(y−1)29=99(x−2)29+9 (y−1)29=99(x−2)29+(y−1)21=1
Следовательно, центр эллипса равен (2,1), a=9=3 и b=1=1. График выглядит следующим образом:
Чтобы найти точки пересечения, мы можем использовать стандартную форму (x−2)29+(y−1)2=1:
Следовательно, точка пересечения x равна (2,0) и y — точки пересечения равны (0,3+53) и (0,3−53).
Ответ:
Рассмотрим эллипс с центром в начале координат
x2+y24=1
Учитывая это уравнение, мы можем написать этой формы ясно, что центр равен (0,0), a=1 и b=2. Кроме того, если мы решим для y получаем две функции:
Кроме того, если мы решим для y получаем две функции:
x2+y24=1y24=1−x2y2=4(1−x2)y=±4(1−x2)y=±21−x2
Функция, определяемая y=21 −x2 — верхняя половина эллипса, а функция, определяемая формулой y=−21−x2, — нижняя половина.
Попробуйте! График: 9(x−3)2+4(y+2)2=36.
Ответ:
(щелкните, чтобы посмотреть видео)
Эллипс в общей форме
Мы видели, что график эллипса полностью определяется его центром, ориентацией, большим и малым радиусами; которое можно прочитать из его уравнения в стандартной форме. Однако уравнение не всегда дается в стандартной форме. Уравнение эллипса в общем видеУравнение эллипса записывается в виде px2+qy2+cx+dy+e=0, где p,q>0. следует,
px2+qy2+cx+dy+e=0 где р, q>0. Шаги построения графика эллипса по заданному уравнению в общем виде показаны в следующем примере.
Пример 4
График: 2×2+9y2+16x−90y+239=0.
Решение:
Начните с переписывания уравнения в стандартной форме.
Шаг 1: Сгруппируйте члены с одинаковыми переменными и переместите константу в правую сторону. Умножьте так, чтобы старший коэффициент каждой группы был равен 1,9.0019
2×2+9y2+16x−90y+239=0(2×2+16x+___)+(9y2−90y+___)=−2392(x2+8x+___)+9(y2−10y+___)=−239
Шаг 2: Заполните квадрат для каждой группы. В этом случае для терминов, включающих x , используйте (82)2=42=16, а для терминов, включающих y , используйте (−102)2=(−5)2=25. Коэффициент перед группировкой влияет на значение, используемое для балансировки уравнения в правой части:
2(x2+8x +16)+9(y2−10y+25)=−239 +32+225
Из-за свойства распределения добавление 16 внутри первой группы эквивалентно добавлению 2⋅16=32. Точно так же добавление 25 внутрь второй группы эквивалентно добавлению 9⋅25=225. Теперь размножьте, а затем разделите, чтобы получить 1 в правой части.

2(х+4)2+9(у-5)2=182(х+4)2+9(у-5)218=18182(х+4)218+9(у-5)218=1818 (х+4)29+(у-5)22=1
- Шаг 3: Определите центр, a и b . В этом случае центр равен (−4,5), a=9=3 и b=2.
- Шаг 4: Используйте a , чтобы отметить вершины слева и справа от центра, используйте b , чтобы отметить вершины вверх и вниз от центра, а затем нарисуйте график. В этом случае вершины вдоль малых осей (−4,5±2) не видны и должны быть помечены.
Ответ:
Пример 5
Определить центр эллипса, а также длины большой и малой осей: 5×2+y2−3x+40=0.
Решение:
В этом примере нам нужно заполнить квадрат только для условий, включающих x .
5×2+y2-30x+40=0(5×2-30x+___)+y2=-405(x2-6x+___)+y2=-40
Использование (-62)2=(-3)2= 9, чтобы первая группа была уравновешена 5⋅9=45 с правой стороны.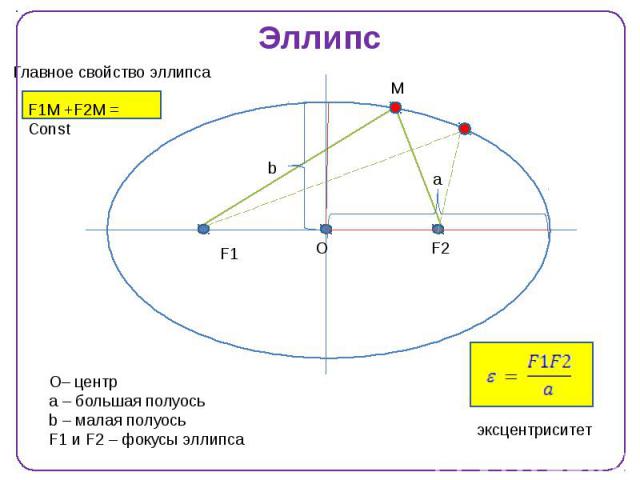
5(x2−6x +9)+y2=−40 +455(x−3)2+y2=55(x−3)2+y25=55(x−3)21+y25=1
Здесь центр равен (3,0), a=1=1 и b=5. Поскольку b больше, чем a , длина большой оси равна 2 b , а длина малой оси равна 2 a .
Ответ: Центр: (3,0); большая ось: 25 ед.; малая ось: 2 ед.
Попробуйте! График: x2+4y2+10x−16y+25=0.
Ответ:
(щелкните, чтобы посмотреть видео)
Ключевые выводы
- График эллипса полностью определяется его центром, ориентацией, большим и малым радиусами.
- Центр, ориентация, большой и малый радиус очевидны, если уравнение эллипса задано в стандартной форме: (x−h)2a2+(y−k)2b2=1.
- Чтобы нарисовать эллипс, отметьте точки a единиц слева и справа от центра и точки b единиц вверх и вниз от центра. Через эти точки начертите эллипс.
- Ориентация эллипса определяется a и b .
 Если a>b, то эллипс в ширину больше, чем в высоту и считается горизонтальным эллипсом. Если a
Если a>b, то эллипс в ширину больше, чем в высоту и считается горизонтальным эллипсом. Если a- Если уравнение эллипса задано в общем виде px2+qy2+cx+dy+e=0, где p,q>0, сгруппируйте члены с одинаковыми переменными и заполните квадрат для обеих групп.
- Мы распознаем уравнение эллипса, если оно квадратично как по x , так и по y и коэффициенты каждого квадратного члена имеют одинаковый знак.
Тематические упражнения
(х-1)24+(у+2)249=1
(х+3)264+(у-2)29=1
х23+(у+9)2=1
(x−1)28+y2=1
4(х+5)2+9(у+5)2=36
16(х-1)2+3(у+10)2=48
Центр (3,4) с a=5 и b=2.
Центр (−1,9) с a=7 и b=3.
Центр (5,−1) с a=6 и b=23.
Центр (−7,−2) с a=52 и b=7.
Центр (0,−3) с a=1 и b=5.
Центр (0,0) с a=2 и b=4.
(х-4)24+(у+2)29=1
(х+1)225+(у-2)24=1
(х-5)216+(у+6)21=1
(х+4)24+(у+3)236=1
(х-2)29+(у-1)264=1
(х+1)249+(у+3)2=1
4(х+3)2+9(у-3)2=36
16×2+(y−1)2=16
4(x−2)2+25y2=100
81×2+y2=81
(х-2)28+(у-4)29=1
(х+1)24+(у-1)212=1
(х-6)22+(у+2)25=1
(х+3)218+(у-5)23=1
3×2+2(y−3)2=6
5(х+1)2+3у2=15
4×2+6y2=24
5×2+10y2=50
(х-3)24+(у-2)29=1
(х+3)216+(у-7)29=1
(х-2)24+(у+6)236=1
(х+1)225+(у-1)29=1
5×2+2(y−4)2=20
4(x−3)2+9y2=72
5×2+2y2=10
3×2+4y2=24
Эллипс с вершинами (±5,0) и (0,±6).

Эллипс, большая ось которого имеет вершины (2,9) и (2,−1), а малая ось имеет вершины (−2,4) и (6,4).
Эллипс, большая ось которого имеет вершины (-8,-2) и (0,-2), а малая ось имеет длину 4 единицы.
Эллипс, большая ось которого имеет вершины (-2,2) и (-2,8), а малая ось имеет длину 2 единицы.
Часть A: Эллипс в стандартной форме
Имея уравнение эллипса в стандартной форме, определите его центр, ориентацию, большой и малый радиусы.
Определите стандартную форму уравнения эллипса, учитывая следующую информацию.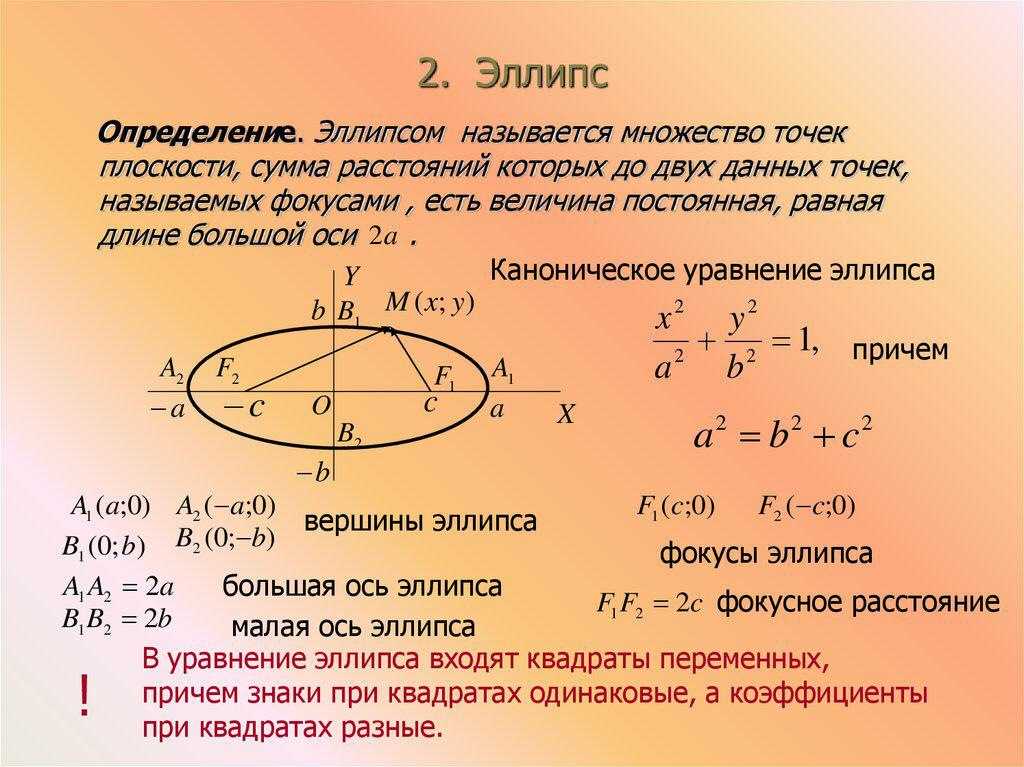
График.
Найдите точки пересечения x и y .
Найдите уравнение эллипса.
4×2+9y2+8x−36y+4=0
9×2+25y2-18x+100y-116=0
4×2+49y2+24x+98y-111=0
9×2+4y2-72x+24y+144=0
х2+64у2-12х+128у+36=0
16×2+y2-96x-4y+132=0
36×2+4y2-40y-44=0
х2+9у2-2х-8=0
х2+9у2-4х-36у-41=0
16×2+y2+160x−10y+361=0
4×2+5y2+32x−20y+64=0
2×2+3y2-8x-30y+65=0
8×2+5y2-16x+10y-27=0
7×2+2y2+28x−16y+46=0
36×2+16y2-36x-32y-119=0
16×2+100y2+64x−300y−111=0
х2+4у2-20у+21=0
9×2+y2+12x−2y−4=0
5×2+4y2-20x+24y+36=0
4×2+3y2-8x+6y-5=0
6×2+y2−12x+4y+4=0
8×2+y2-6y-7=0
5×2+2y2-20x-8y+18=0
2×2+3y2-4x-5y+1=0
(х-10)225+(у+3)25=1
(х+1)218+у236=1
7×2+3y2-14x+36y+94=0
4×2+8y2+20x−8y+11=0
Часть B: Эллипс в общей форме
Переписать в стандартной форме и графике.
По заданной общей форме определите пересечения.
Определить площадь эллипса. (Площадь эллипса находится по формуле A=πab, где a и b — длины большого и малого радиусов.)
По графику эллипса определите его уравнение в общем виде.
Объясните, почему круг можно рассматривать как особый эллипс.
Составьте собственное уравнение эллипса, напишите его в общем виде и начертите.
Все ли эллипсы имеют точку пересечения? Каково возможное количество точек пересечения эллипса? Объяснять.
Изучите и обсудите примеры эллипсов из реального мира.

Часть C: Дискуссионная доска
Ответы
Центр: (1,−2); ориентация: вертикальная; большой радиус: 7 единиц; малый радиус: 2 единицы; а=2; б=7
Центр: (0,−9); ориентация: горизонтальная; большой радиус: 3 единицы; малый радиус: 1 единица; а=3; б=1
Центр: (−5,−5); ориентация: горизонтальная; большой радиус: 3 единицы; малый радиус: 2 единицы; а=3; б=2
(х-3)225+(у-4)24=1
(х-5)26+(у+1)212=1
х2+(у+3)25=1
х -точки: (9±253,0); г -перехваты: нет
х -пересечения: (2,0); г — пересечения: (0,−6)
x — пересечения: нет; у — отрезки: (0,4±10)
х — деления: (±2,0); y — точки пересечения: (0,±5)
x225+y236=1
(х+4)216+(у+2)24=1
(х+1)29+(у-2)24=1;
(х+3)249+(у+1)24=1;
(х-6)264+(у+1)2=1;
х24+(у-5)236=1;
(х-2)281+(у-2)29=1;
(х+4)25+(у-2)24=1;
(х-1)25+(у+1)28=1;
(х-12)24+(у-1)29=1;
х24+(у-52)2=1;
x — пересечения: нет; г — пересечения: (0,−3)
х — отрезки: (3±33,0); г — пересечения: (0,−2)
х -точки: (10±105,0); г -перехваты: нет
5π5 квадратных блоков
π21 кв.

 |Singularity Hub
|Singularity Hub  |Наутилус выглядеть так, как если бы компас проследил его.
|Наутилус выглядеть так, как если бы компас проследил его.

 Если a>b, то эллипс в ширину больше, чем в высоту и считается горизонтальным эллипсом. Если a
Если a>b, то эллипс в ширину больше, чем в высоту и считается горизонтальным эллипсом. Если a