Упражнение эллипс: Nothing found for Elliptichesky Trenazher %23I 2

Как правильно заниматься на эллиптическом тренажере? (часть 1)

Упражнения на эллипсе: основные правила для новичков

Начинающие спортсмены смогут достичь идеальной формы, занимаясь на эллипсе, только зная, как с ним обращаться. Без данной информации смысл в тренажере теряется, как и эффективность упражнений. Данная статья поможет вам узнать больше о правилах упражнений при помощи эллипса.

Отрабатываем технику!

Исходное положение

Удивительно, но нередко спортсмен осуществляет ошибки в процессе упражнений с эллипсоидом еще до начала основной части тренировки. Избежать данных ошибок можно при помощи нескольких правил:

1. Большинство современных тренажеров поддаются регулировке шаговой длины. Если ваш тренажер оснащен такой функцией, настройте режим, при котором вы сможете длительное время шагать достаточно широко.
2. Схватитесь за поручни и станьте на педалях. Самое главное в этом деле – удобство.
3. Не забудьте выпрямить спину! Сутулая спина принесет вам больше вреда, нежели пользы.
4. Обхватите рычаги тренажера достаточно плотно (костяшки рук не должны белеть).
5. Стопы ног должны плотно прилегать к педалям.

Заняли правильное положение? Поздравляем! Приступайте к следующим этапам тренировки.

Движения

1. Перед стартом начинающему спортсмену нужно четко определиться, какая нога у него ведущая. К примеру, если ведет правая нога, она же совершает толчки вперед. В это время левая рука тянет к себе поручень.
2. Не допускайте пауз. Выполняйте аналогичные движения разноименными конечностями. Приступайте к упражнениям медленно, а через некоторое время ускоряйтесь (конечно, если это позволяет состояние здоровья).
3. Не останавливайтесь резко. Плавно замедляйте движения, переходя от бега к медленному шагу, а от шага – к полной остановке.
4. Сходите с эллипсоида только после полного прекращения упражнений.

Тренировки на эллипсе: чего делать нельзя?

Тренировка на эллипсоиде даст положительный результат, если вы учтете несколько маленьких секретов. Возможно, учесть все секреты удастся не сразу, однако в любом случае следует сохранить их в голове.

• Не переносите вес с одной ноги, которая выступает в качестве опоры, на другую. Не следует допускать перегрузки: распределять вес нужно правильно. Помните: центр тяжести находится в центре тела!
• Нередко спортсмены надевают термобелье для быстрого похудения. Делать этого ни в коем случае нельзя! В таком случае сердце будет терпеть огромную нагрузку.
• Новички нередко падают с тренажеров. Не бойтесь! Это частая проблема новичков. Для того чтобы ее избежать, займите максимально устойчивое положение.
• Не расслабляйтесь слишком сильно, однако перенапрягаться тоже нельзя. Во время воздействия одной ноги на педаль вторая должна оставаться в тонусе.
• Нередко спортсмены занимаются на эллипсоиде, перенося всю нагрузку с ног в руки. Спортивный агрегат должен развивать мышцы пояса и ног, поэтому не следует полагаться только на руки, буквально «лежа» на поручнях.
• Дышите равномерно. Ни в коем случае не задерживайте дыхание для быстрой прокрутки педалей на максимуме, после которого с тренажера сходят. Это принесет больше вреда организму, чем пользы.

Советы от AppleGate-Fitness

1. Смотрите под ноги перед тем, как ступить на тренажер. Не стоит накладываться всем весом на тренажер, педаль которого расположена не внизу.
2. Не старайтесь подражать опытным спортсменам. Даже если вы видите человека, уверенно и быстро пользующегося эллипсоидом, не держась за руки, не следует нарушать собственный темп тренировки. Слишком интенсивные занятия могут привести к головокружению, нарушению сердечного ритма и потере равновесия.
3. Ваши кроссовки должны обеспечивать отличное сцепление с поверхностью.
4. В случае если вам захотелось сделать паузу, начните замедляться, остановитесь и сойдите с тренажера.
5. Ускоряйтесь плавно. Не следует выкладываться на максимум в первые три – пять минут упражнений: в таком случае вы быстрее устанете, собьете сердечный ритм и получите головокружение. К тому же, резкое начало тренировки приведет вас к вывихам, растяжениям и ушибам.

Продолжение читайте далее:

Как правильно заниматься на эллиптическом тренажере? (часть 2)

«Сколько нужно заниматься на эллипсе чтобы похудеть?»

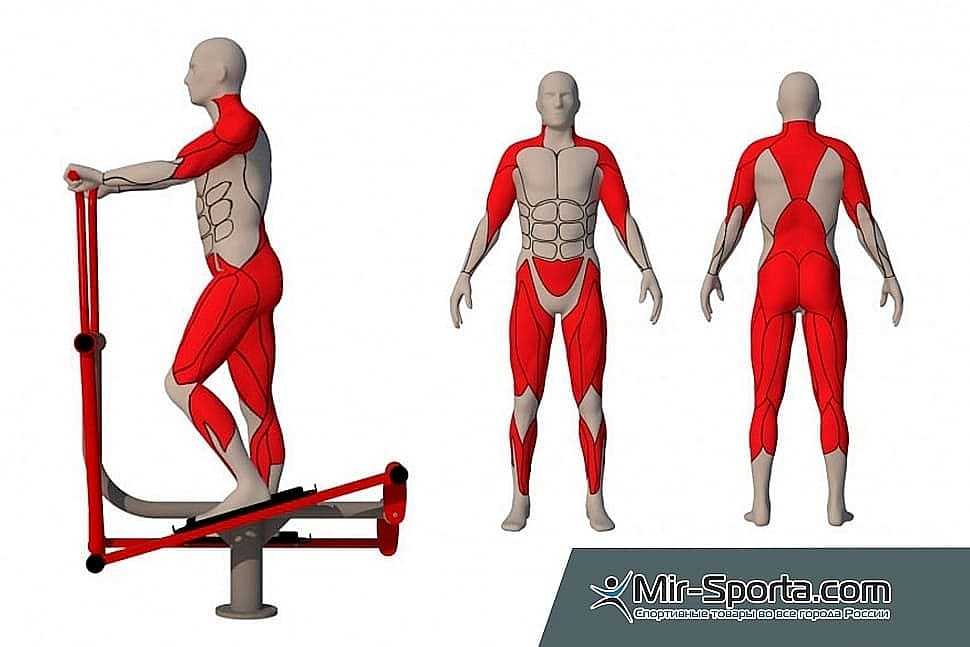
Эллипсоид — универсальный тренажер, который равномерно прокачивает все группы мышц. Это обязательный инструмент всех фитнес залов. Комбинированный тренажер подходит не только для физической активности, но и эффективен при похудении. Но для того чтобы тренировки были по-настоящему результативными необходимо выполнять основные правила.

КАК ПРАВИЛЬНО ЗАНИМАТЬСЯ

Стоит отметить, что любая тренировка будет полезна для организма, даже если ее технология будет нарушена. Активные упражнения предполагают энергетические затраты, чем больше потрачено калорий — тем выше результат. Но чтобы достичь этого результата нередко приходится попотеть.

Помимо активных тренировок придется пересмотреть режим и рацион питания. Только комплексный подход поможет решить задачу похудения. При этом важно чтобы была достигнута отрицательная разница между поступившей с едой энергией и затраченной во время бодрствования. Упражнения выполняются через 1,5-2 часа после последнего приема пищи. Во время занятий корпус должен быть ровным, голова прямой, живот втянут, а шаг делается на всю стопу. Далее рассмотрим вариант длительной тренировки.

Длительная тренировка на эллиптическом тренажере отлично подходит для желающих сбросить вес. Преимущества:

• Быстрое сжигание жировых отложений;
• Поднятие мышечного тонуса;
• Восстановление дыхательной, а также нормальной работы сердечно-сосудистой системы.

Длительная тренировка предполагает занятия в течение 1 часа. Нагрузка должна быть равномерной для того чтобы не делать перерывов даже на кратковременный отдых. Интенсивность выбирается самостоятельно. За 1 тренировку необходимо потратить 600 ккал.

Программа для похудения включает 5 занятий.

На первом проводится легкая разминка, которая длится буквально 5 минут. Затем выполняется непосредственная тренировка с контролем пульса. Он должен превышать 50-60% от максимального значения. Норма пульса рассчитывается по специальной формуле с указанием возраста.

Второе занятие также начинается с разминки. Потом в течение 5 минут повышенная интенсивность, через 3 минуты — максимальная. Чередуем эти 2 пункта и завершающий этап — замедление.

Третье занятие стартует с тренировки средней интенсивности с постепенным наращиванием темпов в течение 15 минут. Затем интенсивность уменьшается.

Четвертое занятие — упражнения выполняются 30 минут. Все это время соблюдается средний темп и малое сопротивление.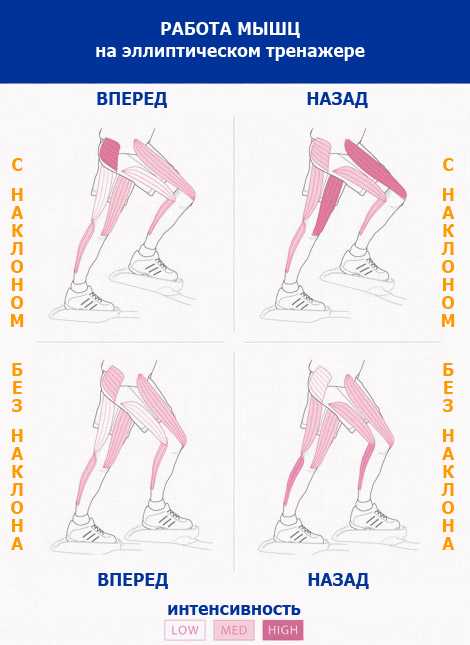

В начале пятого занятия проводится легкая разминка, затем в течение 3 минут нагрузка должна резко возрасти, 2 минуты выделяется на абсолютный максимум. Эту технологию необходимо повторить 4 раза и в конце сделать заминку.

Далее поговорим об интервальной тренировке.

Интервальная тренировка на эллипсоиде является более результативной, чем длительная, но здесь существуют ограничения по количеству — не рекомендуется заниматься на тренажере больше 2 раз в неделю. Интервальная программа выглядит следующим образом:

• Первая пятиминутка начинается с замедленного темпа. Количество шагов примерно 120шт в минуту;
• После этого делаем минутные интервалы, это от 120 до 130 шагов. На последней минуте делаем 115 шагов и так нужно повторить 6 раз подряд;
• Завершающим этапом делаем 2 минуты по 140 шагов и далее шагаем последние 5 минут в размеренном темпе.

Сколько нужно заниматься

Точного ответа на поставленный вопрос нет. Все сугубо индивидуально. Если человек только недавно встал на тренажер, то нагрузка должна быть не более получаса 3 раза в неделю. В ходе занятий нужно выполнять 50 шагов в минуту, а пульс должен находиться в пределах 70% от максимальных показателей. Средний срок адаптации организма к нагрузкам составляет 7 недель. Далее нужно постепенно наращивать интенсивность. Адаптированные люди и спортсмены занимаются на эллипсоидах практически ежедневно. Именно поэтому если нужно сбросить вес или подтянуть форму при помощи эллиптического тренажера, то нужно уделять упражнениям достаточное количество времени.

Сколько калорий сжигается на эллиптических тренажерах

Все индивидуально. Здесь играет роль особенность самого организма, количество шагов в ходе тренировок и оптимальная нагрузка. У мужчин одни показатели, у женщин — другие.

На сколько можно похудеть

Если строго соблюдать все вышеперечисленные правила, то первый результат будет заметен уже после 1 месяца активных занятий на эллипсоиде.

Точное число сброшенных килограмм назвать нельзя, поскольку это зависит от множества факторов. Но если занятия будут длиться в среднем по полчаса и пульс будет находиться в районе 130 ударов в минуту, то результат будет впечатляющий.

Заключение

Эллиптический тренажер — отличное решение для похудения и поднятия физической активности. Он почти не имеет противопоказаний, а это значит, что тренироваться могут люди разных возрастов и массы тела. Тип тренировок выбирается самостоятельно, главное чтобы они были регулярными, и тогда результат не заставит себя ждать. Выполняйте все правила, контролируйте процесс, регулярность подходов и вы получите фигуру своей мечты!

В данной статье я дал всего несколько советов на тему: «Сколько нужно заниматься на эллипсе чтобы похудеть?». Надеюсь, что эта информация поможет вам найти ответы на вопросы в пути к поставленным целям.

9.1.1E: Эллипсы (упражнения) — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

20758

раздел 9. 1, упражнения

В задачах 1–4 сопоставьте каждый график с одним из уравнений A–D. 92 = 12\)

В задачах 15–16 напишите уравнение для графика.

15. 16.

В задачах 17–20 найти стандартную форму уравнения эллипса, удовлетворяющую заданным условиям.

17. Центр (0,0), длина большой горизонтальной оси 64, длина малой оси 14

18. Центр (0,0), длина большой вертикальной оси 36, длина малой оси 18

19. Центр (0,0, 0), вершина (0,3), \(b = 2\)

20. Центр (0,0), вершина (4,0), \(b = 3\)

В задачах 21–28, сопоставьте каждый график с уравнениями A-H. 92 + 36y = — 4\)

В задачах 39–40 напишите уравнение для графика.

39. 40.

В задачах 41–42 найти стандартную форму уравнения эллипса, удовлетворяющую заданным условиям.

41. Центр (-4, 3), вершина (-4, 8), точка на графике (0, 3)

42. Центр (1, -2), вершина (-5, -2), точка на графике (1, 0)

43. Окно Окно в форме полуэллипса имеет ширину 12 футов и высоту 4 фута. Какова высота окна над основанием в 5 футах от центра?

44. Окно Окно в форме полуэллипса имеет ширину 16 футов и высоту 7 футов. Какова высота окна над основанием в 4 футах от центра?

45. Мост Мост через реку поддерживается полуэллиптической аркой. Ширина реки 150 футов. В центре арка возвышается на 60 футов над рекой. Проезжая часть находится на 5 футов выше центра арки. Каково вертикальное расстояние между проезжей частью и аркой в ​​45 футах от центра?

46. Мост Мост через реку поддерживается полуэллиптической аркой. Ширина реки 1250 футов. В центре арка возвышается на 175 футов над рекой. Проезжая часть находится на 3 фута выше центра арки. Каково вертикальное расстояние между проезжей частью и аркой в ​​600 футах от центра?

47. Беговая дорожка Эллиптическая беговая дорожка имеет длину 100 футов и ширину 90 футов. Какова ширина беговой дорожки в 20 футах от вершины на большой оси? 92 = 1\)

В задачах 53-72 найти стандартную форму уравнения эллипса, удовлетворяющую заданным условиям.

53. Вершины большой оси (\(\pm\)3,0), \(c= 2\)

54. Вершины большой оси (0, \(\pm\)7), \(c= 4 \)

55. Фокусы (0, \(\pm\)5) и длина большой оси 12

56. Фокусы (\(\pm\)3, 0) и длина большой оси 8

57. Фокусы ( \(\pm\)5, 0), вершины (\(\pm\)7, 0)

58. Фокусы (0,\(\pm\)2), вершины (0,\(\pm\) 3)

59. Фокусы (0, \(\pm\)4) и \(x\)-перехваты (\(\pm\)2, 0)

60. Фокусы (\(\pm\)3, 0) и \( y\)-отрезки (0, \(\pm\)1)

61. Центр (0, 0), длина большой оси 8, фокусы на \(x\)-оси, проходит через точку \(\left( 2,\sqrt 6 \right)\)

62. Центр (0, 0), длина большой оси 12, фокусы на \(y\)-оси, проходит через точку \(\left( \sqrt {10} , 4 \справа)\)

63. Центр (-2, 1), вершина (-2, 5), фокус (-2, 3)

64. Центр (-1, -3), вершина (-7 , -3), фокус (-4, -3)

65. Фокусы (8, 2) и (-2, 2), длина большой оси 12

66. Фокусы (-1, 5) и (-1, -3), длина большой оси 14

67. Вершины (3, 4) и (3, -6), \(с= 2\)

68. Вершины (2, 2) и (-4, 2), \(с= 2\)

69. Центр (1, 3), фокус (0, 3), проходит через точку (1, 5)

70. Центр (-1, -2), фокус (1, -2), проходит через точку (2, — 2)

71. Фокус (-15, -1), вершины (-19, -1) и (15, -1)

72. Фокус (-3, 2), вершины (-3, 4) и (-3, -8)

73. Шепчущая галерея Если эллиптическая шепчущая галерея имеет длину 80 футов и ширину 25 футов, то на каком расстоянии от центра комнаты нужно стоять на главной оси эллипса, чтобы испытать эффект шепота? Округлить до двух знаков после запятой.

74. Бильярд Некоторые бильярдные столы имеют эллиптическую форму и имеют отмеченные на столе фокусы. Если такой 8 футов в длину и 6 футов в ширину, как далеко фокусы от центра эллипса? Округлить до двух знаков после запятой.

75. Планетарные орбиты Орбиты планет вокруг Солнца имеют приблизительно эллиптическую форму с Солнцем в фокусе. Афелий — это наибольшее расстояние планеты от Солнца, а перигелий — самое короткое. 2}{k} = 1\) софокусны. 92} = 1\), где \(а > Ь\).

Ответить

1. Д

3. Б

5. Вершины \((0, \pm 5)\), концы малой оси \((\pm 2, 0)\), большая длина = 10, малая длина = 4

7. Вершины \((\pm 5, 0)\), концы малой оси \((0, \pm 1)\), большая длина = 4, малая длина = 2

9. Вершины \((\pm 5, 0)\), концы малой оси \((0, \pm 1)\), большая длина = 10, малая длина = 2 92}{9} = 1\)

21. Б

23. С

25. Ф

27. Г

29. Центр (1, -2), вершины (6, -2) и (-4, -2), концы малой оси (1, 0) и (1, -4), большая длина = 10, малая длина = 4

31. Центр (-2, 3), вершины (-2, 8) и (-2, -2), концы малой оси (-1, 3) и (-3, 3), большая длина = 10, второстепенная длина = 2

33. Центр (-1, 0), вершины (-1, 4) и (-1, -4), концы малой оси (-1, 0) и (3, 0), большая длина = 8, малая длина = 4 92}{а}\).

---

9.1.1E: Ellipses (упражнения) распространяется по незаявленной лицензии и был создан, изменен и/или курирован LibreTexts.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Версия лицензии

   2,0

2. Теги

   На этой странице нет тегов.

11.3 Эллипсы — Алгебра среднего уровня 2e

Цели обучения

К концу этого раздела вы сможете:

• График эллипса с центром в начале координат
• Найти уравнение эллипса с центром в начале координат
• Нарисуйте эллипс с центром не в начале координат
• Решить приложение с эллипсами

Приготовься 11,7

Прежде чем приступить к работе, пройдите этот тест на готовность.

График y=(x−1)2−2y=(x−1)2−2 с использованием преобразований.
Если вы пропустили эту проблему, просмотрите пример 9.57.

Приготовься 11,8

Заполните квадрат: x2−8x=8.x2−8x=8.
Если вы пропустили эту проблему, просмотрите пример 9.12.

Приготовься 11,9

Пишите в стандартной форме. y=2×2−12x+14y=2×2−12x+14
Если вы пропустили эту задачу, просмотрите пример 9.59.

Нарисуйте эллипс с центром в начале координат

Следующим коническим сечением, которое мы рассмотрим, является эллипс. Мы определяем эллипс как все точки на плоскости, где сумма расстояний от двух фиксированных точек постоянна. Каждая из заданных точек называется фокусом эллипса.

Эллипс

Эллипс — это все точки на плоскости, где сумма расстояний от двух фиксированных точек постоянна. Каждая из неподвижных точек называется фокус эллипса.

Мы можем нарисовать эллипс, взяв гибкую нить фиксированной длины и прикрепив ее концы к двум кнопкам. Мы используем ручку, чтобы натянуть нить и повернуть ее вокруг двух кнопок. Получившаяся фигура представляет собой эллипс.

Прямая, проведенная через фокусы, пересекает эллипс в двух точках. Каждая точка называется вершиной эллипса. Отрезок, соединяющий вершины, называется большой осью . Середина сегмента называется 9.0122 центр эллипса. Отрезок, перпендикулярный большой оси, проходящий через центр и пересекающий эллипс в двух точках, называется малой осью .

Ранее мы упоминали, что наша цель — связать геометрию коники с алгеброй. Размещение эллипса в прямоугольной системе координат дает нам такую ​​возможность. На рисунке мы разместили эллипс так, чтобы фокусы ((−c,0),(c,0))((−c,0),(c,0)) находились на оси x , а центр является источником.

В определении указано, что сумма расстояний от фокусов до точки (x,y)(x,y) постоянна. Таким образом, d1+d2d1+d2 — это константа, которую мы будем называть 2a2a, поэтому d1+d2=2a.d1+d2=2a. Мы будем использовать формулу расстояния, чтобы привести нас к алгебраической формуле для эллипса.

Используйте формулу расстояния, чтобы найтиd1,d2.d1+d2=2a(x−(−c))2+(y−0)2+(x−c)2+(y−0)2=2aПосле исключения упрощая, получаем:x2a2+y2a2−c2=1Чтобы упростить уравнение эллипса, weleta2−c2=b2. Итак, уравнение эллипса с центром в начале координат в стандартной форме имеет вид:x2a2+y2b2=1Используем формулу расстояния, чтобы найтиd1 ,d2.d1+d2=2a(x−(−c))2+(y−0)2+(x−c)2+(y−0)2=2aПосле удаления радикалов и упрощения получаем:x2a2+ y2a2−c2=1Чтобы упростить уравнение эллипса, weleta2−c2=b2. Таким образом, уравнение эллипса с центром в начале координат в стандартной форме имеет вид:x2a2+y2b2=1

Чтобы нарисовать эллипс, полезно знать точки пересечения. Мы найдем x -перехватов и y -перехватов, используя формулу.

y-перехватыLetx=0. x2a2+y2b2=102a2+y2b2=1y2b2=1y2=b2y=±bx-перехватыLety=0.x2a2+y2b2=1x2a2+02b2=1x2a2=1×2=a2x=±aОни-перехваты равны (0, b)и(0,−b).X-перехваты равны(a,0)и(−a,0).y-перехватыLetx=0.x2a2+y2b2=102a2+y2b2=1y2b2=1y2=b2y=±bx- interceptsLety=0.x2a2+y2b2=1x2a2+02b2=1x2a2=1×2=a2x=±aОни-перехваты равны (0,b)и(0,−b).X-перехваты равны(a,0)и(−a, 0).

Стандартная форма уравнения эллипса с центром (0,​0)(0,​0)

Стандартная форма уравнения эллипса с центром (0,​​0),(0,​0 ), равно

x2a2+y2b2=1x2a2+y2b2=1

x -отрезков равны (a,0)(a,0) и (−a,0).(−a,0).

y -отрезки равны (0,b)(0,b) и (0,−b).(0,−b).

Обратите внимание, что когда большая ось расположена горизонтально, значение a будет больше, чем значение b и когда большая ось вертикальна, значение b будет больше, чем значение a . Мы будем использовать эту информацию для построения эллипса с центром в начале координат.

Эллипс с центром (0,0)(0,0)
x2a2+y2b2=1x2a2+y2b2=1	а>ба>б	б>аб>а
Большая ось	на оси x -.	на и -ось.
x -пересечения	(-а, 0), (- а, 0), (а, 0) (а, 0)
у -перехваты	(0,−b),(0,−b),(0,b)(0,b)

Стол 11. 2

Пример 11.20

Как построить эллипс с центром (0, 0)

График: x24+y29=1.x24+y29=1.

Решение

Попробуй это 11.39

График: x24+y216=1.x24+y216=1.

Попробуй это 11.40

График: x29+y216=1.x29+y216=1.

Мы суммируем шаги для справки.

Как

Как построить эллипс с центром (0,0).(0,0).

1. Шаг 1. Запишите уравнение в стандартной форме.
2. Шаг 2. Определите, является ли главная ось горизонтальной или вертикальной.
3. Шаг 3. Найдите конечные точки большой оси.
4. Шаг 4. Найдите конечные точки малой оси
5. Шаг 5. Нарисуйте эллипс.

Иногда наше уравнение сначала нужно привести к стандартной форме.

Пример 11.21

График x2+4y2=16.x2+4y2=16.

Решение

Мы признаем это уравнением эллипса , поскольку члены x и y равны в квадрате и имеют разные коэффициенты.	х2+4у2=16х2+4у2=16
Чтобы получить уравнение в стандартной форме, разделите с обеих сторон на 16, так что уравнение равно на 1.	х216+4у216=1616х216+4у216=1616
Упрощение.	х216+у24=1х216+у24=1
Уравнение имеет стандартную форму. Центр эллипса находится в начале координат.	Центр равен (0,0).(0,0).
Так как 16>416>4 и 16 в члене x2x2, большая ось горизонтальна.
a2=16,a=±4a2=16,a=±4   b2=4,b=±2b2=4,b=±2	Вершины: (4,0),(−4,0). (4,0),(−4,0). Конечные точки малой оси: (0,2),(0,−2).(0,2),(0,−2).
Нарисуйте параболу.

Попробуй это 11.41

График 9×2+16y2=144,9×2+16y2=144.

Попробуй это 11.42

График 16×2+25y2=400,16×2+25y2=400.

Найдите уравнение эллипса с центром в начале координат

Если нам дан график эллипса, мы можем найти уравнение эллипса.

Пример 11.22

Найдите уравнение показанного эллипса.

Решение

Мы распознаем это как эллипс с центром в начале координат.	x2a2+y2b2=1x2a2+y2b2=1
Поскольку большая ось горизонтальна, а расстояние от центра до вершины равно 4, мы знаем, что a=4a=4 и, следовательно, a2=16a2=16.	х216+y2b2=1×216+y2b2=1
Малая ось вертикальна, а расстояние от центра до эллипса равно 3, мы знаем, что b=3b=3, поэтому b2=9б2=9.	х216+у29=1х216+у29=1

Попробуй это 11.43

Найдите уравнение показанного эллипса.

Попробуй это 11.44

Найдите уравнение показанного эллипса.

Нарисуйте эллипс с центром не в начале координат

Все эллипсы, которые мы рассматривали до сих пор, были центрированы в начале координат. Теперь мы рассмотрим эллипсы с центром в (h,k).(h,k).

Уравнение (x−h)2a2+(y−k)2b2=1(x−h)2a2+(y−k)2b2=1 и когда a>b,a>b, большая ось горизонтальна, поэтому расстояние от центра до вершины и . Когда b>a,b>a, большая ось вертикальна, поэтому расстояние от центра до вершины равно b .

Стандартная форма уравнения эллипса с центром (h,k)(h,k)

Стандартная форма уравнения эллипса с центром (h,k),(h,k):

(x− h)2a2+(y−k)2b2=1(x−h)2a2+(y−k)2b2=1

Когда a>b,a>b, большая ось горизонтальна, поэтому расстояние от центра до вершины это .

Когда b>a,b>a, большая ось вертикальна, поэтому расстояние от центра до вершины равно б .

Пример 11.23

График: (x−3)29+(y−1)24=1.(x−3)29+(y−1)24=1.

Решение

Уравнение имеет стандартный вид: (x−h)2a2+(y−k)2b2=1.(x−h)2a2+(y−k)2b2=1.	(х-3)29+(у-1)24=1(х-3)29+(у-1)24=1
Центр эллипса находится в точке (h,k).(h,k).	Центр равен (3,1).(3,1).
Так как 9>49>4 и 9 в члене x2x2, большая ось горизонтальна.
a2=9,a=±3a2=9,a=±3   b2=4,b=±2b2=4,b=±2	Расстояние от центра до вершин равно 3. Расстояние от центра до конечных точек малой оси равно 2.
Нарисуйте эллипс.

Попробуй это 11.45

График: (x+3)24+(y−5)216=1.(x+3)24+(y−5)216=1.

Попробуй это 11.46

График: (x−1)225+(y+3)216=1.(x−1)225+(y+3)216=1.

Если мы посмотрим на уравнения x29+y24=1×29+y24=1 и (x−3)29+(y−1)24=1, (x−3)29+(y−1)24=1, мы видим, что они оба эллипсы с a=3a=3 и b=2.b=2. Так они будут иметь одинаковый размер и форму. Они отличаются тем, что у них нет одного и того же центра.

Обратите внимание на график выше, что мы могли бы изобразить (x−3)29+(y−1)24=1(x−3)29+(y−1)24=1 с помощью переводов. Мы переместили исходный эллипс вправо на 3 единицы, а затем вверх на 1 единицу.

В следующем примере мы будем использовать метод перевода для построения эллипса.

Пример 11.

24

График (x+4)216+(y−6)29=1(x+4)216+(y−6)29=1 по переводу.

Решение

Этот эллипс будет иметь тот же размер и форму, что и x216+y29=1×216+y29=1, центр которого равен (0,0).(0,0). Сначала нарисуем этот эллипс.

Центр равен (0,0).(0,0).	Центр (0,0)(0,0)
Поскольку 16>9,16>9, большая ось горизонтальна.
a2=16,a=±4a2=16,a=±4   b2=9,b=±3b2=9,b=±3	Вершины: (4,0),(−4,0).(4,0),(−4,0). Конечные точки малой оси: (0,3),(0,−3).(0,3),(0,−3).
Нарисуйте эллипс.
Исходное уравнение имеет стандартную форму: (x−h)2a2+(y−k)2b2=1.(x−h)2a2+(y−k)2b2=1.	(х-(-4))216+(у-6)29=1(х-(-4))216+(у-6)29=1
Центр эллипса находится в точке (h,k).(h,k).	Центр равен (−4,6).(−4,6).
Перенесем график x216+y29=1×216+y29=1 на четыре единиц влево, а затем вверх на 6 единиц. Убедитесь, что центр равен (−4,6).(−4,6). Новый эллипс — это эллипс, уравнение которого равно (x+4)216+(y−6)29=1.(x+4)216+(y−6)29=1.

Попробуй это 11.47

График (x−5)29+(y+4)24=1(x−5)29+(y+4)24=1 по переводу.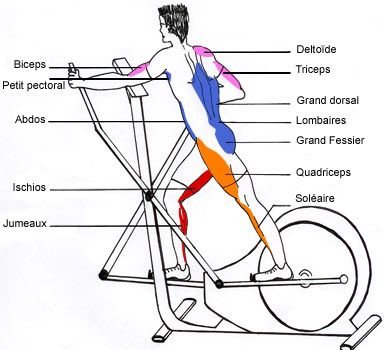

Попробуй это 11.48

График (x+6)216+(y+2)225=1(x+6)216+(y+2)225=1 по переводу.

Если в уравнении есть x2x2 и y2y2 с разными коэффициентами, мы проверяем, является ли оно многоточием, придавая ему стандартную форму. После этого мы сможем построить график уравнения.

Пример 11.25

Запишите уравнение x2+4y2−4x+24y+24=0x2+4y2−4x+24y+24=0 в стандартной форме и на графике.

Решение

Приведем уравнение к стандартной форме, заполнив квадраты в обоих х и и .

	x2+4y2−4x+24y+24=0x2+4y2−4x+24y+24=0
Переписать, сгруппировав термины размером x и термины y .
Сделать коэффициенты x2x2 и y2y2 равными 1.
Заполните квадраты.
Запишите в виде биномиальных квадратов.
Разделите обе стороны на 16, чтобы получить 1 справа.
Упрощение.
Уравнение в стандартной форме, (x−h)2a2+(y−k)2b2=1(x−h)2a2+(y−k)2b2=1
Центр эллипса находится в точке (h,k). (h,k).	Центр равен (2,−3).(2,−3).
Так как 16>416>4 и 16 в члене x2x2, большая ось горизонтальна.   a2=16,a=±4a2=16,a=±4   b2=4,b=±2b2=4,b=±2	Расстояние от центра до вершин равно 4. Расстояние от центра до конечных точек малой оси равно 2.
Нарисуйте эллипс.

Попробуй это 11.49

ⓐ Запишите уравнение 6×2+4y2+12x−32y+34=06×2+4y2+12x−32y+34=0 в стандартной форме и график ⓑ.

Попробуй это 11.50

ⓐ Запишите уравнение 4×2+y2−16x−6y+9=04×2+y2−16x−6y+9=0 в стандартной форме и график ⓑ.

Решение приложения с помощью эллипсов

Орбиты планет вокруг Солнца следуют эллиптическим траекториям.

Пример 11.26

Плутон (карликовая планета) движется по эллиптической орбите вокруг Солнца. Ближайший Плутон подходит к Солнцу примерно на 30 астрономических единиц (а.е.), а самый дальний — примерно на 50 а.е. Солнце является одним из фокусов эллиптической орбиты. Позволив эллипсу центрироваться в начале координат и обозначив оси в а.е., орбита будет выглядеть, как показано на рисунке ниже. Используйте график, чтобы написать уравнение для эллиптической орбиты Плутона.

Решение

Мы распознаем это как эллипс с центром в начале координат.	x2a2+y2b2=1x2a2+y2b2=1
Поскольку большая ось горизонтальна, а расстояние от центра до вершины равно 40, мы знаем, что a=40a=40 и, следовательно, a2=1600a2=1600.	x21600+y2b2=1×21600+y2b2=1
Малая ось вертикальна, но конечные точки не указаны. Чтобы найти bb, мы будем использовать положение Солнца. Поскольку Солнце находится в фокусе эллипса в точке (10,0)(10,0), мы знаем, что c=10c=10. Используйте это, чтобы решить для b2b2.	b2=a2−c2b2=402−102b2=1600−100b2=1500b2=a2−c2b2=402−102b2=1600−100b2=1500
Подставьте a2a2 и b2b2 в стандартную форму эллипса.	x21600+y21500=1×21600+y21500=1

Попробуй это 11.51

Планета движется по эллиптической орбите вокруг своего солнца. Ближайшая планета подходит к Солнцу примерно на 20 а.е., а самая дальняя — примерно на 30 а.е. Солнце является одним из фокусов эллиптической орбиты. Позволив эллипсу центрироваться в начале координат и обозначив оси в а.е., орбита будет выглядеть, как показано на рисунке ниже. Используйте график, чтобы написать уравнение для эллиптической орбиты планеты.

Попробуй это 11.52

Планета движется по эллиптической орбите вокруг своего солнца. Ближе всего планета подходит к Солнцу примерно на 20 а. е., а дальше всего примерно на 50 а.е. Солнце является одним из фокусов эллиптической орбиты. Позволив эллипсу центрироваться в начале координат и обозначив оси в а.е., орбита будет выглядеть, как показано на рисунке ниже. Используйте график, чтобы написать уравнение для эллиптической орбиты планеты.

Раздел 11.3 Упражнения

Практика делает совершенным

График эллипса с центром в начале координат

В следующих упражнениях постройте график каждого эллипса.

99.

х24+у225=1х24+у225=1

100.

х29+у225=1х29+у225=1

101.

х225+у236=1х225+у236=1

102.

х216+у236=1х216+у236=1

103.

х236+у216=1х236+у216=1

104.

х225+у29=1х225+у29=1

105.

х2+у24=1х2+у24=1

106.

х29+у2=1х29+у2=1

107.

4×2+25y2=1004×2+25y2=100

108.

16×2+9y2=14416×2+9y2=144

109.

16×2+36y2=57616×2+36y2=576

110.

9×2+25y2=2259×2+25y2=225

Найдите уравнение эллипса с центром в начале координат

В следующих упражнениях найдите уравнение эллипса, изображенного на графике.

111.

112.

113.

114.

График эллипса с центром не в начале координат

В следующих упражнениях постройте график каждого эллипса.

115.

(х+1)24+(у+6)225=1(х+1)24+(у+6)225=1

116.

(х-3)225+(у+2)29=1(х-3)225+(у+2)29=1

117.

(х+4)24+(у-2)29=1(х+4)24+(у-2)29=1

118.

(х-4)29+(у-1)216=1(х-4)29+(у−1)216=1

В следующих упражнениях постройте график каждого уравнения в виде переноса.

119.

(х-3)24+(у-7)225=1(х-3)24+(у-7)225=1

120.

(х+6)216+(у+5)24=1(х+6)216+(у+5)24=1

121.

(х-5)29+(у+4)225=1(х-5)29+(у+4)225=1

122.

(х+5)236+(у-3)216=1(х+5)236+(у-3)216=1

В следующих упражнениях ⓐ напишите уравнение в стандартной форме и ⓑ нарисуйте.

123.

25×2+9y2-100x-54y-44=025×2+9y2-100x-54y-44=0

124.

4×2+25y2+8x+100y+4=04×2+25y2+8x+100y+4=0

125.

4×2+25y2-24x-64=04×2+25y2-24x-64=0

126.

9×2+4y2+56y+160=09×2+4y2+56y+160=0

В следующих упражнениях нарисуйте уравнение.

127.

х=-2(у-1)2+2х=-2(у-1)2+2

128.

х2+у2=49х2+у2=49

129.

(х+5)2+(у+2)2=4(х+5)2+(у+2)2=4

130.

у=-х2+8х-15у=-х2+8х-15

131.

(х+3)216+(у+1)24=1(х+3)216+(у+1)24=1

132.

(х-2)2+(у-3)2=9(х-2)2+(у-3)2=9

133.

х225+у236=1х225+у236=1

134.

х=4(у+1)2-4х=4(у+1)2-4

135.

х2+у2=64х2+у2=64

136.

х29+у225=1х29+у225=1

137.

у=6х2+2х-1у=6х2+2х-1

138.

(х-2)29+(у+3)225=1(х-2)29+(у+3)225=1

Решение приложения с эллипсами

139.

Планета движется по эллиптической орбите вокруг своего солнца. Ближе всего планета подходит к Солнцу примерно на 10 а.е., а дальше всего примерно на 30 а.е. Солнце является одним из фокусов эллиптической орбиты. Позволив эллипсу центрироваться в начале координат и обозначив оси в а.е., орбита будет выглядеть, как показано на рисунке ниже. Используйте график, чтобы написать уравнение для эллиптической орбиты планеты.

140.

Планета движется по эллиптической орбите вокруг своего солнца. Ближе всего планета подходит к Солнцу примерно на 10 а.е., а дальше всего примерно на 70 а. е. Солнце является одним из фокусов эллиптической орбиты. Позволив эллипсу центрироваться в начале координат и обозначив оси в а.е., орбита будет выглядеть, как показано на рисунке ниже. Используйте график, чтобы написать уравнение для эллиптической орбиты планеты.

141.

Комета движется по эллиптической орбите вокруг Солнца. Ближе всего комета подходит к Солнцу примерно на 15 а.е., а дальше всего на 85 а.е. Солнце является одним из фокусов эллиптической орбиты. Позволив эллипсу центрироваться в начале координат и обозначив оси в а.е., орбита будет выглядеть, как показано на рисунке ниже. Используйте график, чтобы написать уравнение для эллиптической орбиты кометы.

142.

Комета движется по эллиптической орбите вокруг Солнца. Ближе всего комета подходит к Солнцу примерно на 15 а.е., а дальше всего примерно на 95 а.е. Солнце является одним из фокусов эллиптической орбиты. Позволив эллипсу центрироваться в начале координат и обозначив оси в а. е., орбита будет выглядеть, как показано на рисунке ниже. Используйте график, чтобы написать уравнение для эллиптической орбиты кометы.

Письменные упражнения

143.

Своими словами дайте определение эллипсу и напишите уравнение эллипса с центром в начале координат в стандартной форме. Нарисуйте эскиз эллипса, обозначив центр, вершины, большую и малую оси.

144.

Объясните своими словами, как получить оси из уравнения в стандартной форме.

145.

Сравните и сопоставьте графики уравнений x24+y29=1×24+y29=1 и x29+y24=1.×29+y24=1.

146.

Объясните своими словами разницу между вершиной и фокусом эллипса.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.