Метод RANC в Клинике на Мате Залки
- Главная
- О клинике
Метод RANC заключается в восстановлении нормальной активности нервных центров, оказав на них влияние через короткий, мощный поток болевых импульсов, посредством нанесения болевого раздражения определённых участков мышц.
Трапециевидные мышцы, из-за особенностей своей иннервации являются уникальным местом на теле человека. Они иннервируются добавочным нервом, который берёт начало от многочисленных ядер ствола головного мозга. В стволе и спинном мозге ядра добавочного нерва анатомически и функционально тесно связаны с ядрами ретикулярной формации, которая контролирует работу всех отделов головного мозга. Эта особенность делает их своеобразной картой мозга, на которой болезненные (напряжённые) участки соответствуют отделам и центрам мозга, которые функционируют в режиме повышенной активности.
Повышение активности одних мозговых центров неизбежно вызывает снижение активности других, которые имеют с ними тесные функциональные и анатомические связи. Устойчивое рассогласование в работе и взаимодействии мозговых центров регуляции ведет к появлению соответствующих сбоев в работе различных органов и систем нашего организма. Эти нарушения носят название симптомов. Несколько симптомов объединяясь, образуют синдром, или как ещё принято говорить болезнь.
Быстрое, но мощное болевое раздражение напряжённых участков трапециевидных мышц, при помощи инъекций какого либо болезненного препарата (например: витамина В 6, В 12, Магнезии, Эуфиллина, Анальгина) вызывает передачу потока импульсов через добавочный нерв в ствол головного мозга, а там импульсы передаются на ядра ретикулярной формации и проходят по её волокнам в мозговые центры, работающие в режиме перевозбуждения. Получив этот импульс энергии мозговые центры, в том числе и сама ретикулярная формация, начинают тут же менять свою активность.
Методу RANC лучше всего поддаются заболевания, которые традиционно считаются функциональными расстройствами, то есть когда разрушения в организме минимальны. Но, всё относительно, поскольку функциональные нарушения очень тесно и сложно связаны с органическими изменениями, настолько тесно, что выделить главное порой не представляется возможным.
RANC необходимо применять, как можно шире, потому, что в самом начале любых патологических процессов всё же лежат функциональные расстройства центральной регуляции — нарушение процессов адаптации. Давность заболевания не имеет значения. Расстройство, случившееся хоть месяц назад, хоть пять лет назад, хоть пятнадцать, нужно убирать, так, как всем известно, что эти сбои и расстройства не склонны самостоятельно исчезать со временем, а наоборот «любят» накапливаться.
Как бы ни удивительно всё казалось, но интенсивная стимуляция ретикулярной формации через добавочные нервы (управляющие трапециевидными мышцами) позволяет оказывать воздействие практически на все регуляторные системы (на парасимпатическую часть (за счёт расположения ядер блуждающего нерва в стволе + имеется даже общее, двойное ядро с добавочным нервом), на симпатические подкорковые ядра, на гипофиз-центр гормональной регуляции всех желёз внутренней секреции ну а, кроме того, на дыхательный, сосудодвигательный и температурный центры).
Метод Восстановления Активности Нервных Центров (RANC) не направлен на бесплодные попытки «вылечить симптом». Он направлен на активную перестройку работы всей нервной системы в целом. Лечение позвоночника, суставов, грыжи межпозвоночного диска и седалищного нерва не составляет исключения, так, как лечение не будет эффективно без стимуляции мозга через ретикулярную формацию.
Автором данной методики является доктор Андрей Александрович Пономаренко. Он успешно применяет Метод RANC уже более 20 лет. За это время была создана RANC-Ассоциация врачей, практикующих метод по всей России и даже за её пределами. В настоящее время Андрей Александрович работает в клинике «Неврологика» (г. Краснодар).
Он успешно применяет Метод RANC уже более 20 лет. За это время была создана RANC-Ассоциация врачей, практикующих метод по всей России и даже за её пределами. В настоящее время Андрей Александрович работает в клинике «Неврологика» (г. Краснодар).
Врач невролог «Клиники на Мате Залки» Оксана Валериевна Куликова является участником RANC-Ассоциации и применяет метод RANC в своей работе уже около 5 лет. Поэтому получить консультацию и лечение методом RANC Вы можете в городе Красноярске предварительно записавшись по телефонам 8 (391) 296-56-24 и 8 (391) 252-13-33.
Подробную информацию о методе RANC, авторские статьи Андрея Александровича, а также видео отзывы пациентов Вы сможете найти на сайте клиники «Неврологика» https://nevrologica1.ru/.
Лечение болезни Паркинсона | Medical Tourism with MediGlobus: The best treatment around the world
Доктор Вадим Бережной
General practitioner, Medical expert, Head of the department of medical assistance.
1. Болезнь Паркинсона |
2. Причины патологии |
3. Симптомы заболевания |
4. Лечение методом RANC |
5. Медикаментозная терапия |
6. Операция |
7. Прогнозы |
Время чтения – 13 минут
Что объединяет художника Сальвадора Дали, актера Майкла Джей Фокса, боксера Мохаммеда Али, музыканта Оззи Осборна и Папу Римского Иоанна Павла II? Врачебный диагноз. Все они наряду с ещё 10-ю миллионами людей по всему миру страдают от болезни Паркинсона. Коротко о заболевании и подробно о его сложном лечении — читайте прямо сейчас в новом материале MediGlobus.
Болезнь Паркинсона: причины, симптомы, признаки
Болезнь Паркинсона – это хроническое медленно прогрессирующее заболевание нервной системы, при котором у человека страдают функции движения. Впервые об этой болезни упоминается в 175 году н.э.
Впервые об этой болезни упоминается в 175 году н.э.
Древнеримский врач Гален посвятил ей работу «О дрожании, пульсации, конвульсиях и треморе», в которой описал симптомы заболевания и предполагаемое лечение. Первое исследование болезни провел английский врач Джеймс Паркинсон в 1817 году. Оно легло в основу его «Эссе о дрожательном параличе», а фамилия доктора – в название заболевания.
В наши дни — болезнь Паркинсона является 2-м по распространенности возрастным неврологическим заболеванием после Альцгеймера и одной из самых загадочных патологий. Причины возникновения болезни Паркинсона до сих пор изучаются, а методы лечения совершенствуются.
Чтобы узнать больше информации о диагностике и лечении болезни Паркинсона, оставляйте заявку. Наши координаторы перезвонят Вам и ответят на все вопросы.
Обратиться в MediGlobus
Причины болезни Паркинсона: новое исследование
Согласно американскому порталу Parkinson.org современные исследования сосредоточены на попытке определить и найти гены (или комбинацию генов), которые приводят к болезни Паркинсона. На сегодняшний день обнаружены мутации в 4-х генах, которые напрямую связаны с заболеванием. Исследователи выявили, что эти мутации приводят к гибели дофаминовых нейронов.
На сегодняшний день обнаружены мутации в 4-х генах, которые напрямую связаны с заболеванием. Исследователи выявили, что эти мутации приводят к гибели дофаминовых нейронов.
Дофамин — это не только гормон счастья. Он также является нейромедиатором и отвечает за двигательную активность человека. Потеря 70-80% нейронов, которые высвобождают дофамин, приводит к нарушению движения и дрожи в конечностях.
По информации новостного сайта Рarkinsonsnewstoday от 2 мая 2018 года, в журнале «Neurology» появилось описание последнего исследования заболевания «Mild TBI and risk of Parkinson disease/A Chronic Effects of Neurotrauma Consortium Study».
Его результаты гласят, что черепно-мозговые травмы, в частности, сотрясение мозга, может на 50% увеличить риск возникновения у человека болезни Паркинсона.
Симптомы болезни Паркинсона
Первым симптомом заболевания является дрожь одной руки в состоянии покоя. Человек зачастую не придает значения легкому тремору, списывая его на переутомление, личные переживания, излишнюю эмоциональность.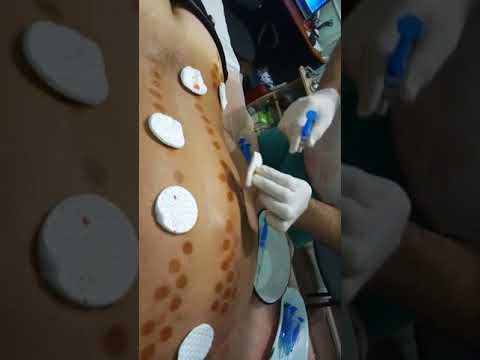
Болезнь Паркинсона развивается медленно, впоследствии начинают дрожать обе руки и голова. Когда человека что-то волнует, тремор становится сильнее, в то время как при обыденных делах он может вовсе сходить на нет.
Признаки болезни Паркинсона
Зачастую заболевание диагностируют у мужчин старше 60-ти лет. Женщин болезнь Паркинсона поражает в 1,5 раза реже. На первых порах недуг протекает практически бессимптомно. По мере развития болезни начинают появляться его явные признаки. Основные признаки болезни Паркинсона:
- медлительность и ограниченность движений: больной может надолго замереть в неудобной позе; шаркающая походка; лицо делается застывшим, безэмоциональным; речь становится тихой, монотонной; повышается тонус мышц: слегка согнутые руки и ноги, сутулость, выдвинутая вперед голова;
- сложность передвижения: человеку трудно начать двигаться и трудно остановиться; тяжело удерживать равновесие; кожа становится жирной, учащается слюноотделение; усиливается потливость, снижается обоняние; появляются запоры, проблемы с мочеиспусканием; полная потеря контроля над телом.

Методы лечения болезни Паркинсона
Борьбы с болезнью Паркинсона подразумевает комплексный подход. Это значит, что для достижения максимально высоких результатов прибегают к нескольким методам лечения. Пациентам назначают специальные лекарства, которые снимают спастичность мышц, улучшают координацию и снижают выраженность тремора.
При прогрессировании недуга больным назначают ультразвуковую терапию или звуковую абляцию МРТ-HIFU. Это безоперационные методики терапии болезни Паркинсона. Ультразвук воздействует на поврежденные участки мозга. Он восстанавливает двигательные функции и смягчает выраженность тремора.
МРТ-HIFU – инновационная методика лечения “дрожания” конечностей при болезни Паркинсона. Данная технология позволяет без хирургического вмешательства “разрушить” пораженные участки мозга, которые отвечают за возникновения тремора. Побочных эффектов нет у 90% пациентов.
Для организации поездки на лечение болезни Паркинсона при помощи безоперационных методов, оставляйте заявку на сайте Медиглобус.
Записаться на терапию
Лечение болезни Паркинсона новым методом RANC
Одним из современных методов лечения этого неврологического заболевания является RANC (The Restoration Of The Activity Of Nerve Centers). Его главная цель — восстановление активности нервных центров. После курса RANC-процедур к пациенту может контролировать собственные движения, дрожь в конечностях становится меньше и в конце концов исчезает.
Автор метода RANC — российский невролог А. А. Пономаренко. Он предполагает, что дофаминовые нейроны (те самые, которые отвечают за двигательные функции человека) не гибнут, а лишь максимально снижают свою активность под воздействием определенных факторов и от этого перестают выполнять свои функции.
Лечение болезни Паркинсона методом RANC предполагает введение больному инъекций 5% АНАЛЬГИНА во все болезненные участки трапециевидных мышц, так как они соответствуют участкам головного мозга с нарушенными функциями.
Короткая боль от процедуры запускает в мозге процесс, который перезапускает работу дофаминовых нейронов и они возобновляют выработку дофамина. Новый RANC метод быстро стал ходовым в лечении болезни Паркинсона в России, так как показывает хорошие результаты за короткий срок — зачастую больным назначают 2-3 процедуры в течение 6 недель.
Новый RANC метод быстро стал ходовым в лечении болезни Паркинсона в России, так как показывает хорошие результаты за короткий срок — зачастую больным назначают 2-3 процедуры в течение 6 недель.
Медикаментозное лечение болезни Паркинсона
Как мы уже говорили, «дрожательный паралич» вызывает нехватка дофамина в головном мозге. Следовательно, лекарственные препараты направлены на имитацию функций этого нейромедиатора. Дофаминергические препараты помогают снизить тонус мышц, улучшить координацию движений, уменьшить тремор головы и конечностей. Наиболее распространенными препаратами для лечения болезни Паркинсона являются:
- Леводопа — первое и самое эффективное средство против паркинсонизма. Действие этого вещества обусловлено его превращением в дофамин прямо в центральной нервной системе, что покрывает его дефицит и впоследствии устраняет симптомы заболевания. Segeline — это ингибитор, который способствует более длительному воздействию дофамина на головной мозг.
 Антихолинерные препараты — блокируют нервные импульсы, которые контролируют движение мышц. Эффективнее всего для пациентов старше 70 лет с сильным тремором и слюнотечением.
Антихолинерные препараты — блокируют нервные импульсы, которые контролируют движение мышц. Эффективнее всего для пациентов старше 70 лет с сильным тремором и слюнотечением.
Хирургическое лечение болезни Паркинсона
Когда заболевание стремительно прогрессирует и больному становится сложно двигаться, разговаривать, работать и жить полноценной жизнью, специалист обсуждает с ним возможность проведения оперативного вмешательства. Наиболее современный хирургический метод лечения болезни Паркинсона — глубокая стимуляция головного мозга (DBS). Процедура предполагает введение в головной мозг специальных электродов, которые создают электрические импульсы.
Стимуляция электрическими импульсами участков головного мозга с нарушенными функциями избавляет пациента от тремора (дрожания конечностей), возвращает ему контроль над телом и эмоциями.
Эту операцию можно пройти в большинстве ведущих медцентров. При этом иностранные пациенты отдают предпочтение таким учреждениям, как: клиника Текнон в Испании, медицинский центр им. Сураски (Ихилов) в Израиле, клиника Лив Хоспитал в Турции, госпиталь при университете СунЧонХян в Южной Корее, университетская клиника Кельна в Германии и т.д.
Сураски (Ихилов) в Израиле, клиника Лив Хоспитал в Турции, госпиталь при университете СунЧонХян в Южной Корее, университетская клиника Кельна в Германии и т.д.
Болезнь Паркинсона — шансы на излечение
Несмотря на существование эффективных современных методов лечения болезни Паркинсона, на сегодняшний день заболевание все еще нельзя вылечить на все 100%. Правильно подобранное лечение позволяет улучшить качество жизни больного, вернуть ему возможность контролировать движения, речь, эмоции.
Помните, болезнь Паркинсона — больше не «дрожательный паралич». Да, это сложное и загадочное неврологическое заболевание. Но оно поддается лечению. Новые методы лечения болезни Паркинсона помогают устранить симптомы недуга на длительное время и вернуть больному радость жизни.
Резюме
Болезнь Паркинсона – неврологическое расстройство, которое развивается в следствие повреждения нейронов головного мозга. Недуг чаще всего диагностируют пожилым пациентам в возрасте от 50-65 лет. Для первоначального лечения болезни Паркинсона назначают медикаментозную терапию. При прогрессировании патологии применяют ультразвуковую терапию, а также радиочастотную абляцию. В качестве хирургического лечения данной патологии применяют глубокую стимуляцию мозга. Медицинские туристы с болезнью Паркинсона обращаются в турецкие, испанские, немецкие и корейские клиники.
Для первоначального лечения болезни Паркинсона назначают медикаментозную терапию. При прогрессировании патологии применяют ультразвуковую терапию, а также радиочастотную абляцию. В качестве хирургического лечения данной патологии применяют глубокую стимуляцию мозга. Медицинские туристы с болезнью Паркинсона обращаются в турецкие, испанские, немецкие и корейские клиники.
Больше информации о лечении болезни Паркинсона за границей можно узнать, обратившись к специалистам нашей компании. Врачи-координаторы ответят на все Ваши вопросы, сориентируют по стоимости и помогут с организацией медицинской поездки. Будьте здоровы — будьте с MediGlobus.
Получить бесплатную консультацию
Источники:
- National Center for Biotechnology Information
- Parkinson.org
- Рarkinsonsnewstoday
Неврология
Доктор Вадим Бережной
General practitioner, Medical expert, Head of the department of medical assistance.
Альбина Головина
Работает в сфере медицинского копирайтинга 2 года. Учится на аспирантуре факультета психологии. Автор нескольких научных публикаций в области клинической психологии. Дополнительно изучает физиологию ЦНС, нейропсихологию и психиатрию. В свободное время изучает практики mindfulness и проводит психологические консультации.
Похожие посты
Насколько эффективно лечение рассеянного склероза стволовыми клетками?
Читать дальше
Рейтинг клиник по лечению болезни Альцгеймера
Читать дальше
ЧТО ТАКОЕ НЕВРИТ ЗРИТЕЛЬНОГО НЕРВА И КАК ЕГО ЛЕЧАТ
Читать дальше
Усредненные по Рейнольдсу уравнения и модели Навье-Стокса (RANS) | Блог системного анализа
Автор Каденс CFDКлючевые выводы
RANS — это численный метод моделирования турбулентного потока, в котором величины потока разлагаются на усредненную по времени и флуктуирующую составляющие (разложение Рейнольдса).

Усреднение уравнений Навье-Стокса дает нелинейный член напряжения Рейнольдса, который требует дополнительного моделирования для полного разрешения системы -> Модель турбулентности.
-
Большинство (если не все) моделей турбулентности RANS основаны на эмпирических наблюдениях.
Турбулентный поток жидкости можно описать с помощью модели Навье-Стокса, усредненной по Рейнольдсу (RANS).
Уравнения Навье-Стокса, возможно, являются одними из самых сложных для использования и решения в математической физике. Этот набор связанных нелинейных уравнений, зависящих от времени, требует множества приближений для достижения аналитических решений, и не все системы разрешимы. Для более общих систем или сложных геометрий необходимы численные методы для решения этих уравнений и получения полезной информации о поведении потока. Некоторые математические аппроксимации могут быть использованы для уменьшения сложности этих уравнений, что поможет ускорить моделирование без потери слишком большой точности.
Некоторые математические аппроксимации могут быть использованы для уменьшения сложности этих уравнений, что поможет ускорить моделирование без потери слишком большой точности.
Усредненные по Рейнольдсу уравнения Навье-Стокса (RANS) представляют собой сокращенную форму общих уравнений Навье-Стокса. В уравнениях RANS стационарное решение отделено от изменяющихся во времени флуктуаций в системе, последние из которых будут учитывать турбулентность в различных режимах течения. Дальнейшие манипуляции с результатами RANS и применение эмпирических моделей турбулентности дают множество других моделей CFD, некоторые из которых нашли свое применение в открытых и коммерческих приложениях CFD.
Обзор усредненных по Рейнольдсу уравнений Навье-Стокса (RANS)
Метод, используемый для получения уравнений RANS, называется разложением Рейнольдса. Усреднение по Рейнольдсу и разложение по Рейнольдсу не относятся непосредственно к манипулированию числом Рейнольдса, а скорее к применению усреднения по времени к уравнениям Навье-Стокса.
С помощью этого разложения можно применить некоторые специализированные операторы и операцию усреднения по времени для получения следующего нелинейного уравнения, описывающего поток (в тензорной записи): RANS) уравнения
Среднее значение тензора скорости деформации определяется по формуле:
0023
Из импульсной части результатов RANS мы видим, что существует нелинейный член, соответствующий напряжению Рейнольдса, эта модель называется моделью напряжения Рейнольдса.
Этот конкретный член может объяснять анизотропную турбулентность, как показано ниже в разделе о турбулентной вязкости. Зависимость этого члена от времени обычно включает в себя средние значения набора нелинейных производных членов. Общая форма этого термина:
Зависимость этого члена от времени обычно включает в себя средние значения набора нелинейных производных членов. Общая форма этого термина:
Зависимость тензора напряжений Рейнольдса от времени в RANS
Хотя потенциально эта модель может быть очень сложной, она также дает некоторую свободу в применении модели к очень конкретным ситуациям, когда определенные члены тензоров деформации и/или напряжения могут быть проигнорировано. Это требует дополнительной модели турбулентности для учета этих нелинейных членов в тензоре напряжений. Большинство этих моделей турбулентности, используемых в уравнениях RANS, определяются на основе эмпирических наблюдений, а не выводятся из первых принципов.
Вихревая вязкость в усредненных по Рейнольдсу уравнениях Навье-Стокса
Для решения уравнений RANS вскоре после их разработки Буссинеск ввел понятие турбулентной вязкости, которое используется для приведения тензора напряжений Рейнольдса к более простой форме. Физически турбулентная вязкость описывает турбулентный перенос энергии посредством движущихся вихревых токов в турбулентном потоке. Математически это связывает напряжение Рейнольдса с турбулентной кинетической энергией, как определено ниже:
Физически турбулентная вязкость описывает турбулентный перенос энергии посредством движущихся вихревых токов в турбулентном потоке. Математически это связывает напряжение Рейнольдса с турбулентной кинетической энергией, как определено ниже:
Константа для условий градиента потока – это вязкость турбулентного вихря (определенная выше как кинематическая вязкость), которая может быть простой константой для вязкого турбулентного потока. Константа пропорциональности для дельта-члена Кронекера представляет собой квадрат скорости потока:
После умножения на плотность в уравнении напряжения Рейнольдса эти члены определяют турбулентную кинетическую энергию, а также анизотропную турбулентность. Эта трактовка применима во многих системах со свободным сдвиговым течением, например, при моделировании слоев смешения, струй, турбулентных пограничных слоев, течений в каналах и многих других задачах.
Модели с одним и двумя уравнениями
Существуют и другие сокращенные модели, являющиеся подмножеством показанной выше модели напряжений Рейнольдса, которые могут иметь одно или два уравнения. В этих разных моделях применяются разные определения, связывающие динамическую турбулентную вязкость с вязкостью объемной жидкости. Эти другие модели также объединяют некоторые члены уравнения напряжения Рейнольдса в компактные определения, как описано ниже:
В этих разных моделях применяются разные определения, связывающие динамическую турбулентную вязкость с вязкостью объемной жидкости. Эти другие модели также объединяют некоторые члены уравнения напряжения Рейнольдса в компактные определения, как описано ниже:
-
- модели k–ε:
- Модели k–ω:
В вышеприведенных определениях скорость рассеяния турбулентности определяется как , а удельная скорость рассеивания определяется как . Разработчикам систем, которым необходимо выполнить моделирование CFD, необходимо будет выбрать подходящую модель, которая соответствует их системе, что требует значительного начального анализа и наблюдений.
Снижение сложности вычислений с помощью инструментов моделирования
Хотя полученные уравнения содержат новый член нелинейного напряжения, который требует дополнительного моделирования, разделение уравнений может уменьшить вычислительную сложность, связанную с учетом турбулентных течений. Пока модель турбулентности может быть разработана для исследуемой системы, поведение данной системы может быть распространено на другие жидкости или геометрические формы. Когда требуется более быстрое вычисление, для оценки потока жидкости в системе можно использовать модель с одним или двумя уравнениями.
Пока модель турбулентности может быть разработана для исследуемой системы, поведение данной системы может быть распространено на другие жидкости или геометрические формы. Когда требуется более быстрое вычисление, для оценки потока жидкости в системе можно использовать модель с одним или двумя уравнениями.
Работать с уравнениями Навье-Стокса, усредненными по Рейнольдсу, или с родственными моделями намного проще, если у вас есть расширенный набор инструментов моделирования CFD. Приложения для создания сетки в Pointwise могут помочь вам создавать точные моделирующие сетки с высоким порядком сетки в сложной геометрии, помогая вам снизить вычислительную сложность без ущерба для точности. Как только сетка создана и готова к дальнейшему анализу, набор инструментов моделирования CFD в Omnis точно и эффективно определит решение потока в вашей системе.
Подпишитесь на нашу рассылку, чтобы получать последние обновления CFD, или просмотрите пакет программного обеспечения Cadence для CFD, чтобы узнать больше о том, какое решение у Cadence есть для вас.
Программное обеспечение CFD Подпишитесь на нашу рассылку новостей
Доступ к электронной книгеСоставная обработка стенок для RANS Расчет сложных турбулентных течений и теплообмена
Составная обработка стенок для RANS Расчет сложных турбулентных течений и теплообмена
Скачать PDF
- Открытый доступ
- Опубликовано:
- М. Поповац 1 и
- К. Ханьялич 1
Течение, турбулентность и горение том 78 , страницы 177–202 (2007 г. )Процитировать эту статью
)Процитировать эту статью
2776 доступов
155 цитирований
Сведения о показателях
Abstract
Мы представляем обобщенное рассмотрение граничных условий на стенке для RANS расчета турбулентных течений и теплообмена. Метод сочетает интегрирование до стенки (ItW) с 90 168 обобщенными пристеночными функциями 90 147 (GWF), которые включают неравновесные эффекты. Граничное условие стены, таким образом, может быть определено независимо от того, находится ли ближайшая к стене точка сетки в пределах вязкого подслоя, в буферной зоне или в полностью турбулентной области. Расчеты с мелкими и крупными сетками стационарного и пульсирующего течения в плоском канале, течении за обратным уступом и в круглой набегающей струе с использованием предложенной составная обработка стенок (CWT) удовлетворительно согласуются с имеющимися экспериментами и данными DNS. Этот метод рекомендуется для расчетов промышленных потоков в сложных областях, где трудно создать расчетную сетку, которая априори удовлетворяла бы требованиям ИВ или ВФ.
Расчеты с мелкими и крупными сетками стационарного и пульсирующего течения в плоском канале, течении за обратным уступом и в круглой набегающей струе с использованием предложенной составная обработка стенок (CWT) удовлетворительно согласуются с имеющимися экспериментами и данными DNS. Этот метод рекомендуется для расчетов промышленных потоков в сложных областях, где трудно создать расчетную сетку, которая априори удовлетворяла бы требованиям ИВ или ВФ.
Скачайте, чтобы прочитать полный текст статьи
Ссылки
Чиенг, К.С., Лаундер, Б.Е.: Расчет турбулентного переноса тепла после резкого расширения трубы. Число. Теплопередача. 3 , 189–207 (1980)
АДС Google ученый
Крафт, Т.Дж., Герасимов, А.В., Яковидес, Х., Лаундер, Б.Э.: Прогресс в обобщении методов лечения стеночной функции.
 Междунар. J. Heat Fluid Flow 23 , 148–160 (2002)
Междунар. J. Heat Fluid Flow 23 , 148–160 (2002)Статья Google ученый
Jayatilleke, C.L.V.: Влияние числа Прандтля и шероховатости поверхности на сопротивление ламинарного подслоя передаче импульса и тепла. прог. Тепломассообмен. 1 , 193 (1969)
Google ученый
Эш, Т., Ментер, Ф.Р.: Прогнозы теплообмена на основе двухпараметрических моделей турбулентности с усовершенствованной обработкой стенок. Турбул. Тепломассообмен. 4 , 633–640 (2003)
Google ученый
Калицын Г., Медик Г., Яккарино Г., Дурбин П.: Пристеночное поведение моделей турбулентности RANS и последствия для пристеночных функций. Дж. Вычисл. физ. 204 , 265–291 (2005)
Статья МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google ученый
«>Кадер, Б.А.: Профили температуры и концентрации в полностью турбулентных пограничных слоях. Междунар. J. Тепломассоперенос 24 , 1541–1544 (1981)
Артикул Google ученый
Ханьялич, К., Поповац, М., Хадзиабдич, М.: Надежная модель вихревой вязкостной турбулентности при эллиптической релаксации у стенки для CFD. Междунар. J. Heat Fluid Flow 25 , 1047–1051 (2004)
Статья Google ученый
Дурбин, П.А.: Моделирование замыкания пристеночной турбулентности без «функций демпфирования». Теор. вычисл. Динамик жидкости 3 , 1–13 (1991)
МАТЕМАТИКА Google ученый
«>Лоуренс Д.Р., Урибе Дж.К., Утюжников С.В.: Надежная формулировка модели v2-f. Поток Турбул. Сгорел. 73 , 169–185 (2005)
Статья Google ученый
Ханьялич, К., Лоуренс, Д., Поповац, М., Урибе, К.: ( v 2/ k – f ) модель турбулентности и ее применение к вынужденной и естественной конвекции. В: Роди, В., Мулас, М. (ред.) Инженерное моделирование турбулентности и эксперименты, том. 6, стр. 67–76. Эльзевир, Амстердам, Нидерланды (2005)
Google ученый
Дурбин П.
 А.: О критической аномалии k — ε . Междунар. J. Heat Fluid Flow 17 , 89–90 (1996)
А.: О критической аномалии k — ε . Междунар. J. Heat Fluid Flow 17 , 89–90 (1996)Статья Google ученый
Нг, Э.Ю.К., Тан, Х.Ю., Лим, Х.Н., Чой, Д.: Пристеночная функция для моделей закрытия турбулентности. вычисл. мех. 29 , 178–181 (2002)
Статья МАТЕМАТИКА Google ученый
Поповац, М.: к.м.н. диссертация, Делфтский технологический университет, Делфт, Нидерланды (2006 г.)
Райхардт, Х.: Vollstaendige Darstellung der turbulenten Geschwindigkeitsverteilung in glatten Leitungen. ЗАММ 31 , 208–219 (1951)
МАТЕМАТИКА Google ученый
Spalding, D.B.: Единая формула закона стены. ASME J. Appl. мех. 28 , 444–458 (1961)
Google ученый
«>Лиакопулос, А.: Явное представление полного профиля скорости в турбулентном пограничном слое. AIAA J. 22 , 844–846 (1984)
Артикул ОБЪЯВЛЕНИЯ Google ученый
Ши, Т., Повинелли, Л., Лю, Н.: Применение обобщенных пристеночных функций для сложных турбулентных течений. В: Роди, В., Фуэйо, Н. (ред.) Инженерное моделирование турбулентности и эксперименты, том. 5, стр. 177–186. Эльзевир, Амстердам, Нидерланды (2002)
Google ученый
Танахаси, М., Канг, С.-Дж., Миямото, С., Сиокава, С., Мияучи, Т.: Масштабный закон мелкомасштабных вихрей в турбулентных русловых течениях до Ре т =800.
 Междунар. J. Heat Fluid Flow 25 , 331–340 (2004)
Междунар. J. Heat Fluid Flow 25 , 331–340 (2004)Статья Google ученый
Бромер, А., Меринг, Дж., Шайдер, Дж., Басара, Б., Тачль, Р., Ханайлич, К., Поповац, М.: Прогресс в 3D-CFD-расчете газовых и теплопередача со стороны воды в двигателях внутреннего сгорания. В: Eichlseder, H. (ed.) 10. Tagung der Arbeitsprozess der Verbrebubgsmotors, Технический университет Граца, Австрия, 22–23 сентября 2005 г.
Купер, Д., Джексон, Д.К., Лаундер, Б.Е., Ляо, Г.Х.: Исследования ударной струи для оценки модели турбулентности – I. Эксперименты с потоком. Междунар. J. Тепломассообмен 36 , 2675–2684 (1993)
Статья Google ученый
Скотти, А., Пиомелли, У.: Численное моделирование пульсирующего турбулентного течения в канале. физ. Жидкости 13 , 1367–1384 (2001)
Артикул ОБЪЯВЛЕНИЯ Google ученый
«>Baughn, J., Shimizu, S.: Измерения теплопередачи от поверхности с однородным тепловым потоком и падающей струей. ASME J. Теплопередача 111 , 1096–1098 (1989)
Google ученый
Baughn, J., Hechanova, W.E., Yan, X.: Экспериментальное исследование влияния увлечения на передачу тепла от плоской поверхности к нагретой круглой падающей струе. ASME J. Heat Transfer 113 , 1023–1025 (1991)
Статья Google ученый
Тачль, Р., Басара, Б., Шнайдер, Дж., Ханьялич, К., Поповац, М., Бромер, А., Меринг, Дж.: Усовершенствованное моделирование турбулентного теплообмена для двигателей внутреннего сгорания с использованием АВЛ ПОЖАР.
 В: Междунар. Многомерное моделирование двигателей, собрание группы пользователей, Детройт, Мичиган, 2 апреля 2006 г.
В: Междунар. Многомерное моделирование двигателей, собрание группы пользователей, Детройт, Мичиган, 2 апреля 2006 г.
Крафт, Т.Дж., Гант, С.Е., Яковидес, Х., Лаундер, Б.Э.: Новая стратегия пристеночной функции для сложных турбулентных течений. Число. Теплопередача, часть B 45 , 301–317 (2004)
Google ученый
Специале, К.Г., Саркар, С., Гацки, Т.: Моделирование корреляции давления и деформации турбулентности: подход к динамике инвариантной системы. Дж. Жидкостная механика. 227 , 245–272 (1991)
Статья МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google ученый
Маскер, А.Дж.: Явное выражение для распределения скорости гладкой стенки в турбулентном пограничном слое. AIAA J. 17 , 655–657 (1979)
МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google ученый
Vogel, J.C., Eaton, J.K.: Комбинированные измерения теплопередачи и гидродинамики после обратной ступени. ASME J. Heat Transfer 107 , 922–929 (1985)
Статья Google ученый
Ссылки на скачивание
Информация об авторе
Авторы и организации
Кафедра многомасштабной физики, Факультет прикладных наук, Делфтский технологический университет, Лоренцвег 1, 2627 MJ, Делфт10
Нидерланды Popovac & K. Hanjalic
Авторы
- M. Popovac
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Академия
- K. Hanjalic
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Автор, ответственный за корреспонденцию
М. Поповац.
Права и разрешения
Открытый доступ Это статья с открытым доступом, распространяемая в соответствии с условиями некоммерческой лицензии Creative Commons Attribution (
https://creativecommons.

 Междунар. J. Heat Fluid Flow 23 , 148–160 (2002)
Междунар. J. Heat Fluid Flow 23 , 148–160 (2002)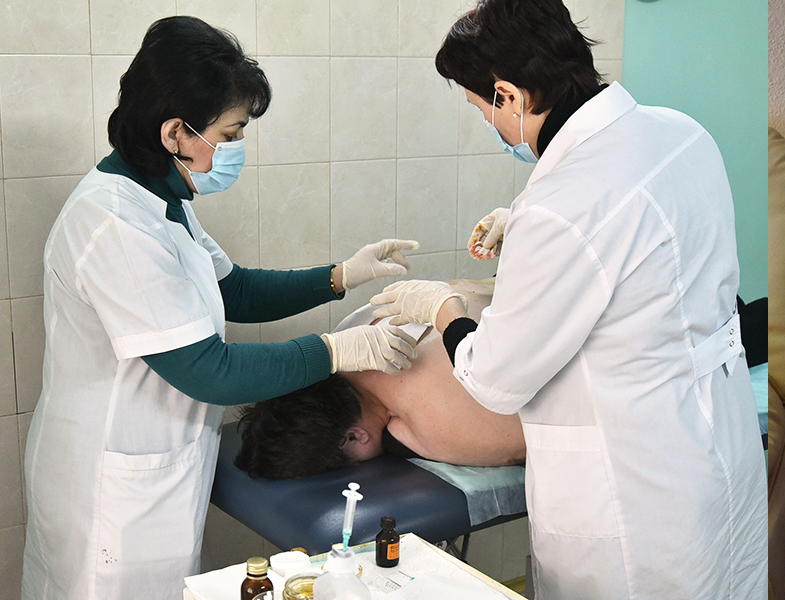 А.: О критической аномалии k — ε . Междунар. J. Heat Fluid Flow 17 , 89–90 (1996)
А.: О критической аномалии k — ε . Междунар. J. Heat Fluid Flow 17 , 89–90 (1996) Междунар. J. Heat Fluid Flow 25 , 331–340 (2004)
Междунар. J. Heat Fluid Flow 25 , 331–340 (2004) В: Междунар. Многомерное моделирование двигателей, собрание группы пользователей, Детройт, Мичиган, 2 апреля 2006 г.
В: Междунар. Многомерное моделирование двигателей, собрание группы пользователей, Детройт, Мичиган, 2 апреля 2006 г.