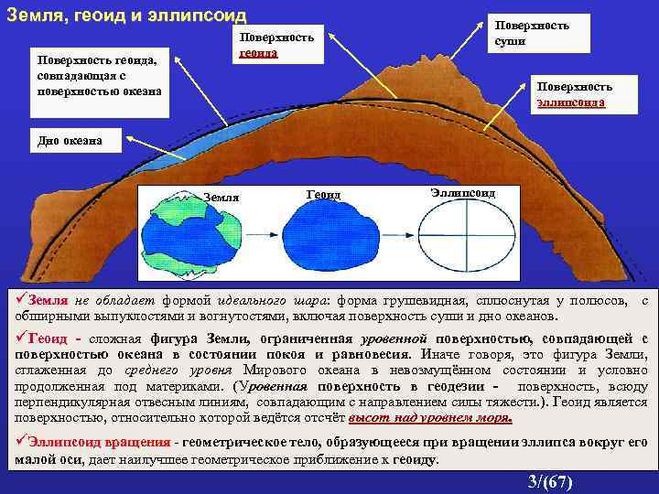
Какая на самом деле форма Земли?
Если вы думаете, что наша планета имеет форму шара, то вы ошибаетесь.
Grazia
Теги:
Evergreen
Приобретают такую форму и каменистые объекты, имеющие, по очень грубым оценкам, хотя бы 600 км в поперечнике и массу как минимум 0,01% от массы нашей планеты. Но дальше начинаются детали и тонкости.
Что влияет на форму небесного тела
Форму планеты Земля определяет несколько факторов. Во-первых, вращение шара Земли создает центробежную силу, причем на экваторе она выше, чем у полюсов. Из-за этой разницы планета оказывается чуть сплюснута и ее диаметр, проходящий через экватор, становится на 43 км больше. Если бы всю ее целиком покрывал бескрайний океан, то он образовывал бы чуть вытянутый эллипсоид, и эта фигура более точно соответствует действительной форме Земли.
Эта 3D-модель истинной формы Земли была подготовлена американскими учёными.
Масса распределена по поверхности нашей планеты не совсем равномерно. Как правило, литосферные плиты материков толще, чем океанические. Высокие горы и глубокие впадины, мощные рудные отложения – все это создает слабые аномалии, участки, в которых гравитационное поле оказывается чуть сильнее или слабее обычного. Гравитационные аномалии обнаруживают по их влиянию на высоту полета спутников, работающих на околоземной орбите. Например, два одинаковых зонда миссии GRACE облетали планету около 15 лет, проходя над каждым участком поверхности раз в месяц и с ювелирной точностью отслеживая расстояние друг до друга. Пролет над любой гравитационной аномалией вызывал небольшие изменения их положения, и собранные при этом данные позволили составить самую детальную карту гравитационного поля Земли и уточнить ее форму.
Так какая же форма у Земли на самом деле?
Такая поверхность называется геоидом — это и есть настоящая форма Земли: в отличие от ровного эллипсоида, его высота в каждом участке определяется точным балансом между центробежной силой и локальной гравитацией.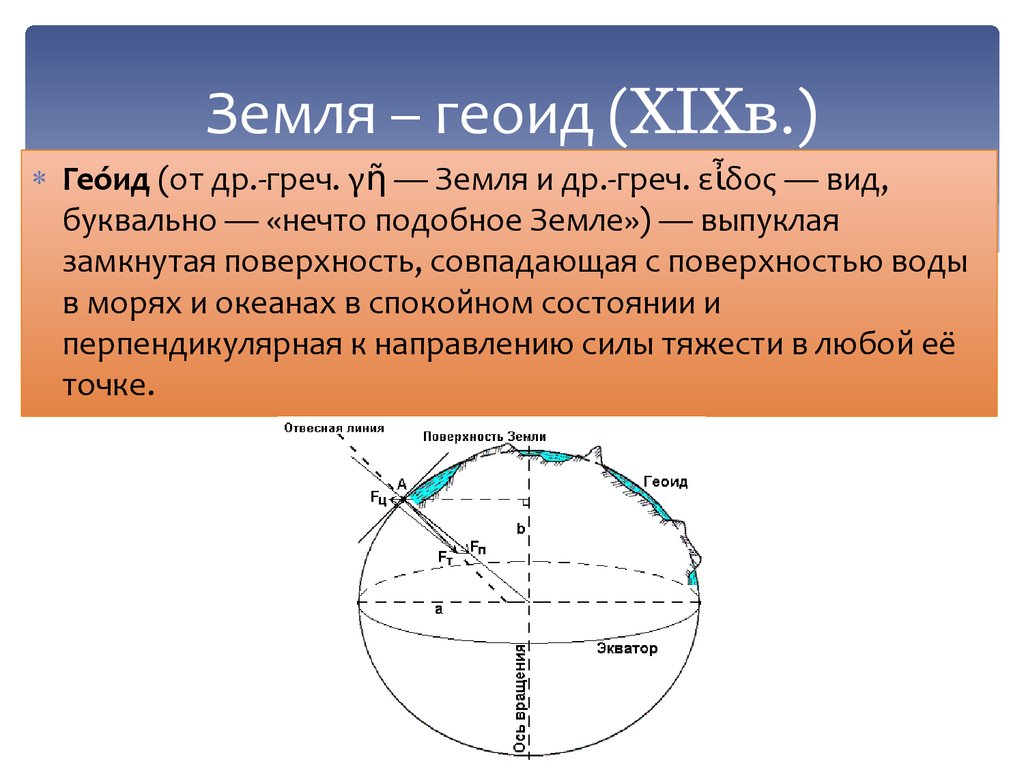
Гравитация сильно влияет на движение литосферных плит, а потому настоящая форма Земли не идеальный эллипсоид, а геоид.
На фоне размеров всей планеты Земля даже самые крупные детали ее поверхности покажутся совсем крошечными. Например, для Бездны Челленджера (10,9 км ниже уровня моря) отклонение от среднего радиуса Земли составляет всего 0,17%, а для Джомолунгмы (8,8 км) – 0,14%. Тем более незаметны будут аномалии реальной формы Земли — геоида: от эллипса его поверхность отклоняется в пределах от –85 до 106 м. Поэтому 3D-модель, подготовленная учеными американского Национального управления океанических и атмосферных исследований (NOAA), усилена: аномалии на ней дополнительно выделены. Однако в остальном она полностью опирается на данные GRACE и наглядно демонстрирует непростую форму нашей в целом круглой планеты.
Источник: Популярная Механика
как доказать что земля имеет форму эллипса? помогите пожалуйста! — Спрашивалка
как доказать что земля имеет форму эллипса? помогите пожалуйста! — СпрашивалкаАЗ
Андрей Загребаев
- форма
- земля
- эллипс
АА
Александра Азеева
Эллипс — фигура плоская.
Так что далее придётся доказывать, что Земля стоит на трёх китах или на чём-то ещё лежит.
НА
Наталья Алексина
Земля не имеет форму эллипса. Она имеет форму геоида.
Наталья Торгачева
ну она ее не имеет)
ЕЯ
Екатерина Яковлева
Земля приплюснута у полюсов-мой ответ
А вот что говорит Википедия-Форма Земли (геоид) близка к сплюснутому эллипсоиду. Расстояние точек геоида, до точек аппроксимирующего его эллипсоида составляет до 100 метров. Средний диаметр планеты примерно равен 12 742 км. Это приблизительно 40 000 км/, так как метр в прошлом определялся, как 1/10 000 000 расстояния от экватора до северного полюса через Париж (из-за неправильного учёта полюсного сжатия Земли эталон метра 1795 года оказался короче приблизительно на 0,2 мм, отсюда неточность) .
Вращение Земли создаёт экваториальную выпуклость, поэтому экваториальный диаметр на 43 км больше, чем диаметр между полюсами планеты.
Высшей точкой твёрдой поверхности Земли является гора Эверест (8848 м над уровнем моря) , а глубочайшей — Марианская впадина (11 022 м под уровнем моря) . Поэтому, по сравнению с идеальным эллипсоидом, Земля имеет допуск в пределах 0,17 % (1/584), что меньше 0,22 % — допустимого допуска для бильярдного шара. Из-за выпуклости экватора, самой удалённой точкой поверхности от центра Земли фактически является вершина вулкана Чимборасо в Эквадоре
ЛД
Людмила Дозорцева
Кто тебе сказал такую глупость?
АФ
Анна Фомина
эллипс — это линия, Земля тело имеющее форму ГЕОИДА или приблизительно эллипсоида, т. е. шара сплюснутого у полюсов, а доказать просто — сравнить диаметр по экватору с диаметром по полюсам!
Annet
Врöде обсуждали тут уже, юзай — windowsfix
Искандар Акбаров
Люди а эллипс и геоид это одно и тоже!!!
В нулевом приближении можно считать, что Земля имеет форму шара со средним радиусом 6371,3 км.
Похожие вопросы
Какую форму имеет земля? Как это можно доказать. Как это можно доказать.
помогите, пожалуйста, доказать!
Кто доказал, что Земля имеет форму шара? Помогите пожалуйста!
Как доказать учителю физики что земля имеет форму шара, а не шайбы как он говорит?
какую форму имеет земля
Пожалуйста помогите доказать
Какую форму имеет земля? (ниикогда не угодаете)
Почему говорят «круг эллиптической формы»? Если круг по своей форме отнюдь не может быть эллипсом.
Как доказали, что в земле есть ядро?
Планета земля имеет форму : а) эллипса; б) эллипсоида; в) овала; помогите пожалуйста
Эллипсоиды
Эллипсоид — это трехмерная фигура, все плоские сечения которой представляют собой либо эллипсы, либо окружности.
Эллипсоид имеет три оси, которые пересекаются в центре эллипсоида. Каждая ось перпендикулярна двум другим, и эллипсоид симметричен относительно всех трех осей. Эллипсоид часто описывают как трехмерный аналог эллипса. На диаграмме ниже вы можете увидеть общий ( трехосный ) эллипсоид с полуосями a , b и c .
У эллипсоида три взаимно перпендикулярные оси
Существует четыре различных типа эллипсоидов, каждый из которых характеризуется особым соотношением между полуосями a , b и c с точки зрения их относительных длин:
- а > б > в — общий или трехосный эллипсоид
- а = b > с — сплюснутый эллипсоид вращения (или сплюснутый сфероид)
- a = b < c — вытянутый эллипсоид вращения (или вытянутый сфероид)
- a = b = c — сфера (часто называемая вырожденным случаем)
На самом деле нас здесь не интересует сфера.
Это рассматривается на странице под названием «Сфера» в этом разделе. Сплюснутые и вытянутые сфероиды здесь также не представляют для нас большого интереса. Они являются предметом страницы под названием «Сфероиды». Термин «эллипсоид» чаще всего используется для обозначения общий (или трехосный ) эллипсоид, у которого полуоси a , b и c имеют разную длину. Полуось
Пляжная галька часто представляет собой трехосные эллипсоиды.
Формула объема трехосного эллипсоида аналогична формуле объема сферы, за исключением того, что вместо одного радиуса мы должны рассматривать три отдельные полуоси:
| В = | 4 | π abc |
| 3 |
Достаточно сказать, что полная формула площади поверхности трехосного эллипсоида включает в себя члены типа неполных эллиптических интегралов первого и второго рода , которые столь же неприятны, как и звучат. Требуемые вычисления включают в себя интеграцию (один из основных элементов в области математики, известной как исчисление ), и как таковые несколько выходят за рамки этой страницы. Разумное приближение площади поверхности трехосного эллипсоида может можно получить с помощью следующей формулы, впервые предложенной в 2004 году датским геологом Кнудом Томсеном:| A ≈ 4π | a p b p + a p c p + b p c p | 1/стр |
| 3 |
где значение 1,6075 для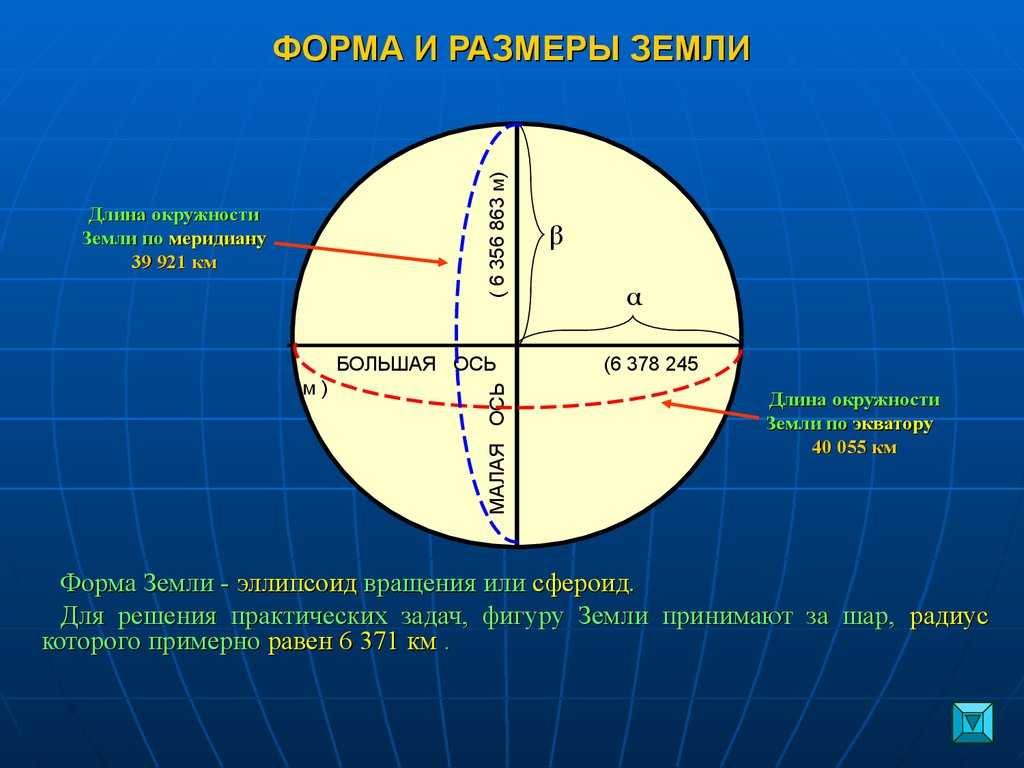 
Сфероиды и сферы—ArcMap | Документация
- Определение сфероида
- Определение различных сфероидов для точного картирования
Форма и размер поверхности географической системы координат определяется сферой или сфероидом. Хотя Землю лучше всего изображать в виде сфероида, иногда ее рассматривают как сферу, чтобы упростить математические вычисления. Предположение о том, что Земля является сферой, возможно для карт мелкого масштаба (менее 1:5 000 000). В этом масштабе разница между сферой и сфероидом не заметна на карте. Однако для обеспечения точности крупномасштабных карт (масштаб 1:1 000 000 или больше) сфероид необходим для представления формы Земли. Между этими масштабами выбор использования сферы или сфероида будет зависеть от цели карты и точности данных.
Определение сфероида
Сфера основана на окружности, а сфероид (или эллипсоид) основан на эллипсе.
Сфероид или эллипсоид — это сфера, сплющенная у полюсов.
Форма эллипса определяется двумя радиусами. Больший радиус называется большой полуосью, а меньший радиус – малой полуосью.
Большая полуось или экваториальный радиус составляет половину большой оси. малая полуось или полярный радиус составляет половину малой оси.Вращение эллипса вокруг малой полуоси создает сфероид. Сфероид также известен как сплюснутый эллипсоид вращения. На следующем рисунке показаны большая и малая полуоси сфероида.
Большая полуось лежит в экваториальной плоскости, а малая полуось перпендикулярна экваториальной плоскости.Сфероид определяется либо большой полуосью а и малой полуосью b, либо а и уплощением. Уплощение представляет собой разницу в длине между двумя осями, выраженную в виде дроби или десятичной дроби. Сглаживание f получается следующим образом:
f = (a - b) / a
Сглаживание представляет собой небольшое значение, поэтому вместо него обычно используется величина 1/f. Это параметры сфероида для Мировой геодезической системы 1984 (WGS 1984 или WGS84):
а = 6378137,0 метров б = 6356752,31424 метра 1/f = 298,257223563
Диапазон выравнивания от 0 до 1.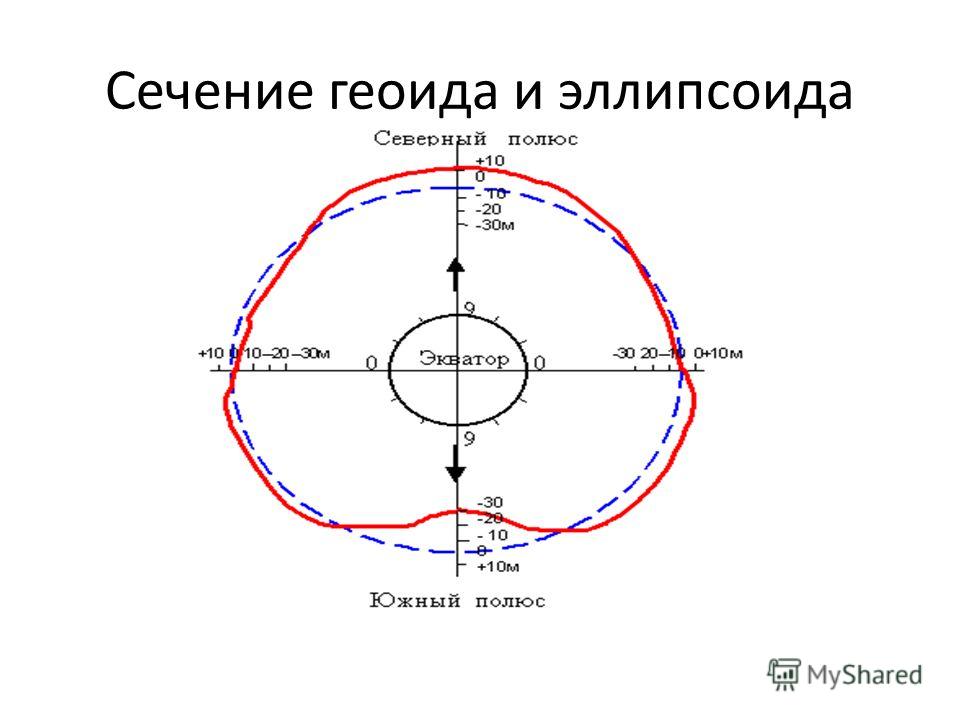
Значение выравнивания 0 означает, что две оси равны, в результате чего получается сфера. Сплющивание Земли составляет примерно 0,003353. Другая величина, которая, как и уплощение, описывает форму сфероида, — это квадрат эксцентриситета, e 2 . Он представлен следующим образом:
Определение различных сфероидов для точного картирования
Земля исследовалась много раз, чтобы лучше понять особенности ее поверхности и ее характерные неровности. В результате исследований было получено множество сфероидов, представляющих Землю. Как правило, сфероид выбирается, чтобы соответствовать одной стране или определенной области. Сфероид, который лучше всего подходит для одной области, не обязательно подходит для другой области. До недавнего времени в североамериканских данных использовался сфероид, определенный Кларком в 1866 году. Большая полуось сфероида Кларка 1866 года составляет 6 378 206,4 метра, а малая полуось — 6 356 583,8 метра.
Из-за вариаций гравитации и характеристик поверхности Земля не является ни идеальной сферой, ни идеальным сфероидом.